Kendall tau是用來度量關(guān)聯(lián)關(guān)系的。
(引自wikipedia:http://en.wikipedia.org/wiki/Kendall_tau_rank_correlation_coefficient)
==============================================
Let (x1, y1), (x2, y2), …, (xn, yn) be a set of joint observations from two random variables X and Y respectively, such that all the values of (xi) and (yi) are unique. Any pair of observations (xi, yi) and (xj, yj) are said to be concordant if the ranks for both elements agree: that is, if both xi > xj and yi > yj or if both xi < xj and yi < yj. They are said to be discordant, if xi > xj and yi < yj or if xi < xj and yi > yj. If xi = xj or yi = yj, the pair is neither concordant nor discordant.
The Kendall τ coefficient is defined as:
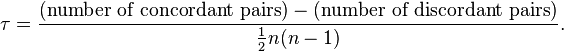
=========================================================
同一篇文章繼續(xù)引用關(guān)于ties:
=========================================================
A pair {(xi, yi), (xj, yj)} is said to be tied if xi = xj or yi = yj; a tied pair is neither concordant nor discordant. When tied pairs arise in the data, the coefficient may be modified in a number of ways to keep it in the range [-1, 1]:
Tau-b statistic, unlike tau-a, makes adjustments for ties and is suitable for square tables. Values of tau-b range from ?1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association.
The Kendall tau-b coefficient is defined as:

where

================================================
靠,搞了半天才理解,上面公式中所謂nc, nd里面的c和d,指的是concordant和discordant.
在sas中計算Kendall tau-2比較簡單,直接用proc freq就行,原來proc freq如此強(qiáng)大啊。
sas程序舉例:
data color;
input Region Eyes $ Hair $ Count @@;
label Eyes ='Eye Color'
Hair ='Hair Color'
Region='Geographic Region';
datalines;
1 blue fair 23 1 blue red 7 1 blue medium 24
1 blue dark 11 1 green fair 19 1 green red 7
1 green medium 18 1 green dark 14 1 brown fair 34
1 brown red 5 1 brown medium 41 1 brown dark 40
1 brown black 3 2 blue fair 46 2 blue red 21
2 blue medium 44 2 blue dark 40 2 blue black 6
2 green fair 50 2 green red 31 2 green medium 37
2 green dark 23 2 brown fair 56 2 brown red 42
2 brown medium 53 2 brown dark 54 2 brown black 13
;
proc freq data = color noprint ;
tables eyes*hair / measures noprint ;
weight count;
output out=output KENTB;
test KENTB;
run;
另外跟Kendall tau有點兒關(guān)聯(lián)的是Somer’s D,但是搜索了一下沒看到公式,反正Somer’s D也可以用sas proc freq直接算,方法類似。
Somers' D(C|R) and Somers' D(R|C) are asymmetric modifications of tau-b.Somers' D differs from tau-b in that it uses a correction only for pairs that are tied on the independent variable.