人在江湖

一，基礎(chǔ)概念：

Probability of default(PD)：PD是巴塞爾協(xié)議中一個重要的參數(shù)，它用來計算某個客戶或某批具有相似特征的客戶貸款不還的概率。

Hosmer–Lemeshow test：PD中眾多統(tǒng)計檢驗的其中一種，評估預(yù)測值與實際值在各個分組（subgroup, pool, bin）中擬合程度。

自由度：自由度是指隨機變量中所含獨立隨機變量的個數(shù)n．如果這些獨立隨機變量受到k個約束條件的限制，那么自由度就變?yōu)?i>n-k．

概率密度函數(shù)：是一個描述這個隨機變量的輸出值在某一個確定的取值點附近的可能性的函數(shù)。

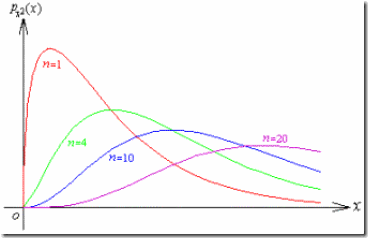
卡方（χ²）分布：

設(shè)X₁, X₂,…,X_n是相互獨立的隨機變量且均服從標(biāo)準正態(tài)分布N(0，1)，則隨機變量

                    χ²= X₁²+X₂²+…+X_n

的分布稱為服從自由度為n的χ²分布，記為χ²～χ²(n)

卡方分布的密度函數(shù)圖為：

二， Hosmer–Lemeshow test的使用方法

Hosmer–Lemeshow test 的統(tǒng)計量是:

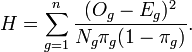
這里 O_g, E_g, N_g, and π_g 示觀察到的事件，預(yù)期的事件，觀察數(shù), 預(yù)測的第g^th組的風(fēng)險（在PD模型中，）， n是組數(shù). 這個統(tǒng)計量符合自由度為n-2或n的卡方分布。

其他統(tǒng)計量都很直白，解釋一下E_g的計算：實際應(yīng)用中，可以用當(dāng)前分組的違約概率 x 當(dāng)前分組的觀測值數(shù)目。

有了統(tǒng)計量的值之后，下一步計算就要依靠“這個統(tǒng)計量符合自由度為n-2或n的卡方分布”了。那么什么時候用自由度為n，什么時候用自由度為n-2呢。在書Basel2 risk parameters里有這樣一段解釋在321頁。這本書可以在我的skydrive里找到https://skydrive.live.com/?cid=D8B11F9BF86FECFA&id=D8B11F9BF86FECFA%211346&sc=documents#：

“When using the HSLS statistic as a measure of fit in the process of model finding, then
we say “in-sample”, because the model estimation sample and the sample on which the
measure of fit is computed are identically. In this case the distribution is F2 with G 2
degrees  of  freedom.  When  using  the  HSLS  statistic  for  backtesting,  we  say  “out-of-
sample”,  because  there  is  no  observation  coexistent  in  the  estimation  sample  and  the
validation sample. ”

如果理解沒錯的話，在建模驗證階段，自由度是n-2, 模型建好之后，自由度都是n。

卡方檢驗P值的計算方式是1 - 特定自由度下卡方的的CDF，詳見wikipedia：http://en.wikipedia.org/wiki/Chi-square_distribution中Table of χ² value vs P value部分

CDF指的是Cumulative distribution function，就是分布函數(shù)，詳見wikipedia: http://en.wikipedia.org/wiki/Cumulative_distribution_function