分類問題使用決策樹有一些好處，比如不需要太多domain知識。Learning和分類的過程也比較快。
決策樹的算法需要三個參數：被分類的對象， 對象的屬性列表， 屬性的選擇算法(attribute_selection_method)，學習決策樹，主要是學習屬性選擇算法。
Data Mining Concepts and Techniques書里對決策樹的構建過程闡述的很清晰，書可以在之前的博客找到： http://www.tkk7.com/vcycyv/archive/2011/09/05/357967.html
(1) create a node N;
(2) if tuples in D are all of the same class, C then
(3) return N as a leaf node labeled with the class C;
(4) if attribute list is empty then
(5) return N as a leaf node labeled with the majority class in D; // majority voting
(6) apply Attribute selection method(D, attribute list) to ?nd the “best” splitting criterion;
(7) label node N with splitting criterion;
(8) if splitting attribute is discrete-valued and
multiway splits allowed then // not restricted to binary trees
(9) attribute list = attribute list - splitting attribute; // remove splitting attribute
(10) for each outcome j of splitting criterion
// partition the tuples and grow subtrees for each partition
(11) let D j be the set of data tuples in D satisfying outcome j; // a partition
(12) if D j is empty then
(13) attach a leaf labeled with the majority class in D to node N;
(14) else attach the node returned by Generate decision tree(D j , attribute list) to node N;
endfor
(15) return N;
生成的樹是否是binary的主要取決于屬性的選擇算法(attribute_selection_method)，比如gini index算法生成的tree就是binary的，information gain生成的沒有這樣的限制。
關于算法：
information gain:
給對象集合D的某一個對象分組所需要的information可以這樣算：
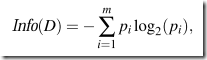
其中Pi代表任一對象屬于類別Ci的概率
如果用某個屬性A來分D,經過A把D分成幾組之后，給某一個對象分組所需要的information表述如下（看不懂沒關系，下面有例子）
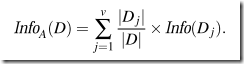
information gain就可以這樣算：
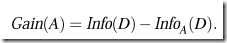
例子：
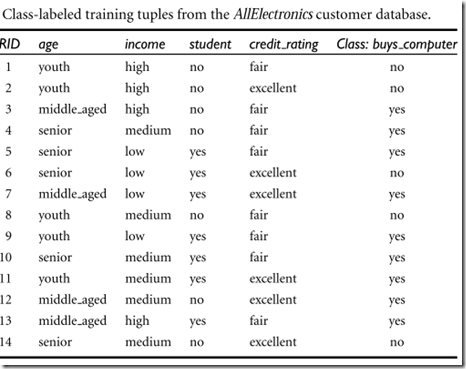
The class label attribute, buys computer, has two distinct values (namely, {yes, no}); therefore, there are two distinct
classes (that is, m = 2). Let class C1 correspond to yes and class C2 correspond to no.There are nine tuples of class yes and ?ve tuples of class no. A (root) node N is createdfor the tuples in D. To ?nd the splitting criterion for these tuples, we must compute the information gain of each attribute. We ?rst compute the expected information needed to classify a tuple in D:
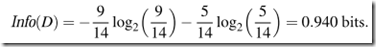
Next, we need to compute the expected information requirement for each attribute. Let’s start with the attribute age. We need to look at the distribution of yes and no tuples for each category of age. For the age category youth, there are two yes tuples and three no tuples. For the category middle aged, there are four yes tuples and zero no tuples. For the category senior, there are three yes tuples and two no tuples.
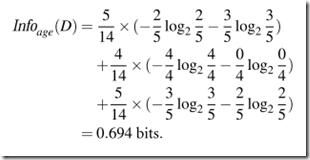
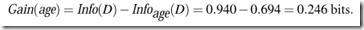
Similarly, we can compute Gain(income) = 0.029 bits, Gain(student) = 0.151 bits, and Gain(credit rating) = 0.048 bits. Because age has the highest information gain among the attributes, it is selected as the splitting attribute.
Gain ratio簡述：
information gain在處理多值屬性的時候效果不好，比如如果有一個屬性是product_id,那么經過他分所有對象之后，每個對象自成一組，也就是說每個組都是pure的，所以分組后的info（D）就是0，所以用product_id分組自然gain的值最大，但是顯然這樣分組沒意義。Gain ratio相當于調整了information gain, 它用比值來計算而不是減法。具體在書里有例子，不詳述。
Gini index:
Gini index是用來算impurity of D的。上面說過，這種算法是binary split的。舉個binary split的例子：
if income has three possible values, namely {low,
medium, high}, then the possible subsets are {low, medium, high}, {low, medium}, {low,high}, {medium, high}, {low}, {medium}, {high}, and {}. We exclude the power set,{low, medium, high}, and the empty set from consideration since, conceptually, they do not represent a split.
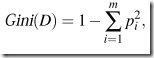
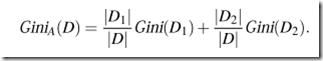
示例：
there are nine tuples belonging to the class buys computer = yes and the remaining ?ve tuples belong to the class buys computer = no.
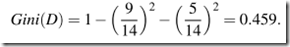
To ?nd the splitting criterion for the tuples in D, we need to compute the gini index for each attribute. Let’s start with the attribute income and consider each of the possible splitting subsets. Consider the subset {low, medium}. This would result in 10 tuples in partition D1 satisfying the condition “income 屬于{low, medium}.” The remaining four tuples of D would be assigned to partition D2 . The Gini index value computed based on this partitioning is
類似地可以算出來其他Income的subset, 在擴展到可以類似算age 之類的attribute。
關于Prune：
為了去掉噪音和outlier,需要修剪(prune) tree.有兩種修剪方法：preprune和postprune.
preprune就是一邊split tree，一邊算著統計量，比如information gain, 或者gini index之類的，一旦算出來的值夠不到threshold,就停下來變成葉子節點。
postprune就是把tree grow完了之后，再從底向上剪掉一些分支。剪掉分支的算法叫cost complexity, 它主要基于Leaf的個數和error rate. 就是算一個node如果prune它和保留它之間哪個cost complexisty更大，如果prune之后cost complexity更小了，就prune它。注意算cost complexity要基于一個單獨的data set, 不用training dataset, 也不用validation data set.
往往認為postprune可靠性更好一些。 實際中，preprune和postprune可以結合在一起使用。
Data Mining techniques for Marketing Sales and Customer Relationship Management這本書提出了兩個需要注意的地方：
1. 經過某次split之后的生成兩個leaf節點，他們可能是同一個category的。只是概率不一樣，但是都過了threshold.
2. binary tree可以分target是多個category的。反過來，多值tree也可以給binary target的分類。