上節(jié)說到我們有了一個(gè)線性分類函數(shù)，也有了判斷解優(yōu)劣的標(biāo)準(zhǔn)——即有了優(yōu)化的目標(biāo)，這個(gè)目標(biāo)就是最大化幾何間隔，但是看過一些關(guān)于SVM的論文的人一定記得什么優(yōu)化的目標(biāo)是要最小化||w||這樣的說法，這是怎么回事呢？回頭再看看我們對間隔和幾何間隔的定義：

間隔：δ=y(wx+b)=|g(x)|

幾何間隔：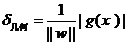

可以看出δ=||w||δ_幾何。注意到幾何間隔與||w||是成反比的，因此最大化幾何間隔與最小化||w||完全是一回事。而我們常用的方法并不是固定||w||的大小而尋求最大幾何間隔，而是固定間隔（例如固定為1），尋找最小的||w||。

而凡是求一個(gè)函數(shù)的最小值（或最大值）的問題都可以稱為尋優(yōu)問題（也叫作一個(gè)規(guī)劃問題），又由于找最大值的問題總可以通過加一個(gè)負(fù)號(hào)變?yōu)檎易钚≈档膯栴}，因此我們下面討論的時(shí)候都針對找最小值的過程來進(jìn)行。一個(gè)尋優(yōu)問題最重要的部分是目標(biāo)函數(shù)，顧名思義，就是指尋優(yōu)的目標(biāo)。例如我們想尋找最小的||w||這件事，就可以用下面的式子表示：

但實(shí)際上對于這個(gè)目標(biāo)，我們常常使用另一個(gè)完全等價(jià)的目標(biāo)函數(shù)來代替，那就是：

(式1)

不難看出當(dāng)||w||²達(dá)到最小時(shí)，||w||也達(dá)到最小，反之亦然（前提當(dāng)然是||w||描述的是向量的長度，因而是非負(fù)的）。之所以采用這種形式，是因?yàn)楹竺娴那蠼膺^程會(huì)對目標(biāo)函數(shù)作一系列變換，而式（1）的形式會(huì)使變換后的形式更為簡潔（正如聰明的讀者所料，添加的系數(shù)二分之一和平方，皆是為求導(dǎo)數(shù)所需）。

接下來我們自然會(huì)問的就是，這個(gè)式子是否就描述了我們的問題呢？（回想一下，我們的問題是有一堆點(diǎn)，可以被分成兩類，我們要找出最好的分類面）

如果直接來解這個(gè)求最小值問題，很容易看出當(dāng)||w||=0的時(shí)候就得到了目標(biāo)函數(shù)的最小值。但是你也會(huì)發(fā)現(xiàn)，無論你給什么樣的數(shù)據(jù)，都是這個(gè)解！反映在圖中，就是H1與H2兩條直線間的距離無限大，這個(gè)時(shí)候，所有的樣本點(diǎn)（無論正樣本還是負(fù)樣本）都跑到了H1和H2中間，而我們原本的意圖是，H1右側(cè)的被分為正類，H2 左側(cè)的被分為負(fù)類，位于兩類中間的樣本則拒絕分類（拒絕分類的另一種理解是分給哪一類都有道理，因而分給哪一類也都沒有道理）。這下可好，所有樣本點(diǎn)都進(jìn)入了無法分類的灰色地帶。

造成這種結(jié)果的原因是在描述問題的時(shí)候只考慮了目標(biāo)，而沒有加入約束條件，約束條件就是在求解過程中必須滿足的條件，體現(xiàn)在我們的問題中就是樣本點(diǎn)必須在H1或H2的某一側(cè)（或者至少在H1和H2上），而不能跑到兩者中間。我們前文提到過把間隔固定為1，這是指把所有樣本點(diǎn)中間隔最小的那一點(diǎn)的間隔定為1（這也是集合的間隔的定義，有點(diǎn)繞嘴），也就意味著集合中的其他點(diǎn)間隔都不會(huì)小于1，按照間隔的定義，滿足這些條件就相當(dāng)于讓下面的式子總是成立：

    y_i[(w·x_i)+b]≥1 (i=1,2,…,l) （l是總的樣本數(shù)）

但我們常常習(xí)慣讓式子的值和0比較，因而經(jīng)常用變換過的形式：

    y_i[(w·x_i)+b]-1≥0 (i=1,2,…,l) （l是總的樣本數(shù)）

因此我們的兩類分類問題也被我們轉(zhuǎn)化成了它的數(shù)學(xué)形式，一個(gè)帶約束的最小值的問題：

下一節(jié)我們從最一般的意義上看看一個(gè)求最小值的問題有何特征，以及如何來解。