現(xiàn)在我們已經(jīng)把一個(gè)本來線性不可分的文本分類問題，通過映射到高維空間而變成了線性可分的。就像下圖這樣：

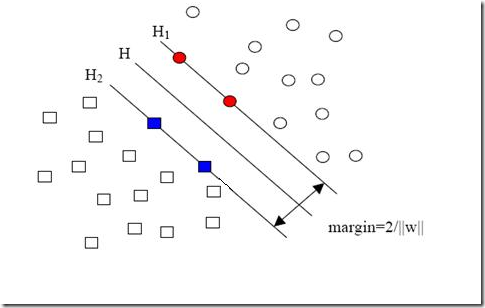
圓形和方形的點(diǎn)各有成千上萬個(gè)（畢竟，這就是我們訓(xùn)練集中文檔的數(shù)量嘛，當(dāng)然很大了）。現(xiàn)在想象我們有另一個(gè)訓(xùn)練集，只比原先這個(gè)訓(xùn)練集多了一篇文章，映射到高維空間以后（當(dāng)然，也使用了相同的核函數(shù)），也就多了一個(gè)樣本點(diǎn)，但是這個(gè)樣本的位置是這樣的：

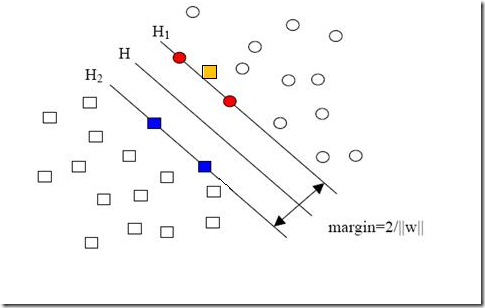
就是圖中黃色那個(gè)點(diǎn)，它是方形的，因而它是負(fù)類的一個(gè)樣本，這單獨(dú)的一個(gè)樣本，使得原本線性可分的問題變成了線性不可分的。這樣類似的問題（僅有少數(shù)點(diǎn)線性不可分）叫做“近似線性可分”的問題。

以我們?nèi)祟惖某ＷR(shí)來判斷，說有一萬個(gè)點(diǎn)都符合某種規(guī)律（因而線性可分），有一個(gè)點(diǎn)不符合，那這一個(gè)點(diǎn)是否就代表了分類規(guī)則中我們沒有考慮到的方面呢（因而規(guī)則應(yīng)該為它而做出修改）？

其實(shí)我們會(huì)覺得，更有可能的是，這個(gè)樣本點(diǎn)壓根就是錯(cuò)誤，是噪聲，是提供訓(xùn)練集的同學(xué)人工分類時(shí)一打瞌睡錯(cuò)放進(jìn)去的。所以我們會(huì)簡(jiǎn)單的忽略這個(gè)樣本點(diǎn)，仍然使用原來的分類器，其效果絲毫不受影響。

但這種對(duì)噪聲的容錯(cuò)性是人的思維帶來的，我們的程序可沒有。由于我們?cè)镜膬?yōu)化問題的表達(dá)式中，確實(shí)要考慮所有的樣本點(diǎn)（不能忽略某一個(gè)，因?yàn)槌绦蛩趺粗涝摵雎阅囊粋€(gè)呢？），在此基礎(chǔ)上尋找正負(fù)類之間的最大幾何間隔，而幾何間隔本身代表的是距離，是非負(fù)的，像上面這種有噪聲的情況會(huì)使得整個(gè)問題無解。這種解法其實(shí)也叫做“硬間隔”分類法，因?yàn)樗残缘囊笏袠颖军c(diǎn)都滿足和分類平面間的距離必須大于某個(gè)值。

因此由上面的例子中也可以看出，硬間隔的分類法其結(jié)果容易受少數(shù)點(diǎn)的控制，這是很危險(xiǎn)的（盡管有句話說真理總是掌握在少數(shù)人手中，但那不過是那一小撮人聊以自慰的詞句罷了，咱還是得民主）。

但解決方法也很明顯，就是仿照人的思路，允許一些點(diǎn)到分類平面的距離不滿足原先的要求。由于不同的訓(xùn)練集各點(diǎn)的間距尺度不太一樣，因此用間隔（而不是幾何間隔）來衡量有利于我們表達(dá)形式的簡(jiǎn)潔。我們?cè)葘?duì)樣本點(diǎn)的要求是：

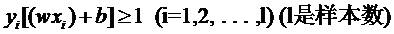
意思是說離分類面最近的樣本點(diǎn)函數(shù)間隔也要比1大。如果要引入容錯(cuò)性，就給1這個(gè)硬性的閾值加一個(gè)松弛變量，即允許

因?yàn)樗沙谧兞渴欠秦?fù)的，因此最終的結(jié)果是要求間隔可以比1小。但是當(dāng)某些點(diǎn)出現(xiàn)這種間隔比1小的情況時(shí)（這些點(diǎn)也叫離群點(diǎn)），意味著我們放棄了對(duì)這些點(diǎn)的精確分類，而這對(duì)我們的分類器來說是種損失。但是放棄這些點(diǎn)也帶來了好處，那就是使分類面不必向這些點(diǎn)的方向移動(dòng)，因而可以得到更大的幾何間隔（在低維空間看來，分類邊界也更平滑）。顯然我們必須權(quán)衡這種損失和好處。好處很明顯，我們得到的分類間隔越大，好處就越多。回顧我們?cè)嫉挠查g隔分類對(duì)應(yīng)的優(yōu)化問題：

||w||²就是我們的目標(biāo)函數(shù)（當(dāng)然系數(shù)可有可無），希望它越小越好，因而損失就必然是一個(gè)能使之變大的量（能使它變小就不叫損失了，我們本來就希望目標(biāo)函數(shù)值越小越好）。那如何來衡量損失，有兩種常用的方式，有人喜歡用

而有人喜歡用

其中l(wèi)都是樣本的數(shù)目。兩種方法沒有大的區(qū)別。如果選擇了第一種，得到的方法的就叫做二階軟間隔分類器，第二種就叫做一階軟間隔分類器。把損失加入到目標(biāo)函數(shù)里的時(shí)候，就需要一個(gè)懲罰因子（cost，也就是libSVM的諸多參數(shù)中的C），原來的優(yōu)化問題就變成了下面這樣：

這個(gè)式子有這么幾點(diǎn)要注意：

一是并非所有的樣本點(diǎn)都有一個(gè)松弛變量與其對(duì)應(yīng)。實(shí)際上只有“離群點(diǎn)”才有，或者也可以這么看，所有沒離群的點(diǎn)松弛變量都等于0（對(duì)負(fù)類來說，離群點(diǎn)就是在前面圖中，跑到H2右側(cè)的那些負(fù)樣本點(diǎn)，對(duì)正類來說，就是跑到H1左側(cè)的那些正樣本點(diǎn)）。

二是松弛變量的值實(shí)際上標(biāo)示出了對(duì)應(yīng)的點(diǎn)到底離群有多遠(yuǎn)，值越大，點(diǎn)就越遠(yuǎn)。

三是懲罰因子C決定了你有多重視離群點(diǎn)帶來的損失，顯然當(dāng)所有離群點(diǎn)的松弛變量的和一定時(shí)，你定的C越大，對(duì)目標(biāo)函數(shù)的損失也越大，此時(shí)就暗示著你非常不愿意放棄這些離群點(diǎn)，最極端的情況是你把C定為無限大，這樣只要稍有一個(gè)點(diǎn)離群，目標(biāo)函數(shù)的值馬上變成無限大，馬上讓問題變成無解，這就退化成了硬間隔問題。

四是懲罰因子C不是一個(gè)變量，整個(gè)優(yōu)化問題在解的時(shí)候，C是一個(gè)你必須事先指定的值，指定這個(gè)值以后，解一下，得到一個(gè)分類器，然后用測(cè)試數(shù)據(jù)看看結(jié)果怎么樣，如果不夠好，換一個(gè)C的值，再解一次優(yōu)化問題，得到另一個(gè)分類器，再看看效果，如此就是一個(gè)參數(shù)尋優(yōu)的過程，但這和優(yōu)化問題本身決不是一回事，優(yōu)化問題在解的過程中，C一直是定值，要記住。

五是盡管加了松弛變量這么一說，但這個(gè)優(yōu)化問題仍然是一個(gè)優(yōu)化問題（汗，這不廢話么），解它的過程比起原始的硬間隔問題來說，沒有任何更加特殊的地方。

從大的方面說優(yōu)化問題解的過程，就是先試著確定一下w，也就是確定了前面圖中的三條直線，這時(shí)看看間隔有多大，又有多少點(diǎn)離群，把目標(biāo)函數(shù)的值算一算，再換一組三條直線（你可以看到，分類的直線位置如果移動(dòng)了，有些原來離群的點(diǎn)會(huì)變得不再離群，而有的本來不離群的點(diǎn)會(huì)變成離群點(diǎn)），再把目標(biāo)函數(shù)的值算一算，如此往復(fù)（迭代），直到最終找到目標(biāo)函數(shù)最小時(shí)的w。

啰嗦了這么多，讀者一定可以馬上自己總結(jié)出來，松弛變量也就是個(gè)解決線性不可分問題的方法罷了，但是回想一下，核函數(shù)的引入不也是為了解決線性不可分的問題么？為什么要為了一個(gè)問題使用兩種方法呢？

其實(shí)兩者還有微妙的不同。一般的過程應(yīng)該是這樣，還以文本分類為例。在原始的低維空間中，樣本相當(dāng)?shù)牟豢煞郑瑹o論你怎么找分類平面，總會(huì)有大量的離群點(diǎn)，此時(shí)用核函數(shù)向高維空間映射一下，雖然結(jié)果仍然是不可分的，但比原始空間里的要更加接近線性可分的狀態(tài)（就是達(dá)到了近似線性可分的狀態(tài)），此時(shí)再用松弛變量處理那些少數(shù)“冥頑不化”的離群點(diǎn)，就簡(jiǎn)單有效得多啦。

本節(jié)中的（式1）也確實(shí)是支持向量機(jī)最最常用的形式。至此一個(gè)比較完整的支持向量機(jī)框架就有了，簡(jiǎn)單說來，支持向量機(jī)就是使用了核函數(shù)的軟間隔線性分類法。

下一節(jié)會(huì)說說松弛變量剩下的一點(diǎn)點(diǎn)東西，順便搞個(gè)讀者調(diào)查，看看大家還想侃侃SVM的哪些方面。