前文提到過，除了開方檢驗（CHI）以外，信息增益（IG，Information Gain）也是很有效的特征選擇方法。但凡是特征選擇，總是在將特征的重要程度量化之后再進行選擇，而如何量化特征的重要性，就成了各種方法間最大的不同。開方檢驗中使用特征與類別間的關聯性來進行這個量化，關聯性越強，特征得分越高，該特征越應該被保留。

在信息增益中，重要性的衡量標準就是看特征能夠為分類系統帶來多少信息，帶來的信息越多，該特征越重要。

因此先回憶一下信息論中有關信息量（就是“熵”）的定義。說有這么一個變量X，它可能的取值有n多種，分別是x1，x2，……，xn，每一種取到的概率分別是P1，P2，……，Pn，那么X的熵就定義為：

clip_image002

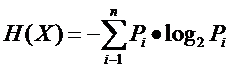
意思就是一個變量可能的變化越多（反而跟變量具體的取值沒有任何關系，只和值的種類多少以及發生概率有關），它攜帶的信息量就越大（因此我一直覺得我們的政策法規信息量非常大，因為它變化很多，基本朝令夕改，笑）。

對分類系統來說，類別C是變量，它可能的取值是C1，C2，……，Cn，而每一個類別出現的概率是P(C1)，P(C2)，……，P(Cn)，因此n就是類別的總數。此時分類系統的熵就可以表示為：

clip_image002[4]

有同學說不好理解呀，這樣想就好了，文本分類系統的作用就是輸出一個表示文本屬于哪個類別的值，而這個值可能是C1，C2，……，Cn，因此這個值所攜帶的信息量就是上式中的這么多。

信息增益是針對一個一個的特征而言的，就是看一個特征t，系統有它和沒它的時候信息量各是多少，兩者的差值就是這個特征給系統帶來的信息量，即增益。系統含有特征t的時候信息量很好計算，就是剛才的式子，它表示的是包含所有特征時系統的信息量。

問題是當系統不包含t時，信息量如何計算？我們換個角度想問題，把系統要做的事情想象成這樣：說教室里有很多座位，學生們每次上課進來的時候可以隨便坐，因而變化是很大的（無數種可能的座次情況）；但是現在有一個座位，看黑板很清楚，聽老師講也很清楚，于是校長的小舅子的姐姐的女兒托關系（真輾轉啊），把這個座位定下來了，每次只能給她坐，別人不行，此時情況怎樣？對于座次的可能情況來說，我們很容易看出以下兩種情況是等價的：（1）教室里沒有這個座位；（2）教室里雖然有這個座位，但其他人不能坐（因為反正它也不能參與到變化中來，它是不變的）。

對應到我們的系統中，就是下面的等價：（1）系統不包含特征t；（2）系統雖然包含特征t，但是t已經固定了，不能變化。

我們計算分類系統不包含特征t的時候，就使用情況（2）來代替，就是計算當一個特征t不能變化時，系統的信息量是多少。這個信息量其實也有專門的名稱，就叫做“條件熵”，條件嘛，自然就是指“t已經固定“這個條件。

但是問題接踵而至，例如一個特征X，它可能的取值有n多種（x1，x2，……，xn），當計算條件熵而需要把它固定的時候，要把它固定在哪一個值上呢？答案是每一種可能都要固定一下，計算n個值，然后取均值才是條件熵。而取均值也不是簡單的加一加然后除以n，而是要用每個值出現的概率來算平均（簡單理解，就是一個值出現的可能性比較大，固定在它上面時算出來的信息量占的比重就要多一些）。

因此有這樣兩個條件熵的表達式：

clip_image002[6]

這是指特征X被固定為值xi時的條件熵，

clip_image002[8]

這是指特征X被固定時的條件熵，注意與上式在意義上的區別。從剛才計算均值的討論可以看出來，第二個式子與第一個式子的關系就是：

clip_image004

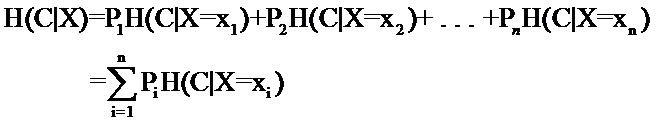
具體到我們文本分類系統中的特征t，t有幾個可能的值呢？注意t是指一個固定的特征，比如他就是指關鍵詞“經濟”或者“體育”，當我們說特征“經濟”可能的取值時，實際上只有兩個，“經濟”要么出現，要么不出現。一般的，t的取值只有t（代表t出現）和clip_image006（代表t不出現），注意系統包含t但t 不出現與系統根本不包含t可是兩回事。

因此固定t時系統的條件熵就有了，為了區別t出現時的符號與特征t本身的符號，我們用T代表特征，而用t代表T出現，那么：

clip_image008

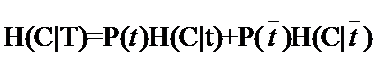
與剛才的式子對照一下，含義很清楚對吧，P(t)就是T出現的概率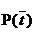，clip_image010就是T不出現的概率。這個式子可以進一步展開，其中的

clip_image012

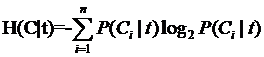
另一半就可以展開為：

clip_image014

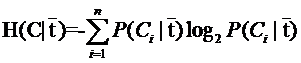
因此特征T給系統帶來的信息增益就可以寫成系統原本的熵與固定特征T后的條件熵之差：

clip_image016

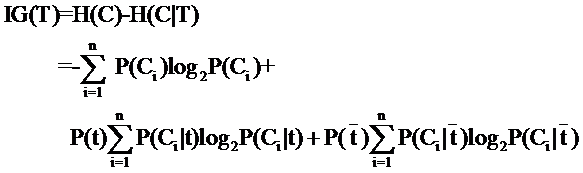
公式中的東西看上去很多，其實也都很好計算。比如P(Ci)，表示類別Ci出現的概率，其實只要用1除以類別總數就得到了（這是說你平等的看待每個類別而忽略它們的大小時這樣算，如果考慮了大小就要把大小的影響加進去）。再比如P(t)，就是特征T出現的概率，只要用出現過T的文檔數除以總文檔數就可以了，再比如P(Ci|t)表示出現T的時候，類別Ci出現的概率，只要用出現了T并且屬于類別Ci的文檔數除以出現了T的文檔數就可以了。

從以上討論中可以看出，信息增益也是考慮了特征出現和不出現兩種情況，與開方檢驗一樣，是比較全面的，因而效果不錯。但信息增益最大的問題還在于它只能考察特征對整個系統的貢獻，而不能具體到某個類別上，這就使得它只適合用來做所謂“全局”的特征選擇（指所有的類都使用相同的特征集合），而無法做“本地”的特征選擇（每個類別有自己的特征集合，因為有的詞，對這個類別很有區分度，對另一個類別則無足輕重）。

看看，導出的過程其實很簡單，沒有什么神秘的對不對。可有的學術論文里就喜歡把這種本來很直白的東西寫得很晦澀，仿佛只有讀者看不懂才是作者的真正成功。

咱們是新一代的學者，咱們沒有知識不怕被別人看出來，咱們有知識也不怕教給別人。所以咱都把事情說簡單點，說明白點，大家好，才是真的好。