按:之前的文章重新匯編一下,修改了一些錯誤和不當(dāng)?shù)恼f法，一起復(fù)習(xí),然后繼續(xù)SVM之旅.

（一）SVM的八股簡介

支持向量機(jī)(Support Vector Machine)是Cortes和Vapnik于1995年首先提出的，它在解決小樣本、非線性及高維模式識別中表現(xiàn)出許多特有的優(yōu)勢，并能夠推廣應(yīng)用到函數(shù)擬合等其他機(jī)器學(xué)習(xí)問題中[10]。
支持向量機(jī)方法是建立在統(tǒng)計(jì)學(xué)習(xí)理論的VC 維理論和結(jié)構(gòu)風(fēng)險(xiǎn)最小原理基礎(chǔ)上的，根據(jù)有限的樣本信息在模型的復(fù)雜性（即對特定訓(xùn)練樣本的學(xué)習(xí)精度，Accuracy）和學(xué)習(xí)能力（即無錯誤地識別任意樣本的能力）之間尋求最佳折衷，以期獲得最好的推廣能力[14]（或稱泛化能力）。

以上是經(jīng)常被有關(guān)SVM 的學(xué)術(shù)文獻(xiàn)引用的介紹，有點(diǎn)八股，我來逐一分解并解釋一下。

Vapnik是統(tǒng)計(jì)機(jī)器學(xué)習(xí)的大牛，這想必都不用說，他出版的《Statistical Learning Theory》是一本完整闡述統(tǒng)計(jì)機(jī)器學(xué)習(xí)思想的名著。在該書中詳細(xì)的論證了統(tǒng)計(jì)機(jī)器學(xué)習(xí)之所以區(qū)別于傳統(tǒng)機(jī)器學(xué)習(xí)的本質(zhì)，就在于統(tǒng)計(jì)機(jī)器學(xué)習(xí)能夠精確的給出學(xué)習(xí)效果，能夠解答需要的樣本數(shù)等等一系列問題。與統(tǒng)計(jì)機(jī)器學(xué)習(xí)的精密思維相比，傳統(tǒng)的機(jī)器學(xué)習(xí)基本上屬于摸著石頭過河，用傳統(tǒng)的機(jī)器學(xué)習(xí)方法構(gòu)造分類系統(tǒng)完全成了一種技巧，一個(gè)人做的結(jié)果可能很好，另一個(gè)人差不多的方法做出來卻很差，缺乏指導(dǎo)和原則。

所謂VC維是對函數(shù)類的一種度量，可以簡單的理解為問題的復(fù)雜程度，VC維越高，一個(gè)問題就越復(fù)雜。正是因?yàn)镾VM關(guān)注的是VC維，后面我們可以看到，SVM解決問題的時(shí)候，和樣本的維數(shù)是無關(guān)的（甚至樣本是上萬維的都可以，這使得SVM很適合用來解決文本分類的問題，當(dāng)然，有這樣的能力也因?yàn)橐肓撕撕瘮?shù)）。

結(jié)構(gòu)風(fēng)險(xiǎn)最小聽上去文縐縐，其實(shí)說的也無非是下面這回事。

機(jī)器學(xué)習(xí)本質(zhì)上就是一種對問題真實(shí)模型的逼近（我們選擇一個(gè)我們認(rèn)為比較好的近似模型，這個(gè)近似模型就叫做一個(gè)假設(shè)），但毫無疑問，真實(shí)模型一定是不知道的（如果知道了，我們干嗎還要機(jī)器學(xué)習(xí)？直接用真實(shí)模型解決問題不就可以了？對吧，哈哈）既然真實(shí)模型不知道，那么我們選擇的假設(shè)與問題真實(shí)解之間究竟有多大差距，我們就沒法得知。比如說我們認(rèn)為宇宙誕生于150億年前的一場大爆炸，這個(gè)假設(shè)能夠描述很多我們觀察到的現(xiàn)象，但它與真實(shí)的宇宙模型之間還相差多少？誰也說不清，因?yàn)槲覀儔焊筒恢勒鎸?shí)的宇宙模型到底是什么。

這個(gè)與問題真實(shí)解之間的誤差，就叫做風(fēng)險(xiǎn)（更嚴(yán)格的說，誤差的累積叫做風(fēng)險(xiǎn)）。我們選擇了一個(gè)假設(shè)之后（更直觀點(diǎn)說，我們得到了一個(gè)分類器以后），真實(shí)誤差無從得知，但我們可以用某些可以掌握的量來逼近它。最直觀的想法就是使用分類器在樣本數(shù)據(jù)上的分類的結(jié)果與真實(shí)結(jié)果（因?yàn)闃颖臼且呀?jīng)標(biāo)注過的數(shù)據(jù)，是準(zhǔn)確的數(shù)據(jù)）之間的差值來表示。這個(gè)差值叫做經(jīng)驗(yàn)風(fēng)險(xiǎn)R_emp(w)。以前的機(jī)器學(xué)習(xí)方法都把經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化作為努力的目標(biāo)，但后來發(fā)現(xiàn)很多分類函數(shù)能夠在樣本集上輕易達(dá)到100%的正確率，在真實(shí)分類時(shí)卻一塌糊涂（即所謂的推廣能力差，或泛化能力差）。此時(shí)的情況便是選擇了一個(gè)足夠復(fù)雜的分類函數(shù)（它的VC維很高），能夠精確的記住每一個(gè)樣本，但對樣本之外的數(shù)據(jù)一律分類錯誤。回頭看看經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化原則我們就會發(fā)現(xiàn)，此原則適用的大前提是經(jīng)驗(yàn)風(fēng)險(xiǎn)要確實(shí)能夠逼近真實(shí)風(fēng)險(xiǎn)才行（行話叫一致），但實(shí)際上能逼近么？答案是不能，因?yàn)闃颖緮?shù)相對于現(xiàn)實(shí)世界要分類的文本數(shù)來說簡直九牛一毛，經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化原則只在這占很小比例的樣本上做到?jīng)]有誤差，當(dāng)然不能保證在更大比例的真實(shí)文本上也沒有誤差。

統(tǒng)計(jì)學(xué)習(xí)因此而引入了泛化誤差界的概念，就是指真實(shí)風(fēng)險(xiǎn)應(yīng)該由兩部分內(nèi)容刻畫，一是經(jīng)驗(yàn)風(fēng)險(xiǎn)，代表了分類器在給定樣本上的誤差；二是置信風(fēng)險(xiǎn)，代表了我們在多大程度上可以信任分類器在未知文本上分類的結(jié)果。很顯然，第二部分是沒有辦法精確計(jì)算的，因此只能給出一個(gè)估計(jì)的區(qū)間，也使得整個(gè)誤差只能計(jì)算上界，而無法計(jì)算準(zhǔn)確的值（所以叫做泛化誤差界，而不叫泛化誤差）。

置信風(fēng)險(xiǎn)與兩個(gè)量有關(guān)，一是樣本數(shù)量，顯然給定的樣本數(shù)量越大，我們的學(xué)習(xí)結(jié)果越有可能正確，此時(shí)置信風(fēng)險(xiǎn)越小；二是分類函數(shù)的VC維，顯然VC維越大，推廣能力越差，置信風(fēng)險(xiǎn)會變大。

泛化誤差界的公式為：

R(w)≤R_emp(w)+Ф(n/h)

公式中R(w)就是真實(shí)風(fēng)險(xiǎn)，R_emp(w)就是經(jīng)驗(yàn)風(fēng)險(xiǎn)，Ф(n/h)就是置信風(fēng)險(xiǎn)。統(tǒng)計(jì)學(xué)習(xí)的目標(biāo)從經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化變?yōu)榱藢で蠼?jīng)驗(yàn)風(fēng)險(xiǎn)與置信風(fēng)險(xiǎn)的和最小，即結(jié)構(gòu)風(fēng)險(xiǎn)最小。

SVM正是這樣一種努力最小化結(jié)構(gòu)風(fēng)險(xiǎn)的算法。

SVM其他的特點(diǎn)就比較容易理解了。

小樣本，并不是說樣本的絕對數(shù)量少（實(shí)際上，對任何算法來說，更多的樣本幾乎總是能帶來更好的效果），而是說與問題的復(fù)雜度比起來，SVM算法要求的樣本數(shù)是相對比較少的。

非線性，是指SVM擅長應(yīng)付樣本數(shù)據(jù)線性不可分的情況，主要通過松弛變量（也有人叫懲罰變量）和核函數(shù)技術(shù)來實(shí)現(xiàn)，這一部分是SVM的精髓，以后會詳細(xì)討論。多說一句，關(guān)于文本分類這個(gè)問題究竟是不是線性可分的，尚沒有定論，因此不能簡單的認(rèn)為它是線性可分的而作簡化處理，在水落石出之前，只好先當(dāng)它是線性不可分的（反正線性可分也不過是線性不可分的一種特例而已，我們向來不怕方法過于通用）。

高維模式識別是指樣本維數(shù)很高，例如文本的向量表示，如果沒有經(jīng)過另一系列文章（《文本分類入門》）中提到過的降維處理，出現(xiàn)幾萬維的情況很正常，其他算法基本就沒有能力應(yīng)付了，SVM卻可以，主要是因?yàn)镾VM 產(chǎn)生的分類器很簡潔，用到的樣本信息很少（僅僅用到那些稱之為“支持向量”的樣本，此為后話），使得即使樣本維數(shù)很高，也不會給存儲和計(jì)算帶來大麻煩（相對照而言，kNN算法在分類時(shí)就要用到所有樣本，樣本數(shù)巨大，每個(gè)樣本維數(shù)再一高，這日子就沒法過了……）。

下一節(jié)開始正式討論SVM。別嫌我說得太詳細(xì)哦。

SVM入門（二）線性分類器Part 1

線性分類器(一定意義上,也可以叫做感知機(jī)) 是最簡單也很有效的分類器形式.在一個(gè)線性分類器中,可以看到SVM形成的思路,并接觸很多SVM的核心概念.

用一個(gè)二維空間里僅有兩類樣本的分類問題來舉個(gè)小例子。如圖所示

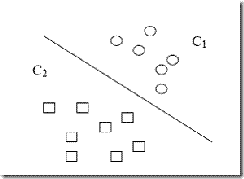
^­C₁和C₂是要區(qū)分的兩個(gè)類別，在二維平面中它們的樣本如上圖所示。中間的直線就是一個(gè)分類函數(shù)，它可以將兩類樣本完全分開。一般的，如果一個(gè)線性函數(shù)能夠?qū)颖就耆_的分開，就稱這些數(shù)據(jù)是線性可分的，否則稱為非線性可分的。

什么叫線性函數(shù)呢？在一維空間里就是一個(gè)點(diǎn)，在二維空間里就是一條直線，三維空間里就是一個(gè)平面，可以如此想象下去，如果不關(guān)注空間的維數(shù)，這種線性函數(shù)還有一個(gè)統(tǒng)一的名稱——超平面（Hyper Plane）！

實(shí)際上，一個(gè)線性函數(shù)是一個(gè)實(shí)值函數(shù)（即函數(shù)的值是連續(xù)的實(shí)數(shù)），而我們的分類問題（例如這里的二元分類問題——回答一個(gè)樣本屬于還是不屬于一個(gè)類別的問題）需要離散的輸出值，例如用1表示某個(gè)樣本屬于類別C₁，而用0表示不屬于（不屬于C₁也就意味著屬于C₂），這時(shí)候只需要簡單的在實(shí)值函數(shù)的基礎(chǔ)上附加一個(gè)閾值即可，通過分類函數(shù)執(zhí)行時(shí)得到的值大于還是小于這個(gè)閾值來確定類別歸屬。 例如我們有一個(gè)線性函數(shù)

g(x)=wx+b

我們可以取閾值為0，這樣當(dāng)有一個(gè)樣本x_i需要判別的時(shí)候，我們就看g(x_i)的值。若g(x_i)>0，就判別為類別C₁，若g(x_i)<0，則判別為類別C₂（等于的時(shí)候我們就拒絕判斷，呵呵）。此時(shí)也等價(jià)于給函數(shù)g(x)附加一個(gè)符號函數(shù)sgn()，即f(x)=sgn [g(x)]是我們真正的判別函數(shù)。

關(guān)于g(x)=wx+b這個(gè)表達(dá)式要注意三點(diǎn)：一，式中的x不是二維坐標(biāo)系中的橫軸，而是樣本的向量表示，例如一個(gè)樣本點(diǎn)的坐標(biāo)是(3,8)，則x^T=(3,8) ，而不是x=3（一般說向量都是說列向量，因此以行向量形式來表示時(shí)，就加上轉(zhuǎn)置）。二，這個(gè)形式并不局限于二維的情況，在n維空間中仍然可以使用這個(gè)表達(dá)式，只是式中的w成為了n維向量（在二維的這個(gè)例子中，w是二維向量，為了表示起來方便簡潔，以下均不區(qū)別列向量和它的轉(zhuǎn)置，聰明的讀者一看便知）；三，g(x)不是中間那條直線的表達(dá)式，中間那條直線的表達(dá)式是g(x)=0，即wx+b=0，我們也把這個(gè)函數(shù)叫做分類面。

實(shí)際上很容易看出來，中間那條分界線并不是唯一的，我們把它稍微旋轉(zhuǎn)一下，只要不把兩類數(shù)據(jù)分錯，仍然可以達(dá)到上面說的效果，稍微平移一下，也可以。此時(shí)就牽涉到一個(gè)問題，對同一個(gè)問題存在多個(gè)分類函數(shù)的時(shí)候，哪一個(gè)函數(shù)更好呢？顯然必須要先找一個(gè)指標(biāo)來量化“好”的程度，通常使用的都是叫做“分類間隔”的指標(biāo)。下一節(jié)我們就仔細(xì)說說分類間隔，也補(bǔ)一補(bǔ)相關(guān)的數(shù)學(xué)知識。

SVM入門（三）線性分類器Part 2

上回說到對于文本分類這樣的不適定問題（有一個(gè)以上解的問題稱為不適定問題），需要有一個(gè)指標(biāo)來衡量解決方案（即我們通過訓(xùn)練建立的分類模型）的好壞，而分類間隔是一個(gè)比較好的指標(biāo)。

在進(jìn)行文本分類的時(shí)候，我們可以讓計(jì)算機(jī)這樣來看待我們提供給它的訓(xùn)練樣本，每一個(gè)樣本由一個(gè)向量（就是那些文本特征所組成的向量）和一個(gè)標(biāo)記（標(biāo)示出這個(gè)樣本屬于哪個(gè)類別）組成。如下：

D_i=(x_i,y_i)

x_i就是文本向量（維數(shù)很高），y_i就是分類標(biāo)記。

在二元的線性分類中，這個(gè)表示分類的標(biāo)記只有兩個(gè)值，1和-1（用來表示屬于還是不屬于這個(gè)類）。有了這種表示法，我們就可以定義一個(gè)樣本點(diǎn)到某個(gè)超平面的間隔：

δ_i=y_i(wx_i+b)

這個(gè)公式乍一看沒什么神秘的，也說不出什么道理，只是個(gè)定義而已，但我們做做變換，就能看出一些有意思的東西。

首先注意到如果某個(gè)樣本屬于該類別的話，那么wx_i+b>0（記得么？這是因?yàn)槲覀兯x的g(x)=wx+b就通過大于0還是小于0來判斷分類），而y_i也大于0；若不屬于該類別的話，那么wx_i+b<0，而y_i也小于0，這意味著y_i(wx_i+b)總是大于0的，而且它的值就等于|wx_i+b|！（也就是|g(x_i)|）

現(xiàn)在把w和b進(jìn)行一下歸一化，即用w/||w||和b/||w||分別代替原來的w和b，那么間隔就可以寫成

這個(gè)公式是不是看上去有點(diǎn)眼熟？沒錯，這不就是解析幾何中點(diǎn)x_i到直線g(x)=0的距離公式嘛！（推廣一下，是到超平面g(x)=0的距離， g(x)=0就是上節(jié)中提到的分類超平面）

小Tips：||w||是什么符號？||w||叫做向量w的范數(shù)，范數(shù)是對向量長度的一種度量。我們常說的向量長度其實(shí)指的是它的2-范數(shù)，范數(shù)最一般的表示形式為p-范數(shù)，可以寫成如下表達(dá)式

    向量w=(w₁, w₂, w₃,…… w_n)

它的p-范數(shù)為

看看把p換成2的時(shí)候，不就是傳統(tǒng)的向量長度么？當(dāng)我們不指明p的時(shí)候，就像||w||這樣使用時(shí)，就意味著我們不關(guān)心p的值，用幾范數(shù)都可以；或者上文已經(jīng)提到了p的值，為了敘述方便不再重復(fù)指明。

當(dāng)用歸一化的w和b代替原值之后的間隔有一個(gè)專門的名稱，叫做幾何間隔，幾何間隔所表示的正是點(diǎn)到超平面的歐氏距離，我們下面就簡稱幾何間隔為“距離”。以上是單個(gè)點(diǎn)到某個(gè)超平面的距離（就是間隔，后面不再區(qū)別這兩個(gè)詞）定義，同樣可以定義一個(gè)點(diǎn)的集合（就是一組樣本）到某個(gè)超平面的距離為此集合中離超平面最近的點(diǎn)的距離。下面這張圖更加直觀的展示出了幾何間隔的現(xiàn)實(shí)含義：

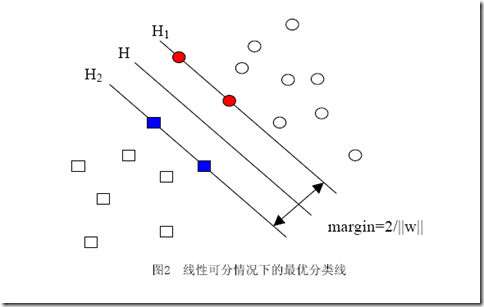
H是分類面，而H₁和H₂是平行于H，且過離H最近的兩類樣本的直線，H₁與H，H₂與H之間的距離就是幾何間隔。

之所以如此關(guān)心幾何間隔這個(gè)東西，是因?yàn)閹缀伍g隔與樣本的誤分次數(shù)間存在關(guān)系：

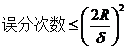
其中的δ是樣本集合到分類面的間隔，R=max ||xi||  i=1,...,n，即R是所有樣本中（xi是以向量表示的第i個(gè)樣本）向量長度最長的值（也就是說代表樣本的分布有多么廣）。先不必追究誤分次數(shù)的具體定義和推導(dǎo)過程，只要記得這個(gè)誤分次數(shù)一定程度上代表分類器的誤差。而從上式可以看出，誤分次數(shù)的上界由幾何間隔決定！（當(dāng)然，是樣本已知的時(shí)候）

至此我們就明白為何要選擇幾何間隔來作為評價(jià)一個(gè)解優(yōu)劣的指標(biāo)了，原來幾何間隔越大的解，它的誤差上界越小。因此最大化幾何間隔成了我們訓(xùn)練階段的目標(biāo)，而且，與二把刀作者所寫的不同，最大化分類間隔并不是SVM的專利，而是早在線性分類時(shí)期就已有的思想。