前文提到過,除了分類算法以外,為分類文本作處理的特征提取算法也對(duì)最終效果有巨大影響,而特征提取算法又分為特征選擇和特征抽取兩大類,其中特征選擇算法有互信息,文檔頻率,信息增益,開方檢驗(yàn)等等十?dāng)?shù)種,這次先介紹特征選擇算法中效果比較好的開方檢驗(yàn)方法。
大家應(yīng)該還記得,開方檢驗(yàn)其實(shí)是數(shù)理統(tǒng)計(jì)中一種常用的檢驗(yàn)兩個(gè)變量獨(dú)立性的方法。(什么?你是文史類專業(yè)的學(xué)生,沒有學(xué)過數(shù)理統(tǒng)計(jì)?那你做什么文本分類?在這搗什么亂?)
開方檢驗(yàn)最基本的思想就是通過觀察實(shí)際值與理論值的偏差來確定理論的正確與否。具體做的時(shí)候常常先假設(shè)兩個(gè)變量確實(shí)是獨(dú)立的(行話就叫做“原假設(shè)”),然后觀察實(shí)際值(也可以叫做觀察值)與理論值(這個(gè)理論值是指“如果兩者確實(shí)獨(dú)立”的情況下應(yīng)該有的值)的偏差程度,如果偏差足夠小,我們就認(rèn)為誤差是很自然的樣本誤差,是測(cè)量手段不夠精確導(dǎo)致或者偶然發(fā)生的,兩者確確實(shí)實(shí)是獨(dú)立的,此時(shí)就接受原假設(shè);如果偏差大到一定程度,使得這樣的誤差不太可能是偶然產(chǎn)生或者測(cè)量不精確所致,我們就認(rèn)為兩者實(shí)際上是相關(guān)的,即否定原假設(shè),而接受備擇假設(shè)。
那么用什么來衡量偏差程度呢?假設(shè)理論值為E(這也是數(shù)學(xué)期望的符號(hào)哦),實(shí)際值為x,如果僅僅使用所有樣本的觀察值與理論值的差值x-E之和
來衡量,單個(gè)的觀察值還好說,當(dāng)有多個(gè)觀察值x1,x2,x3的時(shí)候,很可能x1-E,x2-E,x3-E的值有正有負(fù),因而互相抵消,使得最終的結(jié)果看上好像偏差為0,但實(shí)際上每個(gè)都有偏差,而且都還不小!此時(shí)很直接的想法便是使用方差代替均值,這樣就解決了正負(fù)抵消的問題,即使用
這時(shí)又引來了新的問題,對(duì)于500的均值來說,相差5其實(shí)是很小的(相差1%),而對(duì)20的均值來說,5相當(dāng)于25%的差異,這是使用方差也無法體現(xiàn)的。因此應(yīng)該考慮改進(jìn)上面的式子,讓均值的大小不影響我們對(duì)差異程度的判斷
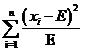 式(1)
式(1)
上面這個(gè)式子已經(jīng)相當(dāng)好了。實(shí)際上這個(gè)式子就是開方檢驗(yàn)使用的差值衡量公式。當(dāng)提供了數(shù)個(gè)樣本的觀察值x1,x2,……xi ,……xn之后,代入到式(1)中就可以求得開方值,用這個(gè)值與事先設(shè)定的閾值比較,如果大于閾值(即偏差很大),就認(rèn)為原假設(shè)不成立,反之則認(rèn)為原假設(shè)成立。
在文本分類問題的特征選擇階段,我們主要關(guān)心一個(gè)詞t(一個(gè)隨機(jī)變量)與一個(gè)類別c(另一個(gè)隨機(jī)變量)之間是否相互獨(dú)立?如果獨(dú)立,就可以說詞t對(duì)類別c完全沒有表征作用,即我們根本無法根據(jù)t出現(xiàn)與否來判斷一篇文檔是否屬于c這個(gè)分類。但與最普通的開方檢驗(yàn)不同,我們不需要設(shè)定閾值,因?yàn)楹茈y說詞t和類別c關(guān)聯(lián)到什么程度才算是有表征作用,我們只想借用這個(gè)方法來選出一些最最相關(guān)的即可。
此時(shí)我們?nèi)匀恍枰靼讓?duì)特征選擇來說原假設(shè)是什么,因?yàn)橛?jì)算出的開方值越大,說明對(duì)原假設(shè)的偏離越大,我們?cè)絻A向于認(rèn)為原假設(shè)的反面情況是正確的。我們能不能把原假設(shè)定為“詞t與類別c相關(guān)“?原則上說當(dāng)然可以,這也是一個(gè)健全的民主主義社會(huì)賦予每個(gè)公民的權(quán)利(笑),但此時(shí)你會(huì)發(fā)現(xiàn)根本不知道此時(shí)的理論值該是多少!你會(huì)把自己繞進(jìn)死胡同。所以我們一般都使用”詞t與類別c不相關(guān)“來做原假設(shè)。選擇的過程也變成了為每個(gè)詞計(jì)算它與類別c的開方值,從大到小排個(gè)序(此時(shí)開方值越大越相關(guān)),取前k個(gè)就可以(k值可以根據(jù)自己的需要選,這也是一個(gè)健全的民主主義社會(huì)賦予每個(gè)公民的權(quán)利)。
好,原理有了,該來個(gè)例子說說到底怎么算了。
比如說現(xiàn)在有N篇文檔,其中有M篇是關(guān)于體育的,我們想考察一個(gè)詞“籃球”與類別“體育”之間的相關(guān)性(任誰(shuí)都看得出來兩者很相關(guān),但很遺憾,我們是智慧生物,計(jì)算機(jī)不是,它一點(diǎn)也看不出來,想讓它認(rèn)識(shí)到這一點(diǎn),只能讓它算算看)。我們有四個(gè)觀察值可以使用:
1.
包含“籃球”且屬于“體育”類別的文檔數(shù),命名為A
2.
包含“籃球”但不屬于“體育”類別的文檔數(shù),命名為B
3.
不包含“籃球”但卻屬于“體育”類別的文檔數(shù),命名為C
4.
既不包含“籃球”也不屬于“體育”類別的文檔數(shù),命名為D
用下面的表格更清晰:
|
特征選擇
|
1.屬于“體育”
|
2.不屬于“體育”
|
總 計(jì)
|
|
1.包含“籃球”
|
A
|
B
|
A+B
|
|
2.不包含“籃球”
|
C
|
D
|
C+D
|
|
總 數(shù)
|
A+C
|
B+D
|
N
|
如果有些特點(diǎn)你沒看出來,那我說一說,首先,A+B+C+D=N(這,這不廢話嘛)。其次,A+C的意思其實(shí)就是說“屬于體育類的文章數(shù)量”,因此,它就等于M,同時(shí),B+D就等于N-M。
好,那么理論值是什么呢?以包含“籃球”且屬于“體育”類別的文檔數(shù)為例。如果原假設(shè)是成立的,即“籃球”和體育類文章沒什么關(guān)聯(lián)性,那么在所有的文章中,“籃球”這個(gè)詞都應(yīng)該是等概率出現(xiàn),而不管文章是不是體育類的。這個(gè)概率具體是多少,我們并不知道,但他應(yīng)該體現(xiàn)在觀察結(jié)果中(就好比拋硬幣的概率是二分之一,可以通過觀察多次拋的結(jié)果來大致確定),因此我們可以說這個(gè)概率接近
(因?yàn)?/span>A+B是包含“籃球”的文章數(shù),除以總文檔數(shù)就是“籃球”出現(xiàn)的概率,當(dāng)然,這里認(rèn)為在一篇文章中出現(xiàn)即可,而不管出現(xiàn)了幾次)而屬于體育類的文章數(shù)為A+C,在這些個(gè)文檔中,應(yīng)該有
篇包含“籃球”這個(gè)詞(數(shù)量乘以概率嘛)。
但實(shí)際有多少呢?考考你(讀者:切,當(dāng)然是A啦,表格里寫著嘛……)。
此時(shí)對(duì)這種情況的差值就得出了(套用式(1)的公式),應(yīng)該是
同樣,我們還可以計(jì)算剩下三種情況的差值D12,D21,D22,聰明的讀者一定能自己算出來(讀者:切,明明是自己懶得寫了……)。有了所有觀察值的差值,就可以計(jì)算“籃球”與“體育”類文章的開方值
把D11,D12,D21,D22的值分別代入并化簡(jiǎn),可以得到
詞t與類別c的開方值更一般的形式可以寫成
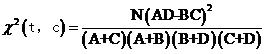 式(2)
式(2)
接下來我們就可以計(jì)算其他詞如“排球”,“產(chǎn)品”,“銀行”等等與體育類別的開方值,然后根據(jù)大小來排序,選擇我們需要的最大的數(shù)個(gè)詞匯作為特征項(xiàng)就可以了。
實(shí)際上式(2)還可以進(jìn)一步化簡(jiǎn),注意如果給定了一個(gè)文檔集合(例如我們的訓(xùn)練集)和一個(gè)類別,則N,M,N-M(即A+C和B+D)對(duì)同一類別文檔中的所有詞來說都是一樣的,而我們只關(guān)心一堆詞對(duì)某個(gè)類別的開方值的大小順序,而并不關(guān)心具體的值,因此把它們從式(2)中去掉是完全可以的,故實(shí)際計(jì)算的時(shí)候我們都使用
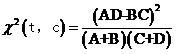 式(3)
式(3)
好啦,并不高深對(duì)不對(duì)?
針對(duì)英文純文本的實(shí)驗(yàn)結(jié)果表明:作為特征選擇方法時(shí),開方檢驗(yàn)和信息增益的效果最佳(相同的分類算法,使用不同的特征選擇算法來得到比較結(jié)果);文檔頻率方法的性能同前兩者大體相當(dāng),術(shù)語(yǔ)強(qiáng)度方法性能一般;互信息方法的性能最差(文獻(xiàn)[17])。
但開方檢驗(yàn)也并非就十全十美了。回頭想想A和B的值是怎么得出來的,它統(tǒng)計(jì)文檔中是否出現(xiàn)詞t,卻不管t在該文檔中出現(xiàn)了幾次,這會(huì)使得他對(duì)低頻詞有所偏袒(因?yàn)樗浯罅说皖l詞的作用)。甚至?xí)霈F(xiàn)有些情況,一個(gè)詞在一類文章的每篇文檔中都只出現(xiàn)了一次,其開方值卻大過了在該類文章99%的文檔中出現(xiàn)了10次的詞,其實(shí)后面的詞才是更具代表性的,但只因?yàn)樗霈F(xiàn)的文檔數(shù)比前面的詞少了“1”,特征選擇的時(shí)候就可能篩掉后面的詞而保留了前者。這就是開方檢驗(yàn)著名的“低頻詞缺陷“。因此開方檢驗(yàn)也經(jīng)常同其他因素如詞頻綜合考慮來?yè)P(yáng)長(zhǎng)避短。
好啦,關(guān)于開方檢驗(yàn)先說這么多,有機(jī)會(huì)還將介紹其他的特征選擇算法。
附:給精通統(tǒng)計(jì)學(xué)的同學(xué)多說幾句,式(1)實(shí)際上是對(duì)連續(xù)型的隨機(jī)變量的差值計(jì)算公式,而我們這里統(tǒng)計(jì)的“文檔數(shù)量“顯然是離散的數(shù)值(全是整數(shù)),因此真正在統(tǒng)計(jì)學(xué)中計(jì)算的時(shí)候,是有修正過程的,但這種修正仍然是只影響具體的開方值,而不影響大小的順序,故文本分類中不做這種修正。