元組關系演算
?
?
???
之前學習了一下關系代數表達式,現在再學習一下元組關系的演算,這樣就全了。這篇東西的符號打出來費了好多時間,比較麻煩,還好看著還能看懂,關鍵是全文本的,好下面開始正文。
???
為了討論方便,先允許關系的基數是無限的。然后再對這種情況下定義的演算作適當的修改,保證關系演算中的每一個公式表示的是有限關系。
???
在元組關系演算系統中,稱
{t|Φ(t)}
為元組演算表達式。其中
t
是元組變量,
Φ(t)
為元組關系演算公式,簡稱公式。
它由原子公式和運算符組成。
?
????
原子公式有三類:
?
??? (1) R(t)
??????? R
是關系名,
t
是元組變量。
R(t)
表示
t
是
R
中的元組。于是,關系
R
可表示為:
{t|R(t)}
??? (2) t[i]
θ
u[j]
??????? t
和
u
是元組變量,
θ
是算術比較運算符。
t[i] θ?u[j]
表示斷言
“
元組
t
的第
i
個分量與元組
u
的第
j
個分量滿足比較關系
θ
”
。例如,
t[2] < u[3]
表示元組
t
的第
2
個分量小于元組
u
的第
3
個分量。
??? (3) t[i]
θ
c
或
?c
θ
t[i]
???????
這里
c
是常量,該公式表示
“t
的第
i
個分量與常量
C
滿足比較關系
θ”
。例如:
t[4]=3
表示元組
t
的第
4
個分量等于
3
。
?
????
在關系演算中定義了
“
自由元組變量
”
和
“
約束元組變量
”
的概念。這些概念和謂詞演算中的概念完全一樣。若公式中的一個元組變量前有
“
全稱量詞
”
或
“
存在量詞
”
,則稱該變量為約束元組變量,否則稱自由元組變量。
?
???
公式可以遞歸定義如下:
?
??? (l)
每個原子公式是公式。
??? (2)
如果
Φ
1
和
Φ
2
是公式,則
Φ
1
∧
Φ
2
、
Φ
1
∨
Φ
2
、
﹁
Φ1
也是公式。分別表示:
???????
①
如果
Φ
1
和
Φ
2
同時為真。則
Φ
1
∧
Φ
2
才為真,否則為假;
???????
②
如果
Φ
1
和
Φ
2
中一個或同時為真,則
Φ
1
∨
Φ
2
為真,僅
Φ
1
和
Φ
2
同時為假時,
Φ
1
∨
Φ
2
才為假;
???????
③
如果
Φ
1
真,則
﹁
Φ
1
為假。
??? (3)
若
Φ
是公式,則
?
t(Φ)
也是公式。其中符號
?
是存在量詞符號,
?
t(Φ)
表示:
???????
若有一個
t
使
Φ
為真,則
?
t(Φ)
為真,否則
?
t(Φ)
為假。
??? (4)
若
Φ
是公式,則
?
t(
Φ
)
也是公式。其中符號
?
是全稱量詞符號,
?
t(
Φ
)
表示:
???????
如果對所有
t
,都使
Φ
為真,則
?
t(
Φ
)
必為真,否則
?
t(
Φ
)
為假。
??? (5)
在元組演算公式中,各種運算符的優先次序為:
???????
①
算術比較運算符最高;
???????
②
量詞次之,且
?
的優先級高于
?
的優先級;
???????
③
邏輯運算符最低,且
﹁
的優先級高于
∧
的優先級,
∧
的優先級高于
∨
的優先級;
???????
④
加括號時,括號中運算符優先,同一括號內的運算符之優先級遵循
①②③
各項。
??? (6)
有限次地使用上述五條規則得到的公式是元組關系演算公式,其他公式不是元組關系演算公式。
?
???
一個元組演算表達式
{t|Φ(t)}
表示了使
Φ(t)
為真的元組集合。
???
關系代數的運算均可以用關系演算表達式來表示
(
反之亦然
)
。下面用關系演算表達式來表示五種基本運算:
?
??? (1)
并
??????? R
∪
S={t|R(t)
∨
S(t)}
??? (2)
差
??????? R
-
S={t|R(t)
∧
﹁
S(t)}
??? (3)
笛卡爾積
??????? R×S={t
(n+m)
|(
?
u
(n)
)(
?
v
(m)
)(R(u)
∧
S(v)
∧
t[1]=u[1]
∧
...
∧
t[n]=u[n]
∧
t[n+1]=v[1]
∧
...
∧
t[n+m]=v[m])}
???????
注:
t
(n+m)
表示
t
有目數
(n+m)
??? (4)
投影
???????
π
t1,t2,...,tk
(R)={t
(k)
|(
?
u
)(R(u)
∧
t[1]=u[i1]
∧
...t[k]=u[ik]
)}
??? (5)
選擇
???????
σ
F
(R)={t|R(t)
∧
F}
???????
注:
F
是公式。
F
用
t[i]
代替
運
算
對
象
i
得到的等價公式。
?
????
例
1
查詢信息系
(IS
系
)
全體學生:
??????? S
IS
={Student(t)
∧
t[5]='IS'}?
????
例
2
查詢年齡小于
20
歲的學生。
????????S
20
={Student(t)
∧
t[4]<20}
????
例
3
查詢學生的姓名和所在系。
????????S={t
(2)
|(
?
u)(Student(u)
∧
t[1]=u[2]
∧
t[2]=u[5])}
???
上面定義的關系演算允許出現無限關系。例如
{t|
﹁
R(t)}
表示所有不屬于
R
的元組
(
元組的目數等于
R
的目數
)
。要求出這些可能的元組是做不到的,所以必須排除這類無意義的表達式。把不產生無限關系的表達式稱為安全表達式,所采取的措施稱為安全限制。安全限制通常是定義一個有限的符號集
dom(Φ)
,
dom(Φ)
一定包括出現在
Φ
以及中間結果和最后結果的關系中的所有符號
(
實際上是各列中值的匯集
)
。
dom(Φ)
不必是最小集。
?
????
當滿足下列條件時,元組演算表達式
{t|Φ(t)}
是安全的:
???
(
1
)如果
t
使
Φ(t)
為真,則
t
的每個分量是
dom(Φ)
中的元素。
???
(
2
)對于
Φ
中每一個形如
(
?
t)(W(u))
的子表達式,若
u
使
W(u)
為真,則
u
的每個分量是
dom(Φ)
中的元素。
???
(
3
)對于
Φ
中每一個形如
(
?
t)(W(u))
的子表達式,若
u
使
W(u)
為假,則
u
的每個分量必屬于
dom(Φ)
。換言之,若
u
某一分量不屬于
dom(Φ)
,則
W(u)
為真。
?
????
例
4
設有關系
R
如圖
2.8(a)
,
S={t|
﹁
R(t)}
,若不進行安全限制,則可能是一個無限關系。所以定義
??????? dom(Φ)=
π
A
(R)
∪
π
B
(R)
∪
π
C
(R)
????????????? ={{a1,a2},{b1,b2},{c1,c2}}
????
則
S
是
dom(Φ)
中各域值中元素的笛卡兒積與
R
的差集。結果如圖
2.8(b)
。注意,在做笛卡兒積時各個域中的元素不能搞混。
?
??? 
?
?
附:其他類型舉例:
-----------------------------------------------------------------------------------------
?
1
、下列等式中恒等的是:
?
①
π
A1,A2
(
σ
F
(E))≡
σ
F
(
π
A1,A2
(E))
②
σ
F
(E
1
×
E
2
)≡
σ
F
(E
1
)
×σ
F
(E
2
)
③
σ
F
(E
1
-E
2
)≡
σ
F
(E
1
)-
σ
F
(E
2
)
④
π
A1,A2,B1,B2
(E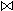 E)≡
π
A1,A2
(E)
E)≡
π
A1,A2
(E)
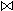 π
B1,B2
(E)
π
B1,B2
(E)
?
①
當
F
包含
A1,A2
以外的限制
時
,不恒等
②
當
F
包含大于
E1(
或
E2)
個數
的限制
時
,不恒等
③
恒等
④
等式不可能成立,右
邊沒
有相同
屬
性
?
2
、以下元
組
的意
義
:
?
{t|(
?
u)((R(u)
∨
S(u))
∧
(
?
v)(T(v)→(
?
w)((R(w)
∨
S(w))
∧
w[1]=u[1]
∧
w[2]=v[1]
∧
w[3]=v[2]))
∧
t[1]=u[1]}
?
據
說
是表示
R
∪
S
÷
T
的意思,但是我
實
在是看不
懂
。
?
3
、以下元
組
表
達
式
轉換為關
系代
數
表
達
式
?
{t|
?
u
?
v(R(u)
∧
S(v)
∧
u[3]=v[1]
∧
u[4]=v[2]
∧
u[1]>v[3]
∧
t[1]=u[2])}
其中
R(A,B,C,D) S(C,D,E)
?
關
系代
數
表
達
式
為
:
π
B
(
σ
A>E
(R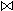 S))
S))
?
4
、把下列
關
系代
數
表
達
式
轉換為
元
組
表
達
式
?
π
1,4
(R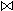 S)
S)
其中
R(A,B,C) S(B,D)
?
元
組
演算表
達
式
為
:
{t|
?
u
?
v(R(u)
∧
S(v)
∧
u[2]=v[1]
∧
t[1]=u[1]
∧
t[2]=v[2])}
?
5
、
關
系代
數
表
達
式
→
元
組
演算表
達
式
?
π
1,5,6
(
σ
1>5
(R×S)) --
注意中
間
是乘法不是自然
連
接
其中
R(A,B,C) S(A,B,C)
?
{t|
?
u
?
v(R(u)
∧
S(v)
∧
u[1]>v[2]
∧
t[1]=u[1]
∧
t[2]=v[2]
∧
t[3]=v[3])}
?
6
、下列
查詢
效率最高的一
組
是:
?
①
E1=
π
A,D
(
σ
B<'2007'
∧
R.C=S.C
∧
E='80'
(R
×
S))
②
E2=
π
A,D
(
σ
R.C=S.C
(
σ
B<'2007'
(R)
×σ
E='80'
(S)))
③
E3=
π
A,D
(
σ
B<'2007'
(R)
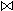 σ
E='80'
(S))
σ
E='80'
(S))
④
E4=
π
A,D
(
σ
B<'2007'
∧
E='80'
(R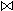 S))
S))
?
答案是
③
,很明
顯
自然
連
接要
優
于笛卡爾
積
,先
運
算再投影
優
于
先投影再
計
算
?
-The End-