前/中/后綴表達式的轉換
?
?
??? 自然表達式轉換為前/中/后綴表達式,其實是很簡單的。首先將自然表達式按照優先級順序,構造出與表達式相對應的二叉樹,然后對二叉樹進行前/中/后綴遍歷,即得到前/中/后綴表達式。
?
??? 舉例說明將自然表達式轉換成二叉樹:
?
??? a×(b+c)-d
?
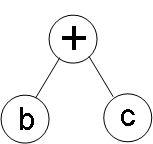
??? ① 根據表達式的優先級順序,首先計算(b+c),形成二叉樹
??? 
???
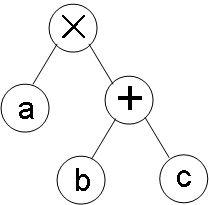
??? ②然后是a×(b+c),在寫時注意左右的位置關系
??? 
?
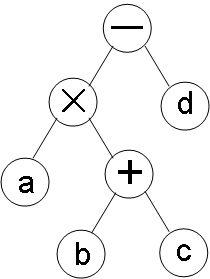
??? ③最后在右邊加上 -d
??? 
?
?
??? 然后最這個構造好的二叉樹進行遍歷,三種遍歷的順序分別是這樣的:
?
??? ① 前序遍歷:根-左-右
??? ② 中序遍歷:左-根-右
??? ③ 后序遍歷:左-右-根
?
??? 所以還是以剛才的這個例子,在最終二叉樹的基礎上可以得出:
?
??? 前綴表達式:-*a+bcd
??? 中綴表達式:a*b+c-d
??? 后綴表達式:abc+*d-
?
?
?
??? 一些其他的遍歷原則:
?
??? 1、深度優先遍歷:
?
??? 首先訪問出發點V,并將其標記為已訪問過;然后依次從V出發搜索V的每個鄰接點W。若W未曾訪問過,則以W為新的出發點繼續進行深度優先遍歷,直至圖中所有和源點V有路徑相通的頂點(亦稱為從源點可達的頂點)均已被訪問為止。若此時圖中仍有未訪問的頂點,則另選一個尚未訪問的頂點作為新的源點重復上述過程,直至圖中所有頂點均被訪問為止。
?
??? 2、廣度優先遍歷:
?
??? 首先訪問出發頂點V,然后訪問與頂點V鄰接的全部未被訪問過的頂點W0,W1,...WK-1;接著再依次訪問與頂點W0,W1,...WK-1鄰接的全部未被訪問過的頂點,以此類推,直至圖的所有頂點都被訪問到,或出發頂點V所在的連通分量的全部頂點都被訪問到為止。
?
??? 注:對于樹來說,深度優先就是從左到右,從上到下;廣度優先就是從上到下,從左到右。
?
-The End-