問題提出:已知數組a[],元素個數為n,現在更改a中的元素,要求得新的a數組中i到j區間內的和(1<=i<=j<=n).
思考:對于這個問題,我們可以暴力地來解決,從a[i]一直累加到a[j],最壞的情況下復雜度為O(n),對于m次change&querry,合起來的復雜度為O(m*n),在n或m很大的情況下,這樣的復雜度是讓人無法忍受的.另外,如果沒有元素的變更,我們完全可以存儲sum[1,k](k=1,2,……),然后對任意給定的查找區間[i,j],都可以方便的用ans=sum[1,j]-sum[1,i-1],當然這只是沒有元素改變的情況下的比較優化的解法.那么對于有元素變更的問題是否有更高效的方法呢?(廢話!沒有我還寫啥?!)可以想一下,每次更改的元素是比較少的,有時候甚至每次只改變一個元素,但是在用暴力方法求區間和的時候,卻對區間內所有的元素都累加了一遍,這樣其實造成了許多無謂的運算.這時候也許會想到如果能把一些結果存起來會不會減少很多運算?答案是肯定的,但問題是怎么存,存什么?如果存任意區間的話,n比較大的時候不但內存吃不消,而且存儲的量太大,不易更改,反而得不償失;那么也許可以考慮存儲特定的一些區間(比如說線段樹,其實現在討論的問題用線段樹完全可以解,以后再詳細寫線段樹).那么現在重新回過頭來,看下這個問題,我們已經確定了要存儲一些特定區間sum的想法,接下來我們要解決的無非是兩個問題:1、減少更改元素后對這些區間里的sum值的更改時間.2、減少查找的時間.
好了廢話了這么半天,無非是想讓自己以及看到的人明白為什么要用樹狀數組.
接下來正式入題.
首先我們可以借鑒元素不變更問題的優化方法,先得到前i-1項之和and前j項之和,以s[i]表示前i項之和,那么sum[i,j]=s[j]-s[i-1].那么現在的問題已經轉化為求前i項之和了.另外,我們已經確定要存儲一些特定區間的和,現在就要來揭示這些特定的區間究竟指什么.
在文字說明之前先引入一個非常經典的,在網上找到的樹狀數組文章里幾乎都要出現的一個圖片
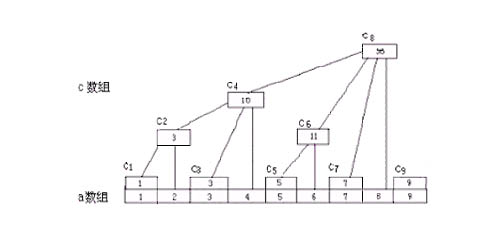
從圖中不難發現,c[k]存儲的實際上是從k開始向前數k的二進制表示中右邊第一個1所代表的數字個元素的和(這么說可能有點拗口,令lowbit為k的二進制表示中右邊第一個1所代表的數字,然后c[k]里存的就是從a[k]開始向前數lowbit個元素之和)這么存有什么好處呢?無論是樹狀數組還是線段樹,都用到了分塊的思想,而樹狀數組采用這樣的存儲結構我想最主要的還是這樣方便計算,我們可以用位運算輕松地算出lowbit.分析一下這樣做的復雜度:對于更改元素來說,如果第i個元素被修改了,因為我們最終還是要求和,所以可以直接在c數組里面進行相應的更改,如圖中的例子,假設更改的元素是a[2],那么它影響到得c數組中的元素只有c[2],c[4],c[8],我們只需一層一層往上修改就可以了,這個過程的最壞的復雜度也不過O(logN);對于查找來說,如查找s[k],只需查找k的二進制表示中1的個數次就能得到最終結果,比如查找s[7],7的二進制表示中有3個1,也就是要查找3次,到底是不是呢,我們來看上圖,s[7]=c[7]+c[6]+c[4],可能你還不知道怎么實現這個過程.
還以7為例,二進制為0111,右邊第一個1出現在第0位上,也就是說要從a[7]開始向前數1個元素(只有a[7]),即c[7];
然后將這個1舍掉,得到6,二進制表示為0110,右邊第一個1出現在第1位上,也就是說要從a[6]開始向前數2個元素(a[6],a[5]),即c[6];
然后舍掉用過的1,得到4,二進制表示為0100,右邊第一個1出現在第2位上,也就是說要從a[4]開始向前數4個元素(a[4],a[3],a[2],a[1]),即c[4].
代碼實現:

 Code
Code
 int lowbit(int x)//計算lowbit
int lowbit(int x)//計算lowbit


 {
{
 return x&(-x);
return x&(-x);
 }
}
 void add(int i,int val)//將第i個元素更改為val
void add(int i,int val)//將第i個元素更改為val


 {
{
 while(i<=n)
while(i<=n)


 {
{
 c[i]+=val;
c[i]+=val;
 i+=lowbit(i);
i+=lowbit(i);
 }
}
 }
}
 int sum(int i)//求前i項和
int sum(int i)//求前i項和


 {
{
 int s=0;
int s=0;
 while(i>0)
while(i>0)


 {
{
 s+=c[i];
s+=c[i];
 i-=lowbit(i);
i-=lowbit(i);
 }
}
 return s;
return s;
 }
}
http://www.cnblogs.com/yykkciwei/archive/2009/05/08/1452889.htmlposted on 2010-05-08 20:22
何克勤 閱讀(293)
評論(0) 編輯 收藏 所屬分類:
Algorithm and Data Structure