Posted on 2010-04-01 22:22
Norvid 閱讀(71695)
評論(9) 編輯 收藏 所屬分類:
讀書筆記

最近在擺弄數據離散度的時候遇到一種圖形,叫做盒圖(boxplot)。它對于顯示數據的離散的分布情況效果不錯。
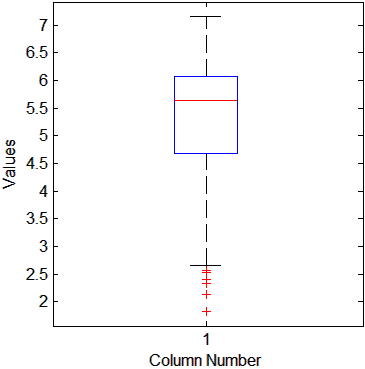
盒圖是在1977年由美國的統計學家約翰·圖基(John Tukey)發明的。它由五個數值點組成:最小值(min),下四分位數(Q1),中位數(median),上四分位數(Q3),最大值(max)。也可以往盒圖里面加入平均值(mean)。如上圖。下四分位數、中位數、上四分位數組成一個“帶有隔間的盒子”。上四分位數到最大值之間建立一條延伸線,這個延伸線成為“胡須(whisker)”。
由于現實數據中總是存在各式各樣地“臟數據”,也成為“離群點”,于是為了不因這些少數的離群數據導致整體特征的偏移,將這些離群點單獨匯出,而盒圖中的胡須的兩級修改成最小觀測值與最大觀測值。這里有個經驗,就是最大(最小)觀測值設置為與四分位數值間距離為1.5個IQR(中間四分位數極差)。即
- IQR = Q3-Q1,即上四分位數與下四分位數之間的差,也就是盒子的長度。
- 最小觀測值為min = Q1 - 1.5*IQR,如果存在離群點小于最小觀測值,則胡須下限為最小觀測值,離群點單獨以點匯出。如果沒有比最小觀測值小的數,則胡須下限為最小值。
- 最大觀測值為max = Q3 -1.5*IQR,如果存在離群點大于最大觀測值,則胡須上限為最大觀測值,離群點單獨以點匯出。如果沒有比最大觀測值大的數,則胡須上限為最大值。
通過盒圖,在分析數據的時候,盒圖能夠有效地幫助我們識別數據的特征:
- 直觀地識別數據集中的異常值(查看離群點)。
- 判斷數據集的數據離散程度和偏向(觀察盒子的長度,上下隔間的形狀,以及胡須的長度)。