update:更正選擇中數的描述,在7到39之間的數組大小選擇median-of-three來選擇pivot,大小等于7的數組則直接使用中數作為pivot。
quicksort可以說是應用最廣泛的排序算法之一,它的基本思想是分治法,選擇一個pivot(中軸點),將小于pivot放在左邊,將大于pivot放在右邊,針對左右兩個子序列重復此過程,直到序列為空或者只有一個元素。這篇blog主要目的是關注quicksort可能的改進方法,并對這些改進方法做評測。其目的是為了理解Arrays.sort(int [ ]a)的實現。實現本身有paper介紹。
quicksort一個教科書式的簡單實現,采用左端點做pivot(《算法導論》上偽代碼是以右端點做pivot):
public void qsort1(int[] a, int p, int r) {
// 0個或1個元素,返回
if (p >= r)
return;
// 選擇左端點為pivot
int x = a[p];
int j = p;
for (int i = p + 1; i <= r; i++) {
// 小于pivot的放到左邊
if (a[i] < x) {
swap(a, ++j, i);
}
}
// 交換左端點和pivot位置
swap(a, p, j);
// 遞歸子序列
qsort1(a, p, j - 1);
qsort1(a, j + 1, r);
}
其中的swap用于交換數組元素:
public static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
quicksort的最佳情況下的時間復雜度O(n logn),最壞情況下的時間復雜度是O(n^2),退化到插入排序的最壞情況,平均情況下的平均復雜度接近于最佳情況也就是O(nlog n),這也是基于比較的排序算法的比較次數下限。
為了對排序算法的性能改進有個直觀的對比,我們建立一個測試基準,分別測試隨機數組的排序、升序數組的排序、降序數組的排序以及重復元素的數組排序。首先使用java.util.Arrays.sort建立一個評測基準,注意這里的時間單位是秒,這些絕對時間沒有意義,我們關注的是相對值,因此這里我不會列出詳細的評測程序:
| 算法 |
隨機數組 |
升序數組 |
降序數組 |
重復數組 |
| Arrays.sort |
136.293 |
0.548 |
0.524 |
26.822 |
qsort1對于輸入做了假設,假設輸入是隨機的數組,如果排序已經排序的數組,qsort1馬上退化到O(n^2)的復雜度,這是由于選定的pivot每次都會跟剩余的所有元素做比較。它跟Arrays.sort的比較:
| 算法 |
隨機數組 |
升序數組 |
降序數組 |
重復數組 |
| Arrays.sort |
136.293 |
0.548 |
0.524 |
26.822 |
| qsort1 |
134.475 |
48.498 |
141.968 |
45.244 |
果然,在排序已經排序的數組的時候,qsort的性能跟Arrays.sort的差距太大了。那么我們能做的第一個優化是什么?答案是將pivot的選擇隨機化,不再是固定選擇左端點,而是利用隨機數產生器選擇一個有效的位置作為pivot,這就是qsort2:
public void qsort2(int[] a, int p, int r) {
// 0個或1個元素,返回
if (p >= r)
return;
// 隨機選擇pivot
int i = p + rand.nextInt(r - p + 1);
// 交換pivot和左端點
swap(a, p, i);
// 劃分算法不變
int x = a[p];
int j = p;
for (i = p + 1; i <= r; i++) {
// 小于pivot的放到左邊
if (a[i] < x) {
swap(a, ++j, i);
}
}
// 交換左端點和pivot位置
swap(a, p, j);
// 遞歸子序列
qsort2(a, p, j - 1);
qsort2(a, j + 1, r);
}
再次進行測試,查看qsort1和qsort2的對比:
| 算法 |
隨機數組 |
升序數組 |
降序數組 |
重復數組 |
| qsort1 |
134.475 |
48.498 |
141.968 |
45.244 |
| qsort2 |
227.87 |
19.009 |
18.597 |
74.639 |
從隨機數組的排序來看,qsort2比之qsort1還有所下降,這主要是隨機數產生器帶來的消耗,但是在已經排序數組的排序上面,qsort2有很大進步,在有大量隨機重復元素的數組排序上,qsort2卻有所下降,主要消耗也是來自隨機數產生器的影響。
更進一步的優化是在劃分算法上,現在的劃分算法只使用了一個索引i,i從左向右掃描,遇到比pivot小的,就跟從p+1開始的位置(由j索引進行遞增標志)進行交換,最終的劃分點落在了j,然后將pivot調換到j上,再遞歸排序左右兩邊子序列。一個更高效的劃分過程是使用兩個索引i和j,分別從左右兩端進行掃描,i掃描到大于等于pivot的元素就停止,j掃描到小于等于pivot的元素也停止,交換兩個元素,持續這個過程直到兩個索引相遇,此時的pivot的位置就落在了j,然后交換pivot和j的位置,后續的工作沒有不同,示意圖

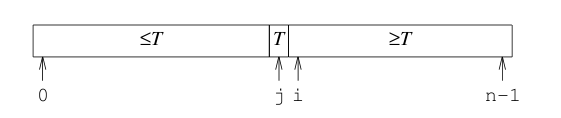
改進后的qsort3代碼如下:
public void qsort3(int[] a, int p, int r) {
if (p >= r)
return;
// 隨機選
int i = p + rand.nextInt(r - p + 1);
swap(a, p, i);
// 左索引i指向左端點
i = p;
// 右索引j初始指向右端點
int j = r + 1;
int x = a[p];
while (true) {
// 查找比x大于等于的位置
do {
i++;
} while (i <= r && a[i] < x);
// 查找比x小于等于的位置
do {
j--;
} while (a[j] > x);
if (j < i)
break;
// 交換a[i]和a[j]
swap(a, i, j);
}
swap(a, p, j);
qsort3(a, p, j - 1);
qsort3(a, j + 1, r);
}
這里要用do……while是因為i索引的初始位置是pivot值存儲的左端點,而j所在初始位置是右端點之外,因此都需要先移動一個位置才是合法的。查看下qsort2和qsort3的基準測試對比:
| 算法 |
隨機數組 |
升序數組 |
降序數組 |
重復數組 |
| qsort2 |
227.87 |
19.009 |
18.597 |
74.639 |
| qsort3 |
229.44 |
18.696 |
18.507 |
43.428 |
可以看到qsort3的改進主要體現在了大量重復元素的數組的排序上,這是因為qsort3在遇到跟pivot相等的元素的時候,還是進行停止并交換,而非跳過;假設遇到相等的元素你不停止,那么這些相等的元素在下次劃分的時候需要再次進行比較,比較次數退化到最差情況的O(n^2),而通過在遇到相等元素的時候停止并交換,盡管增加了交換的次數,但是卻避免了所有元素相同情況下最差情況的發生。
改進到這里,回頭看看我們做了什么,首先是使用隨機挑選pivot替代固定選擇,其次是改進了劃分算法,從兩端進行掃描替代單向查找,并仔細處理元素相同的情況。
插入排序的時間復雜度是O(N^2),但是在已經排序好的數組上面,插入排序的最佳情況是O(n),插入排序在小數組的排序上是非常高效的,這給我們一個提示,在快速排序遞歸的子序列,如果序列規模足夠小,可以使用插入排序替代快速排序,因此可以在快排之前判斷數組大小,如果小于一個閥值就使用插入排序,這就是qsort4:
public void qsort4(int[] a, int p, int r) {
if (p >= r)
return;
// 在數組大小小于7的情況下使用快速排序
if (r - p + 1 < 7) {
for (int i = p; i <= r; i++) {
for (int j = i; j > p && a[j - 1] > a[j]; j--) {
swap(a, j, j - 1);
}
}
return;
}
int i = p + rand.nextInt(r - p + 1);
swap(a, p, i);
i = p;
int j = r + 1;
int x = a[p];
while (true) {
do {
i++;
} while (i <= r && a[i] < x);
do {
j--;
} while (a[j] > x);
if (j < i)
break;
swap(a, i, j);
}
swap(a, p, j);
qsort4(a, p, j - 1);
qsort4(a, j + 1, r);
}
如果數組大小小于7就使用插入排序,7這個數字完全是經驗值。查看qsort3和qsort4的測試比較:
| 算法 |
隨機數組 |
升序數組 |
降序數組 |
重復數組 |
| qsort3 |
229.44 |
18.696 |
18.507 |
43.428 |
| qsort4 |
173.201 |
7.436 |
7.477 |
32.195 |
qsort4改進的效果非常明顯,所有基準測試的結果都取得了明顯的進步。qsort4還有一種變形,現在是在每個遞歸的子序列上進行插入排序,也可以換一種形式,當小于某個特定閥值的時候直接返回不進行任何排序,在遞歸返回之后,
對整個數組進行一次插入排序,這個時候整個數組是由一個一個沒有排序的子序列按照順序組成的,因此插入排序可以很快地將整個數組排序,這個變形的qsort5跟qsort4沒有本質上的不同:
public void qsort5(int[] a, int p, int r) {
if (p >= r)
return;
// 遞歸子序列,并且數組大小小于7,直接返回
if (p != 0 && r!=(a.length-1) && r - p + 1 < 7)
return;
// 隨機選
int i = p + rand.nextInt(r - p + 1);
swap(a, p, i);
i = p;
int j = r + 1;
int x = a[p];
while (true) {
do {
i++;
} while (i <= r && a[i] < x);
do {
j--;
} while (a[j] > x);
if (j < i)
break;
swap(a, i, j);
}
swap(a, p, j);
qsort5(a, p, j - 1);
qsort5(a, j + 1, r);
// 最后對整個數組進行插入排序
if (p == 0 && r==a.length-1) {
for (i = 0; i <= r; i++) {
for (j = i; j > 0 && a[j - 1] > a[j]; j--) {
swap(a, j, j - 1);
}
}
return;
}
}
基準測試的結果也證明了qsort4和qsort5是一樣的:
| 算法 |
隨機數組 |
升序數組 |
降序數組 |
重復數組 |
| qsort4 |
173.201 |
7.436 |
7.477 |
32.195 |
| qsort5 |
175.031 |
7.324 |
7.453 |
32.322 |
現在,最大的開銷還是隨機數產生器選擇pivot帶來的開銷,我們用隨機數產生器來選擇pivot,是希望pivot能盡量將數組劃分得均勻一些,可以選擇一個替代方案來替代隨機數產生器來選擇pivot,比如三數取中,通過對序列的first、middle和last做比較,選擇三個數的中間大小的那一個做pivot,從概率上可以將比較次數下降到12/7 ln(n)。
median-of-three對小數組來說有很大的概率選擇到一個比較好的pivot,但是對于大數組來說就不足以保證能夠選擇出一個好的pivot,因此還有個辦法是所謂median-of-nine,這個怎么做呢?它是先從數組中分三次取樣,每次取三個數,三個樣品各取出中數,然后從這三個中數當中再取出一個中數作為pivot,也就是median-of-medians。取樣也不是亂來,分別是在左端點、中點和右端點取樣。什么時候采用median-of-nine去選擇pivot,這里也有個數組大小的閥值,這個值也完全是經驗值,設定在40,
大小大于40的數組使用median-of-nine選擇pivot,大小在7到40之間的數組使用median-of-three選擇中數,大小等于7的數組直接選擇中數,大小小于7的數組則直接使用插入排序,這就是改進后的qsort6,已經非常接近于Arrays.sort的實現:
public void qsort6(int[] a, int p, int r) {
if (p >= r)
return;
// 在數組大小小于7的情況下使用快速排序
if (r - p + 1 < 7) {
for (int i = p; i <= r; i++) {
for (int j = i; j > p && a[j - 1] > a[j]; j--) {
swap(a, j, j - 1);
}
}
return;
}
// 計算數組長度
int len = r - p + 1;
// 求出中點,大小等于7的數組直接選擇中數
int m = p + (len >> 1);
// 大小大于7
if (len > 7) {
int l = p;
int n = p + len - 1;
if (len > 40) { // 大數組,采用median-of-nine選擇
int s = len / 8;
l = med3(a, l, l + s, l + 2 * s); // 取樣左端點3個數并得出中數
m = med3(a, m - s, m, m + s); // 取樣中點3個數并得出中數
n = med3(a, n - 2 * s, n - s, n); // 取樣右端點3個數并得出中數
}
m = med3(a, l, m, n); // 取中數中的中數,median-of-three
}
// 交換pivot到左端點,后面的操作與qsort4相同
swap(a, p, m);
m = p;
int j = r + 1;
int x = a[p];
while (true) {
do {
m++;
} while (m <= r && a[m] < x);
do {
j--;
} while (a[j] > x);
if (j < m)
break;
swap(a, m, j);
}
swap(a, p, j);
qsort6(a, p, j - 1);
qsort6(a, j + 1, r);
}
其中的med3函數用于取三個數的中數:
private static int med3(int x[], int a, int b, int c) {
return x[a] < x[b] ? (x[b] < x[c] ? b : x[a] < x[c] ? c : a)
: x[b] > x[c] ? b : x[a] > x[c] ? c : a;
}
運行基準測試跟qsort4進行比較:
| 算法 |
隨機數組 |
升序數組 |
降序數組 |
重復數組 |
| qsort4 |
173.201 |
7.436 |
7.477 |
32.195 |
| qsort6 |
143.264 |
0.54 |
0.836 |
27.311 |
觀察到qsort6的改進也非常明顯,消除了隨機產生器帶來的開銷,取中數的時間復雜度在O(1)。此時qsort6跟Arrays.sort的差距已經非常小了。Array.sort所做的最后一個改進是針對劃分算法,采用了所謂"split-end"的劃分算法,這主要是為了針對equals的元素,降低equals元素參與遞歸的開銷。我們原來的劃分算法是分為兩個區域加上一個pivot:

跟pivot equals的元素分散在左右兩個子序列里,繼續參與遞歸調用。當數組里的相同元素很多的時候,這個開銷是不可忽視的,因此一個方案是將這些相同的元素集中存放到中間這個地方,不參與后續的遞歸處理,這就是"fat partition",此時是將數組劃分為3個區域:小于pivot,等于pivot以及大于pivot:

但是Arrays.sort采用的卻不是"fat partition",這是因為fat partition的實現比較復雜并且低效,Arrays.sort是將與pivot相同的元素劃分到兩端,也就是將數組分為了4個區域:
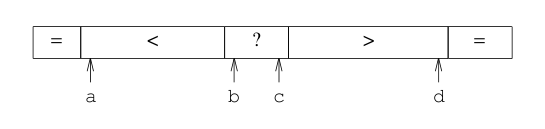

這就是split-end名稱的由來,這個算法的實現可以跟qsort3的改進結合起來,同樣是進行兩端掃描,但是遇到equals的元素不是進行互換,而是各自交換到兩端。當掃描結束,還要將兩端這些跟pivot equals的元素交換到中間位置,不相同的元素交換到兩端,左邊仍然是比pivot小的,右邊是比pivot大的,分別進行遞歸的快速排序處理,這樣改進后的算法我們成為qsort7:
public void qsort7(int[] x, int p, int r) {
if (p >= r)
return;
// 在數組大小小于7的情況下使用快速排序
if (r - p + 1 < 7) {
for (int i = p; i <= r; i++) {
for (int j = i; j > p && x[j - 1] > x[j]; j--) {
swap(x, j, j - 1);
}
}
return;
}
// 選擇中數,與qsort6相同。
int len = r - p + 1;
int m = p + (len >> 1);
if (len > 7) {
int l = p;
int n = p + len - 1;
if (len > 40) {
int s = len / 8;
l = med3(x, l, l + s, l + 2 * s);
m = med3(x, m - s, m, m + s);
n = med3(x, n - 2 * s, n - s, n);
}
m = med3(x, l, m, n);
}
int v = x[m];
// a,b進行左端掃描,c,d進行右端掃描
int a = p, b = a, c = p + len - 1, d = c;
while (true) {
// 嘗試找到大于pivot的元素
while (b <= c && x[b] <= v) {
// 與pivot相同的交換到左端
if (x[b] == v)
swap(x, a++, b);
b++;
}
// 嘗試找到小于pivot的元素
while (c >= b && x[c] >= v) {
// 與pivot相同的交換到右端
if (x[c] == v)
swap(x, c, d--);
c--;
}
if (b > c)
break;
// 交換找到的元素
swap(x, b++, c--);
}
// 將相同的元素交換到中間
int s, n = p + len;
s = Math.min(a - p, b - a);
vecswap(x, p, b - s, s);
s = Math.min(d - c, n - d - 1);
vecswap(x, b, n - s, s);
// 遞歸調用子序列
if ((s = b - a) > 1)
qsort7(x, p, s + p - 1);
if ((s = d - c) > 1)
qsort7(x, n - s, n - 1);
}
其中用到了vecswap方法用于批量交換一批數據,將a位置(包括a)之后n個元素與b位置(包括b)之后n個元素進行交換:
private static void vecswap(int x[], int a, int b, int n) {
for (int i = 0; i < n; i++, a++, b++)
swap(x, a, b);
}
主要是用于劃分后將兩端與pivot相同的元素交換到中間來。qsort7的實現跟Arrays.sort的實現是一樣的,看看split-end劃分帶來的改進跟qsort6的對比:
| 算法 |
隨機數組 |
升序數組 |
降序數組 |
重復數組 |
| qsort6 |
143.264 |
0.54 |
0.836 |
27.311 |
| qsort6 |
140.468 |
0.491 |
0.506 |
26.639 |
這個結果跟Arrays.sort保持一致。
最后給幾張7個快排程序的在4種測試中的對比圖




還可以做的優化:
1、內聯swap和vecswap函數,循環中的swap調用可以展開。
2、改進插入排序,這是《編程珠璣》里提到的,減少取值次數。
for (int i = p; i <= r; i++) {
int t = x[i];
int j = i;
for (; j > p && x[j - 1] > t; j--) {
x[j] = x[j - 1];
}
x[j] = t;
}
3、遞歸可以展開為循環,最后一個遞歸調用是尾遞歸調用,很容易展開為循環,左子序列的遞歸調用就沒那么容易展開了。
4、嘗試更多取樣算法來提高選擇好的pivot的概率。
5、并行處理子序列