判定一個點是否在三角形內
如何判定一個點P是否存在于指定的三角形ABC內,這肯定是一個簡單的問題,本文僅用一個圖形界面程序展示了該問題,有興趣的朋友可以看看。(2008.07.24最后更新)
在此處使用一種常見且簡便的方法:如果三角形PAB,PAC和PBC的面積之和與三角形ABC的面積相等,即可判定點P在三角形ABC內(包括在三條邊上)。
可知,該方法的關鍵在于如何計算三角形的面積。幸運地是,當知道三角形頂點(A,B和C)的坐標((Ax, Ay),(Bx, By)和(Cx, Cy))之后,即可計算出其面積:
S = |(Ax * By + Bx * Cy + Cx * Zy - Ay * Bx - By * Cx - Cy * Ax) / 2|
關鍵的代碼如下,
// 由給定的三個頂點的坐標,計算三角形面積。
// Point(java.awt.Point)代表點的坐標。
private static double triangleArea(Point pos1, Point pos2, Point pos3) {
double result = Math.abs((pos1.x * pos2.y + pos2.x * pos3.y + pos3.x * pos1.y
- pos2.x * pos1.y - pos3.x * pos2.y - pos1.x * pos3.y) / 2.0D);
return result;
}
// 判斷點pos是否在指定的三角形內。
private static boolean inTriangle(Point pos, Point posA, Point posB,
Point posC) {
double triangleArea = triangleArea(posA, posB, posC);
double area = triangleArea(pos, posA, posB);
area += triangleArea(pos, posA, posC);
area += triangleArea(pos, posB, posC);
double epsilon = 0.0001; // 由于浮點數的計算存在著誤差,故指定一個足夠小的數,用于判定兩個面積是否(近似)相等。
if (Math.abs(triangleArea - area) < epsilon) {
return true;
}
return false;
}
執行該應用程序,用鼠標在其中點擊三次,即可繪制一個三角形,如下組圖所示:
然后僅需移動鼠標,就會出現一個空心圓圈。如果圓圈的中心在三角內(包含在三條邊上),則圓圈顯示為紅色;否則,顯示為藍色。如下組圖所示:
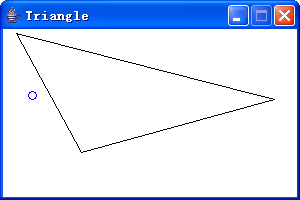
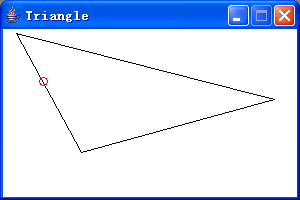
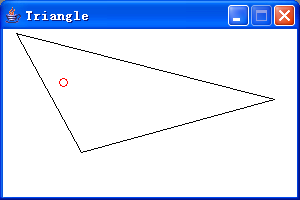
完整代碼如下:
public class CanvasPanel extends JPanel {
private static final long serialVersionUID = -6665936180725885346L;
private Point firstPoint = null;
private Point secondPoint = null;
private Point thirdPoint = null;
public CanvasPanel() {
setBackground(Color.WHITE);
addMouseListener(mouseAdapter);
addMouseMotionListener(mouseAdapter);
}
public void paintComponent(Graphics g) {
super.paintComponent(g);
drawTriangel(g);
}
private void drawTriangel(Graphics g) {
if (firstPoint != null && secondPoint != null) {
g.drawLine(firstPoint.x, firstPoint.y, secondPoint.x, secondPoint.y);
if (thirdPoint != null) {
g.drawLine(firstPoint.x, firstPoint.y, thirdPoint.x, thirdPoint.y);
g.drawLine(secondPoint.x, secondPoint.y, thirdPoint.x, thirdPoint.y);
}
}
}
private static boolean inTriangle(Point pos, Point posA, Point posB,
Point posC) {
double triangeArea = triangleArea(posA, posB, posC);
double area = triangleArea(pos, posA, posB);
area += triangleArea(pos, posA, posC);
area += triangleArea(pos, posB, posC);
double epsilon = 0.0001;
if (Math.abs(triangeArea - area) < epsilon) {
return true;
}
return false;
}
private static double triangleArea(Point pos1, Point pos2, Point pos3) {
double result = Math.abs((pos1.x * pos2.y + pos2.x * pos3.y + pos3.x * pos1.y
- pos2.x * pos1.y - pos3.x * pos2.y - pos1.x * pos3.y) / 2.0D);
return result;
}
private MouseInputAdapter mouseAdapter = new MouseInputAdapter() {
public void mouseReleased(MouseEvent e) {
Point pos = e.getPoint();
if (firstPoint == null) {
firstPoint = pos;
} else if (secondPoint == null) {
secondPoint = pos;
Graphics g = CanvasPanel.this.getGraphics();
CanvasPanel.this.paintComponent(g);
g.drawLine(firstPoint.x, firstPoint.y, secondPoint.x, secondPoint.y);
} else if (thirdPoint == null) {
thirdPoint = pos;
Graphics g = CanvasPanel.this.getGraphics();
CanvasPanel.this.paintComponent(g);
g.drawLine(firstPoint.x, firstPoint.y, secondPoint.x, secondPoint.y);
g.drawLine(firstPoint.x, firstPoint.y, thirdPoint.x, thirdPoint.y);
g.drawLine(secondPoint.x, secondPoint.y, thirdPoint.x, thirdPoint.y);
}
}
public void mouseMoved(MouseEvent e) {
Point pos = e.getPoint();
Graphics2D g2 = (Graphics2D) CanvasPanel.this.getGraphics();
CanvasPanel.this.paintComponent(g2);
if (firstPoint != null && secondPoint == null) {
g2.drawLine(firstPoint.x, firstPoint.y, pos.x, pos.y);
} else if (firstPoint != null && secondPoint != null && thirdPoint == null) {
g2.drawLine(firstPoint.x, firstPoint.y, pos.x, pos.y);
g2.drawLine(secondPoint.x, secondPoint.y, pos.x, pos.y);
} else if (firstPoint != null && secondPoint != null && thirdPoint != null) {
if (inTriangle(pos, firstPoint, secondPoint, thirdPoint)) {
g2.setColor(Color.RED);
} else {
g2.setColor(Color.BLUE);
}
int radius = 4;
g2.drawOval(pos.x - radius, pos.y - radius, radius * 2, radius * 2);
}
}
};
}
public class Triangle extends JFrame {
private static final long serialVersionUID = 1L;
private CanvasPanel mainPanel = null;
public Triangle() {
setTitle("Triangle");
setSize(new Dimension(300, 200));
setResizable(false);
init();
Container container = getContentPane();
container.add(mainPanel);
setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
setVisible(true);
}
private void init() {
mainPanel = new CanvasPanel();
}
public static void main(String[] args) {
new Triangle();
}
}