http://wiki.mbalib.com/wiki/%E6%96%B9%E5%B7%AE
方差(Variance)
什么是方差
方差和標準差是測度數據變異程度的最重要、最常用的指標。
方差是各個數據與其算術平均數的離差平方和的平均數,通常以σ2表示。方差的計量單位和量綱不便于從經濟意義上進行解釋,所以實際統計工作中多用方差的算術平方根——標準差來測度統計數據的差異程度。
標準差又稱均方差,一般用σ表示。方差和標準差的計算也分為簡單平均法和加權平均法,另外,對于總體數據和樣本數據,公式略有不同。
方差的計算公式
設總體方差為σ2,對于未經分組整理的原始數據,方差的計算公式為:
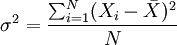
對于分組數據,方差的計算公式為:
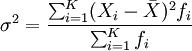
方差的平方根即為標準差,其相應的計算公式為:
未分組數據: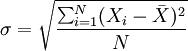
分組數據: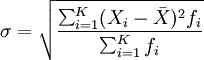
樣本方差和標準差
樣本方差與總體方差在計算上的區別是:總體方差是用數據個數或總頻數去除離差平方和,而樣本方差則是用樣本數據個數或總頻數減1去除離差平方和,其中樣本數據個數減1即n-1稱為自由度。設樣本方差為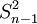 ,根據未分組數據和分組數據計算樣本方差的公式分別為:
,根據未分組數據和分組數據計算樣本方差的公式分別為:
未分組數據: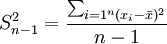
分組數據: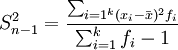
未分組數據: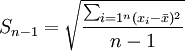
分組數據: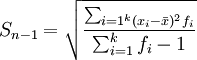
例:考察一臺機器的生產能力,利用抽樣程序來檢驗生產出來的產品質量,假設搜集的數據如下:
| 3.43 |
3.45 |
3.43 |
3.48 |
3.52 |
3.50 |
3.39 |
| 3.48 |
3.41 |
3.38 |
3.49 |
3.45 |
3.51 |
3.50 |
根據該行業通用法則:如果一個樣本中的14個數據項的方差大于0.005,則該機器必須關閉待修。問此時的機器是否必須關閉?
解:根據已知數據,計算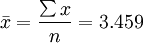
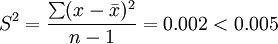
因此,該機器工作正常。
方差和標準差也是根據全部數據計算的,它反映了每個數據與其均值相比平均相差的數值,因此它能準確地反映出數據的離散程度。方差和標準差是實際中應用最廣泛的離散程度測度值。
---------------------------------------------------------------------
http://zh.wikipedia.org/wiki/%E6%96%B9%E5%B7%AE
方差
維基百科,自由的百科全書
在概率論和統計學中,一個隨機變量的“方差”描述的是它的離散程度,也就是該變量離其期望值的距離。 一個實隨機變量的方差也稱為它的二階距,恰巧也是它的二階culmulent。 方差的算術平方根稱為該隨機變量的標準差。
[編輯] 定義
設 X 為服從分布 F 的隨機變量,則稱 Var(X) = E(X − EX)2 為隨機變量 X 或者分布 F 的方差。
如果 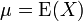 是隨機變數 X 的期望值 (平均數) , 則其變異數為:
是隨機變數 X 的期望值 (平均數) , 則其變異數為: 
[編輯] 特性
在樣本空間Ω上存在有限期望和方差的隨機變量構成一個希爾伯特空間: L^2(Ω, dP),不過這里的內積和長度跟方差,標準差還是不大一樣。 所以,我們得把這個空間“除”常變量構成的子空間,也就是說把相差一個常數的 所有原來那個空間的隨機變量做成一個等價類。這還是一個新的無窮維線性空間, 并且有一個從老空間內積誘導出來的新內積,而這個內積就是方差
[編輯] 一般化
如果X是一個向量其取值范圍在Rn空間,并且其每個元素都是一個一維隨機變量,我們就把X稱為隨機向量。隨機向量的方差是一維隨機變量方差的自然推廣,其定義為E[(X − μ)(X − μ)T], 其中 μ = E(X) ,XT是X的轉秩. 這個方差是一個非負定方陣,通常稱為協方差矩陣。
如果X是一個復隨機變量,那么其方差定義則為E[(X − μ)(X − μ)*], 其中X*是X的復共軛向量。根據這個定義,方差為實數。
[編輯] 歷史
方差這個詞首先由Ronald Fisher在論文The Correlation Between Relatives on the Supposition of Mendelian Inheritance中引入.
[編輯] 參考出處
- ^ Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. (1986) Numerical recipes: The art of scientific computing. Cambridge: Cambridge University Press. (online)
posted on 2009-03-12 22:51
donnie 閱讀(10896)
評論(0) 編輯 收藏 所屬分類:
math