жӯЈжҖҒеҲҶеё?/title><link>http://www.tkk7.com/donnielife/archive/2009/03/12/259454.html</link><dc:creator>donnie</dc:creator><author>donnie</author><pubDate>Thu, 12 Mar 2009 15:08:00 GMT</pubDate><guid>http://www.tkk7.com/donnielife/archive/2009/03/12/259454.html</guid><wfw:comment>http://www.tkk7.com/donnielife/comments/259454.html</wfw:comment><comments>http://www.tkk7.com/donnielife/archive/2009/03/12/259454.html#Feedback</comments><slash:comments>0</slash:comments><wfw:commentRss>http://www.tkk7.com/donnielife/comments/commentRss/259454.html</wfw:commentRss><trackback:ping>http://www.tkk7.com/donnielife/services/trackbacks/259454.html</trackback:ping><description><![CDATA[http://wiki.mbalib.com/wiki/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83<br />
<h1 class="firstHeading">жӯЈжҖҒеҲҶеё?/h1>
<div class="tnbrfzh" id="bodyContent">
<h3 id="siteSub">еҮшҷҮӘMBAжҷәеә“зҷ„Ў§‘(<a >http://wiki.mbalib.com/</a>)</h3>
<div class="pvdhvfp" id="contentSub"></div>
<!-- start content -->
<p><strong>жӯЈжҖҒеҲҶеёғпјҲnormal distribution)</strong> </p>
<table class="toc" id="toc" summary="зӣ®еҪ•">
<tbody>
<tr>
<td>
<div class="vnjxrbr" id="toctitle">
<h2>зӣ®еҪ•</h2>
<span id="xjbvhfx" class="toctoggle">[<a class="internal" id="togglelink" href="javascript:toggleToc()">йҡҗи—Ҹ</a>]</span></div>
<ul lastcheckbox="null">
<li id="jvfhlzp" class="toclevel-1"><a ><span id="rbnxzxx" class="tocnumber">1</span> <span id="bthvhnd" class="toctext">д»Җд№ҲжҳҜжӯЈжҖҒеҲҶеё?/span></a>
<li id="hrvnphn" class="toclevel-1"><a ><span id="ndztnjr" class="tocnumber">2</span> <span id="fxrdndl" class="toctext">жӯЈжҖҒеҲҶеёғзҡ„еҸ‘еұ•</span></a>
<li id="nplhrhp" class="toclevel-1"><a ><span id="zjvzjhn" class="tocnumber">3</span> <span id="dnpbllj" class="toctext">жӯЈжҖҒеҲҶеёғзҡ„дё»иҰҒзү№еҫҒ</span></a>
<li id="xptdfft" class="toclevel-1"><a ><span id="xxtvnnj" class="tocnumber">4</span> <span id="fxrdxnt" class="toctext">жӯЈжҖҒеҲҶеёғзҡ„еә”з”Ё</span></a> </li>
</ul>
</td>
</tr>
</tbody>
</table>
<script type="text/javascript"> if (window.showTocToggle) { var tocShowText = "жҳ„ЎӨә"; var tocHideText = "йҡҗи—Ҹ"; showTocToggle(); } </script>
<div id="tlxhbpj" class="editsection" style="float: right; margin-left: 5px">[<a title="ҫ~–иҫ‘ҢDөиҗҪ: д»Җд№ҲжҳҜжӯЈжҖҒеҲҶеё? >ҫ~–иҫ‘</a>]</div>
<a name=".E4.BB.80.E4.B9.88.E6.98.AF.E6.AD.A3.E6.80.81.E5.88.86.E5.B8.83"></a>
<h2>д»Җд№ҲжҳҜжӯЈжҖҒеҲҶеё?</h2>
<p>гҖҖгҖҖжӯЈжҖҒеҲҶеёғжҳҜдёҖҝUҚжҰӮзҺҮеҲҶеёғгҖӮжӯЈжҖҒеҲҶеёғжҳҜе…дhңүдёӨдёӘеҸӮж•°μе’?#963;2зҡ„иҝһҫlӯеһӢйҡҸжңәеҸҳйҮҸзҡ„еҲҶеёғпјҢҪW¬дёҖеҸӮж•°μжҳҜйҒөд»ҺжӯЈжҖҒеҲҶеёғзҡ„йҡҸжңәеҸҳйҮҸзҡ„еқҮеҖы|јҢҪW¬дәҢдёӘеҸӮж•?#963;2жҳҜжӯӨйҡҸжңәеҸҳйҮҸзҡ„ж–№е·®пјҢжүҖд»ҘжӯЈжҖҒеҲҶеёғи®°дҪңN(μеQ?#963;2 )гҖӮйҒөд»ҺжӯЈжҖҒеҲҶеёғзҡ„йҡҸжңәеҸҳйҮҸзҡ„жҰӮзҺҮ规еҫӢдШ“еҸ?μйӮ»иҝ‘зҡ„еҖјзҡ„жҰӮзҺҮеӨ?еQҢиҖҢеҸ–јӣ?#956;ӯ‘Ҡиҝңзҡ„еҖјзҡ„жҰӮзҺҮӯ‘Ҡе°ҸеQ?#963;ӯ‘Ҡе°ҸеQҢеҲҶеёғи¶ҠйӣҶдёӯең?#956;йҷ„иҝ‘еQ?#963;ӯ‘ҠеӨ§еQҢеҲҶеёғи¶ҠеҲҶж•ЈгҖӮжӯЈжҖҒеҲҶеёғзҡ„еҜҶеәҰеҮҪж•°зҡ„зү№зӮТҺҳҜеQҡе…ідә?#956;еҜ№з§°еQҢеңЁμеӨ„иҫҫеҲ°жңҖеӨ§еҖы|јҢеңЁжӯЈеQҲиҙҹеQүж— ҪIҜӮҝңеӨ„еҸ–еҖйgШ“0еQҢеңЁμ±σеӨ„жңүжӢҗзӮ№гҖӮе®ғзҡ„еЕһзҠ¶жҳҜдёӯй—ҙй«ҳдёӨиҫ№дҪҺ еQҢеӣҫеғҸжҳҜдёҖжқЎдҪҚдәҺx иҪҙдёҠж–№зҡ„<a title="й’ҹеЕһжӣІзәҝ" >й’ҹеЕһжӣІзәҝ</a>гҖӮеҪ“μеQ?еQ?#963;2 еQ?ж—УһјҢҝUоCШ“ж ҮеҮҶжӯЈжҖҒеҲҶеёғпјҢи®оCШ“NеQ?еQ?еQүгҖ?#956;ҫlҙйҡҸжңәеҗ‘йҮҸе…·жңүзұ»дјјзҡ„жҰӮзҺҮ规еҫӢж—УһјҢҝU°жӯӨйҡҸжңәеҗ‘йҮҸйҒөд»ҺеӨҡз»ҙжӯЈжҖҒеҲҶеёғгҖӮеӨҡе…ғжӯЈжҖҒеҲҶеёғжңүеҫҲеҘҪзҡ„жҖ§иҙЁеQҢдҫӢеҰӮпјҢеӨҡе…ғжӯЈжҖҒеҲҶеёғзҡ„иҫ№зјҳеҲҶеёғд»ҚдШ“жӯЈжҖҒеҲҶеёғпјҢе®ғз»Ҹд»ЦMҪ•ҫUҝжҖ§еҸҳжҚўеҫ—еҲ°зҡ„йҡҸжңәеҗ‘йҮҸд»ҚдШ“еӨҡз»ҙжӯЈжҖҒеҲҶеёғпјҢзү№еҲ«е®ғзҡ„ҫUҝжҖ§з»„еҗҲдШ“дёҖе…ғжӯЈжҖҒеҲҶеёғгҖ?</p>
<div id="jvnrjjp" class="editsection" style="float: right; margin-left: 5px">[<a title="ҫ~–иҫ‘ҢDөиҗҪ: жӯЈжҖҒеҲҶеёғзҡ„еҸ‘еұ•" >ҫ~–иҫ‘</a>]</div>
<a name=".E6.AD.A3.E6.80.81.E5.88.86.E5.B8.83.E7.9A.84.E5.8F.91.E5.B1.95"></a>
<h2>жӯЈжҖҒеҲҶеёғзҡ„еҸ‘еұ• </h2>
<p>гҖҖгҖҖжӯЈжҖҒеҲҶеёғжҳҜжңҖйҮҚиҰҒзҡ„дёҖҝUҚжҰӮзҺҮеҲҶеёғгҖӮжӯЈжҖҒеҲҶеёғжҰӮеҝү|ҳҜз”ұеҜdеӣҪзҡ„ж•°еӯҰ家е’ҢеӨ©ж–ҮеӯҰ家Moivreдә?733тqҙеҸ—ӢЖЎжҸҗеҮәзҡ„еQҢдҪҶз”ЧғәҺеҫ·еӣҪж•°еӯҰ家GaussзҺҮе…Ҳһ®Ҷе…¶еә”з”ЁдәҺеӨ©ж–ҮеӯҰе®¶з ”ҪIУһјҢж•…жӯЈжҖҒеҲҶеёғеҸҲеҸ«й«ҳж–ҜеҲҶеёғй«ҳж–Ҝиҝҷҷе№е·ҘдҪңеҜ№еҗҺдё–зҡ„еӘ„е“ҚжһҒеӨ§пјҢд»–дӢЙжӯЈжҖҒеҲҶеёғеҗҢж—¶жңүдә?#8220;й«ҳж–ҜеҲҶеёғ”зҡ„еҗҚҝUҺНјҢеҗҺдё–д№ӢжүҖд»ҘеӨҡһ®ҶжңҖһ®ҸдәҢд№ҳжі•зҡ„еҸ‘жҳҺжқғеҪ’д№ӢдәҺд»–еQҢд№ҹжҳҜеҮәдәҺиҝҷдёҖе·ҘдҪңгҖӮй«ҳж–ҜжҳҜдёҖдёӘдјҹеӨ§зҡ„ж•°еӯҰе®УһјҢйҮҚиҰҒзҡ„иөAзҢ®дёҚиғңжһҡдёҫгҖӮдҪҶзҺоC»Ҡеҫ·еӣҪ10<a title="马е…Ӣ" >马е…Ӣ</a>зҡ„еҚ°жңүй«ҳж–ҜеӨҙеғҸзҡ„й’һзҘЁеQҢе…¶дёҠиҝҳеҚ°жңүжӯЈжҖҒеҲҶеёғзҡ„еҜҶеәҰжӣІзәҝгҖӮиҝҷдј иҫҫдәҶдёҖҝUҚжғіжі•пјҡеңЁй«ҳж–Ҝзҡ„дёҖеҲҮ科еӯҰиөAзҢ®дёӯеQҢе…¶еҜ№дқhҫcАL–ҮжҳҺеӘ„е“ҚжңҖеӨ§иҖ…пјҢһ®ұжҳҜҳqҷдёҖҷеҸVҖӮеңЁй«ҳж–ҜеҲҡдҪңеҮшҷҝҷдёӘеҸ‘зҺоC№ӢеҲқпјҢд№ҹи®ёдәЮZ»¬ҳqҳеҸӘиғҪд»Һе…¶зҗҶи®әзҡ„ҪҺҖеҢ–дёҠжқҘиҜ„д»·е…¶дјҳи¶ҠжҖ§пјҢе…¶е…ЁйғЁеӘ„е“ҚиҝҳдёҚиғҪе……еҲҶзңӢеҮәжқҘгҖӮиҝҷиҰҒеҲ°20дё–зәӘжӯЈжҖҒе°Ҹ<a title="ж дhң¬" >ж дhң¬</a>зҗҶи®әе……еҲҶеҸ‘еұ•иөдhқҘд»ҘеҗҺгҖ?a title="зҡ®еҹғһ®?иҘҝи’ҷ·жӢүжҷ®жӢүж–Ҝ" >зҡ®еҹғһ®?иҘҝи’ҷ·жӢүжҷ®жӢүж–Ҝ</a>еҫҲеҝ«еҫ—зҹҘй«ҳж–Ҝзҡ„е·ҘдҪңпјҢтqүҷ©¬дёҠе°Ҷе…¶дёҺд»–еҸ‘зҺ°зҡ„<a title="дёӯеҝғжһҒйҷҗе®ҡзҗҶ" >дёӯеҝғжһҒйҷҗе®ҡзҗҶ</a>иҒ”зі»иөдhқҘеQҢдШ“жӯӨпјҢд»–еңЁеҚӣ_°ҶеҸ‘иЎЁзҡ„дёҖҪӢҮж–Үз«?еҸ‘иЎЁдә?810тqЯ_јүдёҠеҠ дёҠдәҶдёҖзӮ№иЎҘе……пјҢжҢҮеҮәеҰӮиӢҘиҜҜе·®еҸҜзңӢжҲҗи®ёеӨҡйҮҸзҡ„еҸ еҠ пјҢж ТҺҚ®д»–зҡ„дёӯеҝғжһҒйҷҗе®ҡзҗҶеQҢиҜҜе·®зҗҶеә”жңүй«ҳж–ҜеҲҶеёғгҖӮиҝҷжҳҜеҺҶеҸІдёҠҪW¬дёҖӢЖЎжҸҗеҲ°жүҖи°?#8220;е…ғиҜҜе·®еӯҰиҜ?#8221;вҖ”вҖ”иҜҜе·®жҳҜз”ұеӨ§йҮҸзҡ„гҖҒз”ұҝUҚз§ҚеҺҹеӣ дә§з”ҹзҡ„е…ғиҜҜе·®еҸ еҠ иҖҢжҲҗгҖӮеҗҺжқҘеҲ°1837тqЯ_јҢӢ№дh №(G.Hagen)еңЁдёҖҪӢҮи®әж–ҮдёӯжӯЈејҸжҸҗеҮәдәҶиҝҷдёӘеӯҰиҜҙгҖ?</p>
<p>гҖҖгҖҖе…¶е®һеQҢд»–жҸҗеҮәзҡ„еЕһејҸжңүзӣёеҪ“еӨ§зҡ„еұҖйҷҗжҖ§пјҡӢ№дh №жҠҠиҜҜе·®и®ҫжғПxҲҗдёӘж•°еҫҲеӨҡзҡ„гҖҒзӢ¬з«ӢеҗҢеҲҶеёғзҡ?#8220;е…ғиҜҜе·?#8221; д№Ӣе’ҢеQҢжҜҸеҸӘеҸ–дёӨеҖы|јҢе…¶жҰӮзҺҮйғҪжҳ?/2еQҢз”ұжӯӨеҮәеҸ‘пјҢжҢүзӢ„иҺ«дҪӣзҡ„дёӯеҝғжһҒйҷҗе®ҡзҗҶпјҢз«ӢеҚіһ®ұеҫ—еҮшҷҜҜе·?ҳq‘дјјең?жңҚд»ҺжӯЈжҖҒеҲҶеёғгҖӮзҡ®еҹғе°”-иҘҝи’ҷ·жӢүжҷ®жӢүж–ҜжүҖжҢҮеҮәзҡ„иҝҷдёҖзӮТҺңүйҮҚеӨ§зҡ„ж„Ҹд№үпјҢеңЁдәҺд»–з»ҷиҜҜе·®зҡ„жӯЈжҖҒзҗҶи®ЮZёҖдёӘжӣҙиҮӘ然еҗҲзҗҶгҖҒжӣҙд»ӨдқhдҝЎжңҚзҡ„и§ЈйҮҠгҖӮеӣ дёәпјҢй«ҳж–Ҝзҡ„иҜҙжі•жңүдёҖзӮ№еу@зҺҜи®әиҜҒзҡ„ж°”е‘іеQҡз”ұдәҺз®—жңҜег^еқҮжҳҜдјҳиүҜзҡ„пјҢжҺЁеҮәиҜҜе·®еҝ…йЎ»жңҚд»ҺжӯЈжҖҒеҲҶеёғпјӣеҸҚиҝҮжқҘпјҢз”ұеҗҺдёҖҫl“и®әеҸҲжҺЁеҮәз®—жңҜег^еқҮеҸҠжңҖһ®ҸдәҢд№ҳдј°и®Ўзҡ„дјҳиүҜжҖ§пјҢж•…еҝ…ҷе»и®Өе®ҡиҝҷдәҢиҖ…д№ӢдёҖ(ҪҺ—жңҜтqӣ_қҮзҡ„дјҳиүҜжҖ§пјҢиҜҜе·®зҡ„жӯЈжҖҒжҖ? дёәеҮәеҸ‘зӮ№гҖӮдҪҶҪҺ—жңҜтqӣ_қҮеҲ°еә•тq¶жІЎжңүиҮӘиЎҢжҲҗз«Ӣзҡ„зҗҶз”ұеQҢд»Ҙе®ғдҪңдёәзҗҶи®ЮZёӯдёҖдёӘйў„и®„Ўҡ„еҮәеҸ‘зӮ№пјҢҫlҲи§үжңүе…¶дёҚиғцд№ӢеӨ„гҖӮжӢүжҷ®жӢүж–Ҝзҡ„зҗҶжҠҠҳqҷж–ӯиЈӮзҡ„дёҖзҺҜиҝһжҺҘи“vжқҘпјҢдҪҝд№ӢжҲҗдШ“дёҖдёӘе’Ңи°җзҡ„ж•ҙдҪ“еQҢе®һжңүзқҖжһҒйҮҚеӨ§зҡ„ж„Ҹд№үгҖ?</p>
<div id="xpllxfv" class="editsection" style="float: right; margin-left: 5px">[<a title="ҫ~–иҫ‘ҢDөиҗҪ: жӯЈжҖҒеҲҶеёғзҡ„дё»иҰҒзү№еҫҒ" >ҫ~–иҫ‘</a>]</div>
<a name=".E6.AD.A3.E6.80.81.E5.88.86.E5.B8.83.E7.9A.84.E4.B8.BB.E8.A6.81.E7.89.B9.E5.BE.81"></a>
<h2>жӯЈжҖҒеҲҶеёғзҡ„дё»иҰҒзү№еҫҒ </h2>
<p>гҖҖгҖҖ1гҖҒйӣҶдёӯжҖ§пјҡжӯЈжҖҒжӣІҫUҝзҡ„й«ҳеі°дҪҚдәҺжӯЈдёӯеӨ®пјҢеҚӣ_қҮж•°жүҖеңЁзҡ„дҪҚзҪ®гҖ?</p>
<p>гҖҖгҖҖ2гҖҒеҜ№ҝU°жҖ§пјҡжӯЈжҖҒжӣІҫUҝд»ҘеқҮж•°дёЮZёӯеҝғпјҢе·ҰеҸіеҜ№з§°еQҢжӣІҫUҝдёӨз«Ҝж°ёҳqңдёҚдёҺжЁӘиҪҙзӣёдәӨгҖ?</p>
<p>гҖҖгҖҖ3гҖҒеқҮеҢҖеҸҳеҠЁжҖ§пјҡжӯЈжҖҒжӣІҫUҝз”ұеқҮж•°жүҖеңЁеӨ„ејҖе§ӢпјҢеҲҶеҲ«еҗ‘е·ҰеҸідёӨдҫ§йҖҗжёҗеқҮеҢҖдёӢйҷҚгҖ?</p>
<p>гҖҖгҖҖ4гҖҒжӯЈжҖҒеҲҶеёғжңүдёӨдёӘеҸӮж•°еQҢеҚіеқҮж•°μе’?a title="ж ҮеҮҶе·? >ж ҮеҮҶе·?/a>σеQҢеҸҜи®оCҪңNеQ?#956;еQ?#963;еQүпјҡеқҮж•°μеҶӣ_®ҡжӯЈжҖҒжӣІҫUҝзҡ„дёӯеҝғдҪҚзҪ®еQӣж ҮеҮҶе·®σеҶӣ_®ҡжӯЈжҖҒжӣІҫUҝзҡ„йҷЎеіӯжҲ–жүҒтqізЁӢеәҰгҖ?#963;ӯ‘Ҡе°ҸеQҢжӣІҫUҝи¶ҠйҷЎеіӯеQ?#963;ӯ‘ҠеӨ§еQҢжӣІҫUҝи¶ҠжүҒег^гҖ?</p>
<p>гҖҖгҖҖ5гҖҒuеҸҳжҚўеQҡдШ“дәҶдҫҝдәҺжҸҸҳq°е’Ңеә”з”ЁеQҢеёёһ®ҶжӯЈжҖҒеҸҳйҮҸдҪңж•°жҚ®иҪ¬жҚўгҖ?</p>
<div id="hhldzfv" class="editsection" style="float: right; margin-left: 5px">[<a title="ҫ~–иҫ‘ҢDөиҗҪ: жӯЈжҖҒеҲҶеёғзҡ„еә”з”Ё" >ҫ~–иҫ‘</a>]</div>
<a name=".E6.AD.A3.E6.80.81.E5.88.86.E5.B8.83.E7.9A.84.E5.BA.94.E7.94.A8"></a>
<h2>жӯЈжҖҒеҲҶеёғзҡ„еә”з”Ё </h2>
<p>гҖҖгҖҖ1еQҺдј°и®ЎжӯЈжҖҒеҲҶеёғиө„ж–ҷзҡ„<a title="йў‘ж•°еҲҶеёғ" >йў‘ж•°еҲҶеёғ</a> </p>
<p>гҖҖгҖҖдҫ?.жҹҗең°1993тq?a title="жҠҪж ·и°ғжҹҘ" >жҠҪж ·и°ғжҹҘ</a>дә?00еҗ?8еІҒз”·еӨ§еӯҰз”ҹинnй«ҳпјҲcmеQүпјҢе…¶еқҮж•?172.70cmеQҢж ҮеҮҶе·®s=4.01cmеQҢв‘ дј°и®ЎиҜҘең°18еІҒз”·еӨ§еӯҰз”ҹинnй«ҳеңЁ168cmд»ҘдёӢиҖ…еҚ иҜҘең°18еІҒз”·еӨ§еӯҰз”ҹжҖАL•°зҡ„зҷҫеҲҶж•°еQӣв‘ЎеҲҶеҲ«жұ?a class="image" title="Image:жӯЈжҖҒеҲҶеё?.gif" ><img height="23" alt="Image:жӯЈжҖҒеҲҶеё?.gif" src="http://wiki.mbalib.com/w/images/c/cc/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%831.gif" width="47" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%831.gif" /></a>гҖ?a class="image" title="Image:жӯЈжҖҒеҲҶеё?.gif" ><img height="23" alt="Image:жӯЈжҖҒеҲҶеё?.gif" src="http://wiki.mbalib.com/w/images/5/59/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%832.gif" width="68" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%832.gif" /></a>гҖ?a class="image" title="Image:жӯЈжҖҒеҲҶеё?.gif" ><img height="23" alt="Image:жӯЈжҖҒеҲҶеё?.gif" src="http://wiki.mbalib.com/w/images/6/65/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%833.gif" width="69" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%833.gif" /></a>иҢғеӣҙеҶ?8еІҒз”·еӨ§еӯҰз”ҹеҚ иҜҘең°18еІҒз”·еӨ§еӯҰз”ҹжҖАL•°зҡ„е®һйҷ…зҷҫеҲҶж•°еQҢеЖҲдёҺзҗҶи®әзҷҫеҲҶж•°жҜ”иҫғгҖ?</p>
<p>гҖҖгҖҖжң¬дҫӢеQ?#956;гҖ?#963;жңӘзҹҘдҪҶж ·жң¬еҗ«йҮҸnиҫғеӨ§еQҢжҢүејҸпјҲ3.1еQүз”Ёж дhң¬еқҮж•°<a class="image" title="Image:жӯЈжҖҒеҲҶеё?.gif" ><img height="21" alt="Image:жӯЈжҖҒеҲҶеё?.gif" src="http://wiki.mbalib.com/w/images/c/c7/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%836.gif" width="19" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%836.gif" /></a>е’Ңж ҮеҮҶе·®SеҲҶеҲ«д»Јжӣҝμе’?#963;еQҢжұӮеҫ—uеҖы|јҢu=(168-172.70)/4.01=-1.17гҖӮжҹҘйҷ„иЎЁж ҮеҮҶжӯЈжҖҒжӣІҫUҝдёӢзҡ„йқўҝUҜпјҢеңЁиЎЁзҡ„е·Ұдҫ§жүҫеҲ?1.1еQҢиЎЁзҡ„дёҠж–ТҺүҫеҲ?.07еQҢдёӨиҖ…зӣёдәӨеӨ„дё?.1210=12.10%гҖӮиҜҘең?8еІҒз”·еӨ§еӯҰз”ҹинnй«ҳеңЁ168cmд»ҘдёӢиҖ…пјҢҫUҰеҚ жҖАL•°12.10%гҖӮе…¶е®ғи®ЎҪҺ—з»“жһңи§ҒиЎ?.1гҖ?</p>
<p>гҖҖгҖҖиЎЁпјҡ1100еҗ?8еІҒз”·еӨ§еӯҰз”ҹинnй«ҳзҡ„е®һйҷ…еҲҶеёғдёҺзҗҶи®әеҲҶеё?</p>
<p>гҖҖгҖҖ<a class="image" title="Image:жӯЈжҖҒеҲҶеё?3.jpg" ><img height="113" alt="Image:жӯЈжҖҒеҲҶеё?3.jpg" src="http://wiki.mbalib.com/w/images/3/32/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%8313.jpg" width="346" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%8313.jpg" /></a> </p>
<p>гҖҖгҖҖ2еQҺеҲ¶е®ҡеҢ»еӯҰеҸӮиҖғеҖЖDҢғеӣЯ_јҡдәҰз§°еҢХdӯҰжӯЈеёёеҖЖDҢғеӣҙгҖӮе®ғжҳҜжҢҮжүҖи°?#8220;жӯЈеёёдә?#8221;зҡ„и§Јеү–гҖҒз”ҹзҗҶгҖҒз”ҹеҢ–зӯүжҢҮж Үзҡ„жҮLеҠЁиҢғеӣҙгҖӮеҲ¶е®ҡжӯЈеёёеҖЖDҢғеӣҙж—¶еQҢйҰ–е…ҲиҰҒјӢ®е®ҡдёҖжүТҺ ·жң¬еҗ«йҮҸиғцеӨҹеӨ§зҡ?“жӯЈеёёдә?#8221;еQҢжүҖи°?#8220;жӯЈеёёдә?#8221;дёҚжҳҜжҢ?#8220;еҒҘеә·дә?#8221;еQҢиҖҢжҳҜжҢҮжҺ’йҷӨдәҶеҪұе“ҚжүҖз ”з©¶жҢҮж Үзҡ„з–ҫз—…е’Ңжңүе…іеӣ зҙ зҡ„еҗҢиҙЁдқhҫҹӨпјӣе…¶ж¬ЎйңҖж ТҺҚ®з ”究зӣ®зҡ„е’ҢдӢЙз”ЁиҰҒжұӮйҖүе®ҡйҖӮеҪ“зҡ„зҷҫеҲҶз•ҢеҖы|јҢеҰ?0%еQ?0%еQ?5%е’?9%еQҢеёёз”?5%еQӣж №жҚ®жҢҮж Үзҡ„е®һйҷ…з”ЁйҖ”зЎ®е®ҡеҚ•дҫ§жҲ–еҸҢдҫ§з•ҢеҖы|јҢеҰӮзҷҪҫlҶиғһи®Ўж•°ҳqҮй«ҳҳqҮдҪҺзҡҶеұһдёҚжӯЈеё”RЎ»јӢ®е®ҡеҸҢдҫ§з•ҢеҖы|јҢеҸҲеҰӮиӮқеҠҹдёӯиқ{ж°Ёй…¶ҳqҮй«ҳеұһдёҚжӯЈеёёҷеИқЎ®е®ҡеҚ•дҫ§дёҠз•ҢпјҢиӮәжҙ»йҮҸиҝҮдҪҺеұһдёҚжӯЈеё”RЎ»јӢ®е®ҡеҚ•дҫ§дёӢз•ҢгҖӮеҸҰеӨ–пјҢҳqҳиҰҒж ТҺҚ®иө„ж–ҷзҡ„еҲҶеёғзү№зӮ№пјҢйҖүз”ЁжҒ°еҪ“зҡ„и®ЎҪҺ—ж–№жі•гҖӮеёёз”Ёж–№жі•жңүеQ?</p>
<p>гҖҖгҖҖеQ?еQүжӯЈжҖҒеҲҶеёғжі•еQҡйҖӮз”ЁдәҺжӯЈжҖҒжҲ–ҳq‘дјјжӯЈжҖҒеҲҶеёғзҡ„иө„ж–ҷгҖ?</p>
<p>гҖҖгҖҖеҸҢдҫ§з•ҢеҖы|јҡ<a class="image" title="Image:жӯЈжҖҒеҲҶеё?.gif" ><img height="25" alt="Image:жӯЈжҖҒеҲҶеё?.gif" src="http://wiki.mbalib.com/w/images/b/b6/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%837.gif" width="60" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%837.gif" /></a>еҚ•дҫ§дёҠз•ҢеQ?a class="image" title="Image:жӯЈжҖҒеҲҶеё?.gif" ><img height="25" alt="Image:жӯЈжҖҒеҲҶеё?.gif" src="http://wiki.mbalib.com/w/images/d/d9/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%838.gif" width="60" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%838.gif" /></a>еQҢжҲ–еҚ•дҫ§дёӢз•ҢеQ?a class="image" title="Image:жӯЈжҖҒеҲҶеё?.gif" ><img height="25" alt="Image:жӯЈжҖҒеҲҶеё?.gif" src="http://wiki.mbalib.com/w/images/e/e6/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%839.gif" width="59" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%839.gif" /></a> </p>
<p>гҖҖгҖҖеQ?еQүеҜ№ж•°жӯЈжҖҒеҲҶеёғжі•еQҡйҖӮз”ЁдәҺеҜ№ж•°жӯЈжҖҒеҲҶеёғиө„ж–ҷгҖ?</p>
<p>гҖҖгҖҖеҸҢдҫ§з•ҢеҖы|јҡ<a class="image" title="Image:жӯЈжҖҒеҲҶеё?0.gif" ><img height="27" alt="Image:жӯЈжҖҒеҲҶеё?0.gif" src="http://wiki.mbalib.com/w/images/f/fb/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%8320.gif" width="127" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%8320.gif" /></a>еQӣеҚ•дҫ§дёҠз•Ңпјҡ<a class="image" title="Image:жӯЈжҖҒеҲҶеё?1.gif" ><img height="27" alt="Image:жӯЈжҖҒеҲҶеё?1.gif" src="http://wiki.mbalib.com/w/images/2/27/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%8311.gif" width="127" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%8311.gif" /></a>еQҢжҲ–еҚ•дҫ§дёӢз•ҢеQ?a class="image" title="Image:жӯЈжҖҒеҲҶеё?2.gif" ><img height="27" alt="Image:жӯЈжҖҒеҲҶеё?2.gif" src="http://wiki.mbalib.com/w/images/8/82/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%8312.gif" width="127" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%8312.gif" /></a>гҖ?</p>
<p>гҖҖгҖҖеёёз”ЁuеҖјеҸҜж ТҺҚ®иҰҒжұӮз”ЮpЎЁ3.2жҹҘеҮәгҖ?</p>
<p>гҖҖгҖҖеQ?еQүзҷҫеҲҶдҪҚж•°жі•еQҡеёёз”ЁдәҺеҒҸжҖҒеҲҶеёғиө„ж–ҷд»ҘеҸҠиө„ж–ҷдёӯдёҖз«ҜжҲ–дёӨз«Ҝж— зЎ®еҲҮж•°еҖјзҡ„иө„ж–ҷгҖ?</p>
<p>гҖҖгҖҖеҸҢдҫ§з•ҢеҖы|јҡP2.5е’ҢP97.5еQӣеҚ•дҫ§дёҠз•ҢпјҡP95еQҢжҲ–еҚ•дҫ§дёӢз•ҢеQҡP5гҖ?</p>
<p>гҖҖгҖҖиЎЁпјҡеёёз”ЁuеҖЖDЎЁ </p>
<p>гҖҖгҖҖ<a class="image" title="Image:жӯЈжҖҒеҲҶеё?4.jpg" ><img height="101" alt="Image:жӯЈжҖҒеҲҶеё?4.jpg" src="http://wiki.mbalib.com/w/images/9/91/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%8314.jpg" width="243" longdesc="/wiki/Image:%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%8314.jpg" /></a> </p>
<p>гҖҖгҖҖ3еQҺжӯЈжҖҒеҲҶеёғжҳҜи®ёеӨҡҫlҹи®Ўж–ТҺі•зҡ„зҗҶи®әеҹәјӢҖеQҡеҰӮtеҲҶеёғгҖҒFеҲҶеёғгҖҒеҲҶеёғйғҪжҳҜеңЁжӯЈжҖҒеҲҶеёғзҡ„еҹәзЎҖдёҠжҺЁеҜјеҮәжқҘзҡ„еQҢuӢӮҖйӘҢд№ҹжҳҜд»ҘжӯЈжҖҒеҲҶеёғдШ“еҹәзЎҖзҡ„гҖӮжӯӨеӨ–пјҢtеҲҶеёғгҖҒдәҢҷе№еҲҶеёғгҖҒPoissonеҲҶеёғзҡ„жһҒйҷҗдШ“жӯЈжҖҒеҲҶеёғпјҢеңЁдёҖе®ҡжқЎд»¶дёӢеQҢеҸҜд»ҘжҢүжӯЈжҖҒеҲҶеёғеҺҹзҗҶжқҘеӨ„зҗҶгҖ?</p>
<!-- Tidy found serious XHTML errors --><!-- Saved in parser cache with key wikidb:pcache:idhash:110906-0!1!0!!zh!2!zh and timestamp 20090306045655 -->
<div id="bblxhfn" class="printfooter">жқҘиҮӘ"<a </div>
<div class="vvhjbjh" id="editnotice"> <font color="#999999" size="-1">еҰӮжһңжӮЁи®Өдёәжң¬жқЎзӣ®ҳqҳжңүеҫ…е®Ңе–„пјҢйңҖиҰҒиЎҘе……ж–°еҶ…е®№жҲ–дҝ®ж”ҡw”ҷиҜҜеҶ…е®№пјҢиҜ?a ><strong>ҫ~–иҫ‘жқЎзӣ®</strong></a></font>гҖ?/div>
<br />
<br />
<br />
<br />
-------------------------------------------------------------------------------------<br />
<br />
http://baike.baidu.com/view/45379.html?wtp=tt<br />
<br />
<h1>жӯЈжҖҒеҲҶеё?/h1>
<div id="xrlnhnv" class="text_pic" style="float: right; visibility: visible"><a target="_blank"><img title="" height="103" alt="" src="http://www.tkk7.com/images/blogjava_net/donnielife/e8112b2ad343262b5343c117.jpg" width="139" border="0" /></a></div>
<div class="jbvxrxn" id="lemmaContent">
<div id="jbfprzp" class="bpctrl"></div>
гҖҖгҖҖжӯЈжҖҒеҲҶеё?br />
<div id="vxrjnlb" class="spctrl"></div>
гҖҖгҖҖnormal distribution<br />
<div id="phrlfvl" class="spctrl"></div>
гҖҖгҖҖдёҖҝUҚжҰӮзҺҮеҲҶеёғгҖӮжӯЈжҖҒеҲҶеёғжҳҜе…дhңүдёӨдёӘеҸӮж•°μе’?#963;2зҡ„иҝһҫlӯеһӢйҡҸжңәеҸҳйҮҸзҡ„еҲҶеёғпјҢҪW¬дёҖеҸӮж•°μжҳҜжңҚд»ҺжӯЈжҖҒеҲҶеёғзҡ„йҡҸжңәеҸҳйҮҸзҡ„еқҮеҖы|јҢҪW¬дәҢдёӘеҸӮж•?#963;2жҳҜжӯӨйҡҸжңәеҸҳйҮҸзҡ„ж–№е·®пјҢжүҖд»ҘжӯЈжҖҒеҲҶеёғи®°дҪңN(μеQ?#963;2 )гҖ?жңҚд»ҺжӯЈжҖҒеҲҶеёғзҡ„йҡҸжңәеҸҳйҮҸзҡ„жҰӮзҺҮ规еҫӢдШ“еҸ–дёҺμйӮ»иҝ‘зҡ„еҖјзҡ„жҰӮзҺҮеӨ?еQҢиҖҢеҸ–јӣ?#956;ӯ‘Ҡиҝңзҡ„еҖјзҡ„жҰӮзҺҮӯ‘Ҡе°ҸеQ?#963;ӯ‘Ҡе°ҸеQҢеҲҶеёғи¶ҠйӣҶдёӯең?#956;йҷ„иҝ‘еQ?#963;ӯ‘ҠеӨ§еQҢеҲҶеёғи¶ҠеҲҶж•ЈгҖӮжӯЈжҖҒеҲҶеёғзҡ„еҜҶеәҰеҮҪж•°зҡ„зү№зӮТҺҳҜеQҡе…ідә?#956;еҜ№з§°еQҢеңЁμеӨ„иҫҫеҲ°жңҖеӨ§еҖы|јҢеңЁжӯЈеQҲиҙҹеQүж— ҪIҜӮҝңеӨ„еҸ–еҖйgШ“0еQҢеңЁμ±σеӨ„жңүжӢҗзӮ№гҖӮе®ғзҡ„еЕһзҠ¶жҳҜдёӯй—ҙй«ҳдёӨиҫ№дҪҺ еQҢеӣҫеғҸжҳҜдёҖжқЎдҪҚдәҺxиҪҙдёҠж–№зҡ„й’ҹеЕһжӣІзәҝгҖӮеҪ“μеQ?еQ?#963;2 еQ?ж—УһјҢҝUоCШ“ж ҮеҮҶжӯЈжҖҒеҲҶеёғпјҢи®оCШ“NеQ?еQ?еQүгҖ?#956;ҫlҙйҡҸжңәеҗ‘йҮҸе…·жңүзұ»дјјзҡ„жҰӮзҺҮ规еҫӢж—УһјҢҝU°жӯӨйҡҸжңәеҗ‘йҮҸйҒөд»ҺеӨҡз»ҙжӯЈжҖҒеҲҶеёғгҖӮеӨҡе…ғжӯЈжҖҒеҲҶеёғжңүеҫҲеҘҪзҡ„жҖ§иҙЁеQҢдҫӢеҰӮпјҢеӨҡе…ғжӯЈжҖҒеҲҶеёғзҡ„иҫ№зјҳеҲҶеёғд»ҚдШ“жӯЈжҖҒеҲҶеёғпјҢе®ғз»Ҹд»ЦMҪ•ҫUҝжҖ§еҸҳжҚўеҫ—еҲ°зҡ„йҡҸжңәеҗ‘йҮҸд»ҚдШ“еӨҡз»ҙжӯЈжҖҒеҲҶеёғпјҢзү№еҲ«е®ғзҡ„ҫUҝжҖ§з»„еҗҲдШ“дёҖе…ғжӯЈжҖҒеҲҶеёғгҖ?br />
<div id="zrlnhpn" class="spctrl"></div>
гҖҖгҖҖжӯЈжҖҒеҲҶеёғжңҖж—©з”ұA.ӢӮЈиҺ«еј—еңЁжұӮдәҢҷе№еҲҶеёғзҡ„жёҗиҝ‘е…¬ејҸдёӯеҫ—еҲ°гҖӮC.F.й«ҳж–ҜеңЁз ”ҪI¶жөӢйҮҸиҜҜе·®ж—¶д»ҺеҸҰдёҖдёӘи§’еәҰеҜјеҮЮZәҶе®ғгҖӮP.S.жӢүжҷ®жӢүж–Ҝе’Ңй«ҳж–Ҝз ”ҪI¶дәҶе®ғзҡ„жҖ§иҙЁгҖ?br />
<div id="hjvnrxd" class="spctrl"></div>
гҖҖгҖҖз”ҹдс”дёҺ科еӯҰе®һйӘҢдёӯеҫҲеӨҡйҡҸжңәеҸҳйҮҸзҡ„жҰӮзҺҮеҲҶеёғйғҪеҸҜд»Ҙҳq‘дјјең°з”ЁжӯЈжҖҒеҲҶеёғжқҘжҸҸиҝ°гҖӮдҫӢеҰӮпјҢеңЁз”ҹдә§жқЎд»¶дёҚеҸҳзҡ„жғ…еҶөдёӢпјҢдә§е“Ғзҡ„ејәеҠӣгҖҒжҠ—еҺӢејәеәҰгҖҒеҸЈеҫ„гҖҒй•ҝеәҰзӯүжҢҮж ҮеQӣеҗҢдёҖҝUҚз”ҹзү©дҪ“зҡ„инnй•СқҖҒдҪ“йҮҚзӯүжҢҮж ҮеQӣеҗҢдёҖҝUҚз§Қеӯҗзҡ„йҮҚйҮҸеQӣжөӢйҮҸеҗҢдёҖзү©дҪ“зҡ„иҜҜе·®пјӣеј№зқҖзӮТҺІҝжҹҗдёҖж–№еҗ‘зҡ„еҒҸе·®пјӣжҹҗдёӘең°еҢәзҡ„е№ҙйҷҚж°ҙйҮҸпјӣд»ҘеҸҠзҗҶжғіж°”дҪ“еҲҶеӯҗзҡ„йҖҹеәҰеҲҶйҮҸеQҢзӯүҪ{үгҖӮдёҖиҲ¬жқҘиҜЯ_јҢеҰӮжһңдёҖдёӘйҮҸжҳҜз”ұи®ёеӨҡеҫ®е°Ҹзҡ„зӢ¬з«ӢйҡҸжңәеӣ зҙ еӘ„е“Қзҡ„ҫl“жһңеQҢйӮЈд№Ҳе°ұеҸҜд»Ҙи®ӨдШ“ҳqҷдёӘйҮҸе…·жңүжӯЈжҖҒеҲҶеёғпјҲи§ҒдёӯеҝғжһҒйҷҗе®ҡзҗҶпјүгҖӮд»ҺзҗҶи®әдёҠзңӢеQҢжӯЈжҖҒеҲҶеёғе…·жңүеҫҲеӨҡиүҜеҘҪзҡ„жҖ§иҙЁ еQҢи®ёеӨҡжҰӮзҺҮеҲҶеёғеҸҜд»Ҙз”Ёе®ғжқҘҳq‘дјјеQӣиҝҳжңүдёҖдәӣеёёз”Ёзҡ„жҰӮзҺҮеҲҶеёғжҳҜз”ұе®ғзӣҙжҺҘеҜјеҮәзҡ„еQҢдҫӢеҰӮеҜ№ж•°жӯЈжҖҒеҲҶеёғгҖҒtеҲҶеёғгҖҒFеҲҶеёғҪ{үгҖ?br />
<div id="hhdfxvd" class="spctrl"></div>
гҖҖгҖҖжӯЈжҖҒеҲҶеёғеә”з”ЁжңҖтqҝжіӣзҡ„иҝһҫlӯжҰӮзҺҮеҲҶеёғпјҢе…¶зү№еҫҒжҳҜ“й’?#8221;еҪўжӣІҫUСқҖ?br />
<div id="tjdprpf" class="spctrl"></div>
гҖҖгҖҖfrom http://www.5yiso.cn<br />
<div id="zjtvxnt" class="spctrl"></div>
гҖҖгҖҖ(дёҖ)жӯЈжҖҒеҲҶеё?br />
<div id="bbdzbpn" class="spctrl"></div>
гҖҖгҖҖ1.жӯЈжҖҒеҲҶеё?<br />
<div id="zzbvxnb" class="spctrl"></div>
гҖҖгҖҖиӢ?зҡ„еҜҶеәҰеҮҪж•ҺНјҲйў‘зҺҮжӣІзәҝеQүдШ“жӯЈжҖҒеҮҪж•ҺНјҲжӣІзәҝеQ?br />
<div id="jjvxppn" class="spctrl"></div>
гҖҖгҖҖ(3-1)<br />
<div id="ndnpbjx" class="spctrl"></div>
гҖҖгҖҖеҲҷз§° жңҚд»ҺжӯЈжҖҒеҲҶеёғпјҢи®°еҸ· пҪ?гҖӮе…¶дё?гҖ?жҳҜдёӨдёӘдёҚјӢ®е®ҡеёёж•°еQҢжҳҜжӯЈжҖҒеҲҶеёғзҡ„еҸӮж•°еQҢдёҚеҗҢзҡ„ гҖҒдёҚеҗҢзҡ„ еҜ№еә”дёҚеҗҢзҡ„жӯЈжҖҒеҲҶеёғгҖ?br />
<div id="hpjhdpl" class="spctrl"></div>
гҖҖгҖҖжӯЈжҖҒжӣІҫUҝе‘Ҳй’ҹеһӢеQҢдёӨеӨҙдҪҺеQҢдёӯй—ҙй«ҳеQҢе·ҰеҸӣ_Ҝ№ҝUҺНјҢжӣІзәҝдёҺжЁӘиҪҙй—ҙзҡ„йқўҝUҜжҖИқӯүдә?гҖ?br />
<div id="ddhtnbb" class="spctrl"></div>
гҖҖгҖҖ2еQҺжӯЈжҖҒеҲҶеёғзҡ„зү№еҫҒ<br />
<div id="rrjvxfl" class="spctrl"></div>
гҖҖгҖҖжңҚд»ҺжӯЈжҖҒеҲҶеёғзҡ„еҸҳйҮҸзҡ„йў‘ж•°еҲҶеёғз”ұ гҖ?е®Ңе…ЁеҶӣ_®ҡгҖ?br />
<div id="phrvfdb" class="spctrl"></div>
гҖҖгҖҖ(1) жҳҜжӯЈжҖҒеҲҶеёғзҡ„дҪҚзҪ®еҸӮж•°еQҢжҸҸҳq°жӯЈжҖҒеҲҶеёғзҡ„йӣҶдёӯӯ‘ӢеҠҝдҪҚзҪ®гҖӮжӯЈжҖҒеҲҶеёғд»Ҙ дёәеҜ№ҝU°ибuеQҢе·ҰеҸӣ_®Ңе…ЁеҜ№ҝU°гҖӮжӯЈжҖҒеҲҶеёғзҡ„еқҮж•°гҖҒдёӯдҪҚж•°гҖҒдј—ж•°зӣёеҗҢпјҢеқҮзӯүдә?гҖ?br />
<div id="vnxzbjh" class="spctrl"></div>
гҖҖгҖҖ(2) жҸҸиҝ°жӯЈжҖҒеҲҶеёғиө„ж–ҷж•°жҚ®еҲҶеёғзҡ„јӣАL•ЈҪEӢеәҰеQ?ӯ‘ҠеӨ§еQҢж•°жҚ®еҲҶеёғи¶ҠеҲҶж•ЈеQ?ӯ‘Ҡе°ҸеQҢж•°жҚ®еҲҶеёғи¶ҠйӣҶдёӯгҖ?д№ҹз§°дёәжҳҜжӯЈжҖҒеҲҶеёғзҡ„еҪўзҠ¶еҸӮж•°еQ?ӯ‘ҠеӨ§еQҢжӣІҫUҝи¶ҠжүҒег^еQҢеҸҚд№ӢпјҢ ӯ‘Ҡе°ҸеQҢжӣІҫUҝи¶ҠзҳҰй«ҳгҖ?br />
<div id="xfbvpnl" class="spctrl"></div>
гҖҖгҖҖ(дә?ж ҮеҮҶжӯЈжҖҒеҲҶеё?br />
<div id="rjvpjhv" class="spctrl"></div>
гҖҖгҖҖ1еQҺж ҮеҮҶжӯЈжҖҒеҲҶеёғжҳҜдёҖҝUҚзү№ҢDҠзҡ„жӯЈжҖҒеҲҶеёғпјҢж ҮеҮҶжӯЈжҖҒеҲҶеёғзҡ„μе’?#963;2дё?е’?еQҢйҖҡеёёз”?еQҲжҲ–ZеQүиЎЁҪCәжңҚд»Һж ҮеҮҶжӯЈжҖҒеҲҶеёғзҡ„еҸҳйҮҸеQҢи®°дё?ZпҪһNеQ?еQ?еQүгҖ?br />
<div id="brbvxnd" class="spctrl"></div>
гҖҖгҖҖ2еQҺж ҮеҮҶеҢ–еҸҳжҚўеQҡжӯӨеҸҳжҚўжңүзү№жҖ§пјҡиӢҘеҺҹеҲҶеёғжңҚд»ҺжӯЈжҖҒеҲҶеё?еQҢеҲҷZ=(x-μ)/σ пҪ?N(0,1) һ®ұжңҚд»Һж ҮеҮҶжӯЈжҖҒеҲҶеё?йҖҡиҝҮжҹҘж ҮеҮҶжӯЈжҖҒеҲҶеёғиЎЁһ®ұеҸҜд»ҘзӣҙжҺҘи®ЎҪҺ—еҮәеҺҹжӯЈжҖҒеҲҶеёғзҡ„жҰӮзҺҮеҖ№{ҖӮж•…иҜҘеҸҳжҚўиў«ҝUоCШ“ж ҮеҮҶеҢ–еҸҳжҚўгҖ?br />
<div id="xfzdfll" class="spctrl"></div>
гҖҖгҖҖ3. ж ҮеҮҶжӯЈжҖҒеҲҶеёғиЎЁ<br />
<div id="dvprrrp" class="spctrl"></div>
гҖҖгҖҖж ҮеҮҶжӯЈжҖҒеҲҶеёғиЎЁдёӯеҲ—еҮЮZәҶж ҮеҮҶжӯЈжҖҒжӣІҫUҝдёӢд»?∞еҲ°X(еҪ“еүҚеҖы|јүиҢғеӣҙеҶ…зҡ„йқўз§ҜжҜ”дҫӢ гҖ?<br />
<div id="nvfzjjz" class="spctrl"></div>
гҖҖгҖҖеQҲдёүеQүжӯЈжҖҒжӣІҫUҝдёӢйқўз§ҜеҲҶеёғ<br />
<div id="btfxbpn" class="spctrl"></div>
гҖҖгҖҖ1еQҺе®һйҷ…е·ҘдҪңдёӯеQҢжӯЈжҖҒжӣІҫUҝдёӢжЁӘибuдёҠдёҖе®ҡеҢәй—ҙзҡ„йқўз§ҜеҸҚжҳ иҜҘеҢәй—ҙзҡ„дҫӢж•°еҚ жҖЦMҫӢж•°зҡ„зҷ‘ЦҲҶжҜ”пјҢжҲ–еҸҳйҮҸеҖЖDҗҪеңЁиҜҘеҢәй—ҙзҡ„жҰӮзҺҮпјҲжҰӮзҺҮеҲҶеёғеQүгҖӮдёҚеҗ?иҢғеӣҙеҶ…жӯЈжҖҒжӣІҫUҝдёӢзҡ„йқўҝUҜеҸҜз”Ёе…¬еј?-2и®Ўз®—гҖ?<br />
<div id="bjlxrzx" class="spctrl"></div>
гҖҖгҖҖеQ?-2еQ?br />
<div id="jzdnzfl" class="spctrl"></div>
гҖҖгҖҖгҖ?<br />
<div id="brnfhtr" class="spctrl"></div>
гҖҖгҖҖ2.еҮ дёӘйҮҚиҰҒзҡ„йқўҝUҜжҜ”дҫ?br />
<div id="rhzlvvl" class="spctrl"></div>
гҖҖгҖҖиҪҙдёҺжӯЈжҖҒжӣІҫUҝд№Ӣй—ҙзҡ„йқўз§ҜжҒ’зӯүдә?гҖӮжӯЈжҖҒжӣІҫUҝдёӢеQҢжЁӘиҪҙеҢәй—Я_јҲμ-σеQ?#956;+σеQүеҶ…зҡ„йқўҝUҜдШ“68.27%еQҢжЁӘиҪҙеҢәй—Я_јҲμ-1.96σеQ?#956;+1.96σеQүеҶ…зҡ„йқўҝUҜдШ“95.00%еQҢжЁӘиҪҙеҢәй—Я_јҲμ-2.58σеQ?#956;+2.58σеQүеҶ…зҡ„йқўҝUҜдШ“99.00%гҖ?br />
<div id="tldpzpn" class="spctrl"></div>
гҖҖгҖҖеQҲеӣӣеQүжӯЈжҖҒеҲҶеёғзҡ„еә”з”Ё<br />
<div id="xprdntr" class="spctrl"></div>
гҖҖгҖҖжҹҗдәӣеҢХdӯҰзҺ°иұЎеQҢеҰӮеҗҢиҙЁҫҹӨдҪ“зҡ„инnй«ҳгҖҒзәўҫlҶиғһж•°гҖҒиЎҖҫUўиӣӢзҷҪйҮҸеQҢд»ҘеҸҠе®һйӘҢдёӯзҡ„йҡҸжңшҷҜҜе·®пјҢе‘ҲзҺ°дёәжӯЈжҖҒжҲ–ҳq‘дјјжӯЈжҖҒеҲҶеёғпјӣжңүдәӣжҢҮж ҮеQҲеҸҳйҮҸпјүиҷҪжңҚд»ҺеҒҸжҖҒеҲҶеёғпјҢдҪҶз»Ҹж•°жҚ®иҪ¬жҚўеҗҺзҡ„ж–°еҸҳйҮҸеҸҜжңҚд»ҺжӯЈжҖҒжҲ–ҳq‘дјјжӯЈжҖҒеҲҶеёғпјҢеҸҜжҢүжӯЈжҖҒеҲҶеёғ规еҫӢеӨ„зҗҶгҖӮе…¶дёӯз»ҸеҜТҺ•°иҪ¬жҚўеҗҺжңҚд»ҺжӯЈжҖҒеҲҶеёғзҡ„жҢҮж ҮеQҢиў«ҝUоCШ“жңҚд»ҺеҜТҺ•°жӯЈжҖҒеҲҶеёғгҖ?br />
<div id="dtnxjbx" class="spctrl"></div>
гҖҖгҖҖ1. дј°и®Ўйў‘ж•°еҲҶеёғ дёҖдёӘжңҚд»ҺжӯЈжҖҒеҲҶеёғзҡ„еҸҳйҮҸеҸӘиҰҒзҹҘйҒ“е…¶еқҮж•оCёҺж ҮеҮҶе·®е°ұеҸҜж №жҚ®е…¬ејҸпјҲ3-2еQүдј°и®Ўд“Qж„ҸеҸ–еҖ?иҢғеӣҙеҶ…йў‘ж•°жҜ”дҫӢгҖ?br />
<div id="ndxzjhn" class="spctrl"></div>
гҖҖгҖҖ2. еҲ¶е®ҡеҸӮиҖғеҖЖDҢғеӣ?br />
<div id="djdphxx" class="spctrl"></div>
гҖҖгҖҖеQ?еQүжӯЈжҖҒеҲҶеёғжі• йҖӮз”ЁдәҺжңҚд»ҺжӯЈжҖҒпјҲжҲ–иҝ‘дјјжӯЈжҖҒпјүеҲҶеёғжҢҮж Үд»ҘеҸҠеҸҜд»ҘйҖҡиҝҮиҪ¬жҚўеҗҺжңҚд»ҺжӯЈжҖҒеҲҶеёғзҡ„жҢҮж ҮгҖ?br />
<div id="vblxrzx" class="spctrl"></div>
гҖҖгҖҖеQ?еQүзҷҫеҲҶдҪҚж•°жі• еёёз”ЁдәҺеҒҸжҖҒеҲҶеёғзҡ„жҢҮж ҮгҖӮиЎЁ3-1дёӯдёӨҝUҚж–№жі•зҡ„еҚ•еҸҢдҫ§з•ҢеҖјйғҪеә”зҶҹҫlғжҺҢжҸЎгҖ?br />
<div id="zzjnffv" class="spctrl"></div>
гҖҖгҖҖиЎ?-1 еёёз”ЁеҸӮиҖғеҖЖDҢғеӣҙзҡ„еҲ¶е®ҡ<br />
<div id="fvxrtth" class="spctrl"></div>
гҖҖгҖҖжҰӮзҺҮ<br />
<div id="jzjvxdt" class="spctrl"></div>
гҖҖгҖҖеQ?еQ?жӯЈжҖҒеҲҶеёғжі• зҷ‘ЦҲҶдҪҚж•°жі?br />
<div id="zxjnxvb" class="spctrl"></div>
гҖҖгҖҖеҸҢдҫ§ еҚ?дҫ?еҸҢдҫ§ еҚ•дҫ§<br />
<div id="zfpjntj" class="spctrl"></div>
гҖҖгҖҖдё?йҷ?дё?йҷ?дё?йҷ?дё?йҷ?<br />
<div id="lttxzfv" class="spctrl"></div>
гҖҖгҖҖ90 <br />
<div id="zhblfvt" class="spctrl"></div>
гҖҖгҖҖ95 <br />
<div id="nlnzljh" class="spctrl"></div>
гҖҖгҖҖ99 <br />
<div id="hphbvjz" class="spctrl"></div>
гҖҖгҖҖ3. иҙЁйҮҸжҺ§еҲ¶еQҡдШ“дәҶжҺ§еҲ¶е®һйӘҢдёӯзҡ„жөӢйҮҸпјҲжҲ–е®һйӘҢпјүиҜҜе·®еQҢеёёд»?дҪңдШ“дёҠгҖҒдёӢиӯҰжҲ’еҖы|јҢд»?дҪңдШ“дёҠгҖҒдёӢжҺ§еҲ¶еҖ№{ҖӮиҝҷж ·еҒҡзҡ„дҫқжҚ®жҳҜеQҡжӯЈеёёжғ…еҶөдёӢӢ№ӢйҮҸеQҲжҲ–е®һйӘҢеQүиҜҜе·®жңҚд»ҺжӯЈжҖҒеҲҶеёғгҖ?br />
<div id="dtdfpfd" class="spctrl"></div>
гҖҖгҖҖ4. жӯЈжҖҒеҲҶеёғжҳҜи®ёеӨҡҫlҹи®Ўж–ТҺі•зҡ„зҗҶи®әеҹәјӢҖгҖ?ӢӮҖйӘҢгҖҒж–№е·®еҲҶжһҗгҖҒзӣёе…ӣ_’ҢеӣһеҪ’еҲҶжһҗҪ{үеӨҡҝUҚз»ҹи®Ўж–№жі•еқҮиҰҒжұӮеҲҶжһҗзҡ„жҢҮж ҮжңҚд»ҺжӯЈжҖҒеҲҶеёғгҖӮи®ёеӨҡз»ҹи®Ўж–№жі•иҷҪ然дёҚиҰҒжұӮеҲҶжһҗжҢҮж ҮжңҚд»ҺжӯЈжҖҒеҲҶеёғпјҢдҪҶзӣёеә”зҡ„ҫlҹи®ЎйҮҸеңЁеӨ§ж ·жң¬ж—¶ҳq‘дјјжӯЈжҖҒеҲҶеёғпјҢеӣ иҖҢеӨ§ж дhң¬ж—¶иҝҷдәӣз»ҹи®ЎжҺЁж–ӯж–№жі•д№ҹжҳҜд»ҘжӯЈжҖҒеҲҶеёғдШ“зҗҶи®әеҹәзЎҖзҡ„гҖ?br />
<div id="xnzlnlr" class="spctrl"></div>
гҖҖгҖҖfrom http://www.foodmate.net/lesson/41/3-1.php<br />
<div id="vlpzjjz" class="spctrl"></div>
гҖҖгҖҖдёҖгҖҒжӯЈжҖҒеҲҶеёғзҡ„жҰӮеҝө<br />
<div id="jrlfhfd" class="spctrl"></div>
гҖҖгҖҖз”ЮpЎЁ1.1зҡ„йў‘ж•°иЎЁиө„ж–ҷжүҖҫlҳеҲ¶зҡ„зӣҙж–№еӣҫеQҢеӣҫ3.1еQ?еQүеҸҜд»ҘзңӢеҮәпјҢй«ҳеі°дҪҚдәҺдёӯйғЁеQҢе·ҰеҸідёӨдҫ§еӨ§иҮҙеҜ№ҝU°гҖӮжҲ‘们и®ҫжғ»IјҢеҰӮжһңи§ӮеҜҹдҫӢж•°йҖҗжёҗеўһеӨҡеQҢз»„ҢDөдёҚж–ӯеҲҶҫlҶпјҢзӣҙж–№еӣщNЎ¶з«Ҝзҡ„ҳqһзәҝһ®ЧғјҡйҖҗжёҗеҪўжҲҗдёҖжқЎй«ҳеіоCҪҚдәҺдёӯеӨ®пјҲеқҮж•°жүҖеңЁеӨ„еQүпјҢдёӨдҫ§йҖҗжёҗйҷҚдҪҺдё”е·ҰеҸӣ_Ҝ№ҝUҺНјҢдёҚдёҺжЁӘибuзӣжҖәӨзҡ„е…үж»‘жӣІҫUҝеӣҫ3.1еQ?еQүгҖӮиҝҷжқЎжӣІҫUҝз§°дёәйў‘ж•°жӣІҫUҝжҲ–йў‘зҺҮжӣІзәҝеQҢиҝ‘дјйgәҺж•°еӯҰдёҠзҡ„жӯЈжҖҒеҲҶеёғпјҲnormal distributionеQүгҖӮз”ұдәҺйў‘зҺҮзҡ„жҖХd’Ңдё?00%жҲ?еQҢж•…иҜҘжӣІҫUҝдёӢжЁӘибuдёҠзҡ„йқўз§Ҝдё?00%жҲ?гҖ?br />
<div id="jhrvxnt" class="spctrl"></div>
гҖҖгҖҖеӣ?.1йў‘ж•°еҲҶеёғйҖҗжёҗжҺҘиҝ‘жӯЈжҖҒеҲҶеёғзӨәж„Ҹеӣҫ<br />
<div id="rxhbflr" class="spctrl"></div>
гҖҖгҖҖдёЮZәҶеә”з”Ёж–№дҫҝеQҢеёёеҜТҺӯЈжҖҒеҲҶеёғеҸҳйҮҸXдҪңеҸҳйҮҸеҸҳжҚўгҖ?br />
<div id="nbdfzxx" class="spctrl"></div>
гҖҖгҖҖеQ?.1еQ?br />
<div id="xnzztrj" class="spctrl"></div>
гҖҖгҖҖиҜҘеҸҳжҚўдӢЙеҺҹжқҘзҡ„жӯЈжҖҒеҲҶеёғиқ{еҢ–дШ“ж ҮеҮҶжӯЈжҖҒеҲҶеё?(standard normal distribution)еQҢдәҰҝU°uеҲҶеёғгҖӮuиў«з§°дёәж ҮеҮҶжӯЈжҖҒеҸҳйҮҸжҲ–ж ҮеҮҶжӯЈжҖҒзҰ»е·®пјҲstandard normal deviateеQүгҖ?br />
<div id="vjdxzxn" class="spctrl"></div>
гҖҖгҖҖдәҢгҖҒжӯЈжҖҒеҲҶеёғзҡ„зү№еҫҒеQ?br />
<div id="hxtlfnn" class="spctrl"></div>
гҖҖгҖҖ1еQҺжӯЈжҖҒжӣІҫUҝпјҲnormal curveеQүеңЁжЁӘибuдёҠж–№еқҮж•°еӨ„жңҖй«ҳгҖ?br />
<div id="bzrlxvl" class="spctrl"></div>
гҖҖгҖҖ2еQҺжӯЈжҖҒеҲҶеёғд»ҘеқҮж•°дёЮZёӯеҝғпјҢе·ҰеҸіеҜ№з§°гҖ?br />
<div id="ljlxrnv" class="spctrl"></div>
гҖҖгҖҖ3еQҺжӯЈжҖҒеҲҶеёғжңүдёӨдёӘеҸӮж•°еQҢеҚіеқҮж•°е’Ңж ҮеҮҶе·®гҖӮжҳҜдҪҚзҪ®еҸӮж•°еQҢеҪ“еӣәе®ҡдёҚеҸҳж—УһјҢӯ‘ҠеӨ§еQҢжӣІҫUҝжІҝжЁӘибuӯ‘Ҡеҗ‘еҸіз§»еҠЁпјӣеҸҚд№ӢеQҢи¶Ҡһ®ҸпјҢеҲҷжӣІҫUҝжІҝжЁӘибuӯ‘Ҡеҗ‘е·Ұ移еҠЁгҖӮжҳҜеҪўзҠ¶еҸӮж•°еQҢеҪ“еӣәе®ҡдёҚеҸҳж—УһјҢӯ‘ҠеӨ§еQҢжӣІҫUҝи¶Ҡтqійҳ”еQӣи¶Ҡһ®ҸпјҢжӣІзәҝӯ‘Ҡе°–еіӯгҖӮйҖҡеёёз”ЁиЎЁҪCәеқҮж•оCШ“еQҢж–№е·®дШ“зҡ„жӯЈжҖҒеҲҶеёғгҖӮз”ЁNеQ?еQ?еQүиЎЁҪCәж ҮеҮҶжӯЈжҖҒеҲҶеёғгҖ?br />
<div id="pxhbnlr" class="spctrl"></div>
гҖҖгҖҖ4еQҺжӯЈжҖҒжӣІҫUҝдёӢйқўз§Ҝзҡ„еҲҶеёғжңүдёҖе®ҡ规еҫӢгҖ?<br />
<div id="hjvphfn" class="spctrl"></div>
гҖҖгҖҖе®һйҷ…е·ҘдҪңдёӯпјҢеё”RңҖиҰҒдәҶи§ЈжӯЈжҖҒжӣІҫUҝдёӢжЁӘибuдёҠжҹҗдёҖеҢәй—ҙзҡ„йқўҝUҜеҚ жҖ»йқўҝUҜзҡ„зҷ‘ЦҲҶж•ҺНјҢд»Ҙдҫҝдј°и®ЎиҜҘеҢәй—ҙзҡ„дҫӢж•°еҚ жҖЦMҫӢж•°зҡ„зҷ‘ЦҲҶж•ҺНјҲйў‘ж•°еҲҶеёғеQүжҲ–и§ӮеҜҹеҖЖDҗҪеңЁиҜҘеҢәй—ҙзҡ„жҰӮзҺҮгҖӮжӯЈжҖҒжӣІҫUҝдёӢдёҖе®ҡеҢәй—ҙзҡ„йқўз§ҜеҸҜд»ҘйҖҡиҝҮйҷ„иЎЁ1жұӮеҫ—гҖӮеҜ№дәҺжӯЈжҖҒжҲ–ҳq‘дјјжӯЈжҖҒеҲҶеёғзҡ„иө„ж–ҷеQҢе·ІзҹҘеқҮж•°е’Ңж ҮеҮҶе·®пјҢһ®ұеҸҜеҜ№е…¶йў‘ж•°еҲҶеёғдҪңеҮәжҰӮзәҰдј°и®ЎгҖ?br />
<div id="pxzlvdb" class="spctrl"></div>
гҖҖгҖҖжҹҘйҷ„иЎ?еә”жіЁж„Ҹпјҡв‘ иЎЁдёӯжӣІҫUҝдёӢйқўз§Ҝдё?∞еҲ°uзҡ„е·Ұдҫ§зҜҸи®ЎйқўҝUҜпјӣв‘ЎеҪ“е·ІзҹҘμгҖ?#963;е’ҢXж—¶е…ҲжҢүејҸеQ?.1еQүжұӮеҫ—uеҖы|јҢеҶҚжҹҘиЎЁпјҢеҪ?#956;гҖ?#963;жңӘзҹҘдё”ж ·жң¬еҗ«йҮҸnӯ‘ӣ_ӨҹеӨ§ж—¶еQҢеҸҜз”Ёж ·жң¬еқҮж•°е’Ңж ҮеҮҶе·®SеҲҶеҲ«д»Јжӣҝμе’?#963;еQҢжҢүејҸжұӮеҫ—uеҖы|јҢеҶҚжҹҘиЎЁпјӣв‘ўжӣІҫUҝдёӢеҜ№з§°дә?зҡ„еҢәй—ҙйқўҝUҜзӣёҪ{үпјҢеҰӮеҢәй—Я_јҲ-∞еQ?1.96еQүдёҺеҢәй—ҙеQ?.96еQ?#8734;еQүзҡ„йқўз§ҜзӣёзӯүеQҢв‘ЈжӣІзәҝдёӢжЁӘиҪҙдёҠзҡ„жҖ»йқўҝUҜдШ“100%жҲ?гҖ?br />
<div id="pvfrtbb" class="spctrl"></div>
гҖҖгҖҖжӯЈжҖҒеҲҶеёғжӣІҫUҝдёӢжңүдёүдёӘеҢәй—ҙзҡ„йқўз§Ҝеә”з”ЁиҫғеӨҡеQҢеә”зҶҹи®°еQҡв‘ ж ҮеҮҶжӯЈжҖҒеҲҶеёғж—¶еҢәй—ҙеQ?1,1еQүжҲ–жӯЈжҖҒеҲҶеёғж—¶еҢәй—ҙеQ?#956;-1σ,μ+1σеQүзҡ„йқўз§ҜеҚ жҖ»йқўҝUҜзҡ„68.27%еQӣв‘Ўж ҮеҮҶжӯЈжҖҒеҲҶеёғж—¶еҢәй—ҙеQ?1.96,1.96еQүжҲ–жӯЈжҖҒеҲҶеёғеҢәй—Я_јҲμ-1.96σ,μ+1.96σеQүзҡ„йқўз§ҜеҚ жҖ»йқўҝUҜзҡ„95%еQӣв‘ўж ҮеҮҶжӯЈжҖҒеҲҶеёғж—¶еҢәй—ҙеQ?2.58,2.58еQүжҲ–жӯЈжҖҒеҲҶеёғж—¶еҢәй—ҙеQ?#956;-2.58σ,μ+2.58σеQүзҡ„йқўз§ҜеҚ жҖ»йқўҝUҜзҡ„99%гҖӮеҰӮеӣ?.2жүҖҪCәгҖӮпјҲμ-3σеQүзҡ„йқўз§ҜжҜ”дҫӢдё?9.74%,(μ-2σ)йқўз§ҜжҜ”дҫӢдё?5.44%гҖ?br />
<div id="ljvprff" class="spctrl"></div>
гҖҖгҖҖеӣ?.2 жӯЈжҖҒжӣІҫUҝдёҺж ҮеҮҶжӯЈжҖҒжӣІҫUҝзҡ„йқўз§ҜеҲҶеёғ<br />
</div>
</div>
<img src ="http://www.tkk7.com/donnielife/aggbug/259454.html" width = "1" height = "1" /><br><br><div align=right><a style="text-decoration:none;" href="http://www.tkk7.com/donnielife/" target="_blank">donnie</a> 2009-03-12 23:08 <a href="http://www.tkk7.com/donnielife/archive/2009/03/12/259454.html#Feedback" target="_blank" style="text-decoration:none;">еҸ‘иЎЁиҜ„и®ә</a></div>]]></description></item><item><title>еқҮеҖ?/title><link>http://www.tkk7.com/donnielife/archive/2009/03/12/259449.html</link><dc:creator>donnie</dc:creator><author>donnie</author><pubDate>Thu, 12 Mar 2009 14:55:00 GMT</pubDate><guid>http://www.tkk7.com/donnielife/archive/2009/03/12/259449.html</guid><wfw:comment>http://www.tkk7.com/donnielife/comments/259449.html</wfw:comment><comments>http://www.tkk7.com/donnielife/archive/2009/03/12/259449.html#Feedback</comments><slash:comments>0</slash:comments><wfw:commentRss>http://www.tkk7.com/donnielife/comments/commentRss/259449.html</wfw:commentRss><trackback:ping>http://www.tkk7.com/donnielife/services/trackbacks/259449.html</trackback:ping><description><![CDATA[<h1>http://baike.baidu.com/view/1052684.htm</h1>
<h1> </h1>
<h1>еқҮеҖ?/h1>
<div class="nvhhtrh" id="lemmaContent">
<div id="xnjbvvb" class="bpctrl"></div>
гҖҖгҖҖҫlҹи®ЎеӯҰжңҜиҜӯпјҢдё?#8220;тqӣ_қҮ”еQ?**erageеQүж„Ҹд№үзӣёеҗҢгҖӮдҫӢеҰӮпјҡ lгҖ?гҖ?еQ?0гҖ?0ҳq?дёӘж•°еӯ—зҡ„еқҮеҖјжҳҜ8гҖ?br />
</div>
<img src ="http://www.tkk7.com/donnielife/aggbug/259449.html" width = "1" height = "1" /><br><br><div align=right><a style="text-decoration:none;" href="http://www.tkk7.com/donnielife/" target="_blank">donnie</a> 2009-03-12 22:55 <a href="http://www.tkk7.com/donnielife/archive/2009/03/12/259449.html#Feedback" target="_blank" style="text-decoration:none;">еҸ‘иЎЁиҜ„и®ә</a></div>]]></description></item><item><title>ж–№е·®(Variance) donnie donnie Thu, 12 Mar 2009 14:51:00 GMT http://www.tkk7.com/donnielife/archive/2009/03/12/259448.html http://www.tkk7.com/donnielife/comments/259448.html http://www.tkk7.com/donnielife/archive/2009/03/12/259448.html#Feedback 0 http://www.tkk7.com/donnielife/comments/commentRss/259448.html http://www.tkk7.com/donnielife/services/trackbacks/259448.html
ж–№е·®(Variance)
д»Җд№ҲжҳҜж–№е·®
гҖҖгҖҖж–№е·®е’?a title="ж ҮеҮҶе·? >ж ҮеҮҶе·?/a>жҳҜжөӢеәҰж•°жҚ®еҸҳејӮзЁӢеәҰзҡ„жңҖйҮҚиҰҒгҖҒжңҖеёёз”Ёзҡ„жҢҮж ҮгҖ?
гҖҖгҖҖж–№е·®жҳҜеҗ„дёӘж•°жҚ®дёҺе…?a title="ҪҺ—жңҜтqӣ_қҮж•? >ҪҺ—жңҜтqӣ_қҮж•?/a>зҡ„зҰ»е·®ег^ж–№е’Ңзҡ„ег^еқҮж•°еQҢйҖҡеёёд»?span class="texhtml">σ2 иЎЁзӨәгҖӮж–№е·®зҡ„и®ЎйҮҸеҚ•дҪҚе’ҢйҮҸҫUІдёҚдҫҝдәҺд»?a title="ҫlҸжөҺ" >ҫlҸжөҺж„Ҹд№үдёҠиҝӣиЎҢи§ЈйҮҠпјҢжүҖд»Ҙе®һйҷ?a title="ҫlҹи®Ўе·ҘдҪң" >ҫlҹи®Ўе·ҘдҪңдёӯеӨҡз”Ёж–№е·®зҡ„ҪҺ—жңҜтqПx–№ж №вҖ”вҖ”ж ҮеҮҶе·®жқҘжөӢеә?a title="ҫlҹи®Ўж•°жҚ®" >ҫlҹи®Ўж•°жҚ®зҡ„е·®ејӮзЁӢеәҰгҖ?
гҖҖгҖҖж ҮеҮҶе·®еҸҲҝU°еқҮж–№е·®еQҢдёҖиҲ¬з”ЁσиЎЁзӨәгҖӮж–№е·®е’Ңж ҮеҮҶе·®зҡ„и®Ўз®—д№ҹеҲҶдёәз®ҖеҚ•ег^еқҮжі•е’?a title="еҠ жқғтqӣ_қҮжі? >еҠ жқғтqӣ_қҮжі?/a>еQҢеҸҰеӨ–пјҢеҜ№дәҺжҖЦMҪ“ж•°жҚ®е’Ңж ·жң¬ж•°жҚ®пјҢе…¬ејҸз•ҘжңүдёҚеҗҢгҖ?
ж–№е·®зҡ„и®ЎҪҺ—е…¬еј?
гҖҖгҖҖи®ҫжҖЦMҪ“ж–№е·®дё?span class="texhtml">σ2 еQҢеҜ№дәҺжңӘҫlҸеҲҶҫl„ж•ҙзҗҶзҡ„еҺҹе§Ӣж•°жҚ®еQҢж–№е·®зҡ„и®Ўз®—е…¬ејҸдёәпјҡ
гҖҖгҖҖ
гҖҖгҖҖеҜ№дәҺеҲҶз»„ж•°жҚ®еQҢж–№е·®зҡ„и®Ўз®—е…¬ејҸдёәпјҡ
гҖҖгҖҖ
гҖҖгҖҖж–№е·®зҡ„ег^ж–ТҺ №еҚідШ“ж ҮеҮҶе·®пјҢе…¶зӣёеә”зҡ„и®Ўз®—е…¬ејҸдёәпјҡ
гҖҖгҖҖжңӘеҲҶҫl„ж•°жҚ®пјҡ
гҖҖгҖҖеҲҶз»„ж•°жҚ®еQ?img class="tex" alt="\sigma=\sqrt{\frac{\sum_{i=1}^K(X_i-\bar{X})^2 f_i}{\sum_{i=1}^K f_i}}" src="http://wiki.mbalib.com/w/images/math/2/c/0/2c033a4986d1f7dec42e6a77383cdd63.png" />
ж дhң¬ж–№е·®е’Ңж ҮеҮҶе·®
гҖҖгҖҖж дhң¬ж–№е·®дёҺжҖЦMҪ“ж–№е·®еңЁи®ЎҪҺ—дёҠзҡ„еҢәеҲ«жҳҜеQҡжҖЦMҪ“ж–№е·®жҳҜз”Ёж•°жҚ®дёӘж•°жҲ–жҖ»йў‘ж•°еҺ»йҷӨзҰ»е·®ег^ж–№е’ҢеQҢиҖҢж ·жң¬ж–№е·®еҲҷжҳҜз”Ёж дhң¬ж•°жҚ®дёӘж•°жҲ–жҖ»йў‘ж•°еҮҸ1еҺ»йҷӨјӣХd·®тqПx–№е’ҢпјҢе…¶дёӯж дhң¬ж•°жҚ®дёӘж•°еҮ?еҚіnеQ?ҝUоCШ“иҮӘз”ұеәҰгҖӮи®ҫж дhң¬ж–№е·®дё?img class="tex" alt="S_{n-1}^2" src="http://wiki.mbalib.com/w/images/math/9/a/c/9ac015d3e4cc254fe214570a638dcff6.png" />еQҢж №жҚ®жңӘеҲҶз»„ж•°жҚ®е’ҢеҲҶҫl„ж•°жҚ®и®ЎҪҺ—ж ·жң¬ж–№е·®зҡ„е…¬ејҸеҲҶеҲ«дёәпјҡ
гҖҖгҖҖжңӘеҲҶҫl„ж•°жҚ®пјҡ
гҖҖгҖҖеҲҶз»„ж•°жҚ®еQ?img class="tex" alt="S_{n-1}^2=\frac{\sum_{i=1^k(x_i-\bar{x})^2 f_i}}{\sum_{i=1}^k f_i-1}" src="http://wiki.mbalib.com/w/images/math/9/b/4/9b46d85cb0f3e684daa53f0d953bfdec.png" />
гҖҖгҖҖжңӘеҲҶҫl„ж•°жҚ®пјҡ
гҖҖгҖҖеҲҶз»„ж•°жҚ®еQ?img class="tex" alt="S_{n-1}=\sqrt{\frac{\sum_{i=1^k(x_i-\bar{x})^2 f_i}}{\sum_{i=1}^k f_i-1}}" src="http://wiki.mbalib.com/w/images/math/8/7/5/8751d577a53ecea6d425af87f6e65948.png" />
гҖҖгҖҖдҫ?иҖғеҜҹдёҖеҸ°жңәеҷЁзҡ„з”ҹдс”иғҪеҠӣ еQҢеҲ©з”ЁжҠҪж пLЁӢеәҸжқҘӢӮҖйӘҢз”ҹдә§еҮәжқҘзҡ„дә§е“ҒиҙЁйҮҸ еQҢеҒҮи®ҫжҗңйӣҶзҡ„ж•°жҚ®еҰӮдёӢеQ?
3.43
3.45
3.43
3.48
3.52
3.50
3.39
3.48
3.41
3.38
3.49
3.45
3.51
3.50
гҖҖгҖҖж ТҺҚ®иҜҘиЎҢдёҡйҖҡз”Ёжі•еҲҷеQҡеҰӮжһңдёҖдёӘж ·жң¬дёӯзҡ?4дёӘж•°жҚ®йЎ№зҡ„ж–№е·®еӨ§дә?.005еQҢеҲҷиҜҘжңәеҷЁеҝ…ҷеХd…ій—ӯеҫ…дҝ®гҖӮй—®жӯӨж—¶зҡ„жңәеҷЁжҳҜеҗҰеҝ…ҷеХd…ій—ӯпјҹ
гҖҖгҖҖи§Јпјҡж ТҺҚ®е·ІзҹҘж•°жҚ®еQҢи®ЎҪҺ?img class="tex" alt="\bar{x}=\frac{\sum x}{n}=3.459" src="http://wiki.mbalib.com/w/images/math/8/e/3/8e3203f72078213f1b654218feaa8297.png" />
гҖҖгҖҖ
гҖҖгҖҖеӣ жӯӨеQҢиҜҘжңәеҷЁе·ҘдҪңжӯЈеёёгҖ?
гҖҖгҖҖж–№е·®е’Ңж ҮеҮҶе·®д№ҹжҳҜж ТҺҚ®е…ЁйғЁж•°жҚ®и®Ўз®—зҡ„пјҢе®ғеҸҚжҳ дәҶжҜҸдёӘж•°жҚ®дёҺе…¶еқҮеҖјзӣёжҜ”ег^еқҮзӣёе·®зҡ„ж•°еҖы|јҢеӣ жӯӨе®ғиғҪеҮҶзЎ®ең°еҸҚжҳ еҮәж•°жҚ®зҡ?a title="јӣАL•ЈҪEӢеәҰ" >јӣАL•ЈҪEӢеәҰгҖӮж–№е·®е’Ңж–№е·®
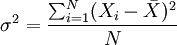
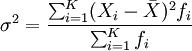
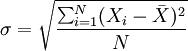
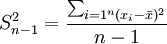
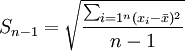
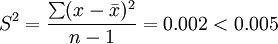
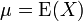 жҳҜйҡЁҠҷҹи®Ҡж•?X зҡ?a title="жңҹжңӣеҖ? >жңҹжңӣеҖ?/a> (тqӣ_қҮж•? , еүҮе…¶и®Ҡз•°ж•ёзӮә:
жҳҜйҡЁҠҷҹи®Ҡж•?X зҡ?a title="жңҹжңӣеҖ? >жңҹжңӣеҖ?/a> (тqӣ_қҮж•? , еүҮе…¶и®Ҡз•°ж•ёзӮә: 