問題的背景是在大數據沖擊下,很多數據指標(尤其是涉及到去重的)的計算無法在合理的空間和時間內完成,比如uv的計算,數學原型問題等價于持續的向一個集合中寫數,重復的不記,要求最終給出集合中不重復的元素的個數(集合的勢)。而比較暴力的做法是隨著數字增多不斷的擴展集合的大小,讓它放下所有的數,最終數出這個個數就OK。顯然這樣的空間復雜度在單機下是做不到的,所以多數做法是利用分布式原理將uv數據隔離到不同的計算節點,每個計算節點自行維護一個類似這樣的集合(wdm實時里的布隆過濾器),然后分而治之,最后merge為一份結果數據。
基數估計的初衷就是為了解決在大數據的前提下,如何以低成本的空間復雜度去計算超大集合的勢的問題,換句話說,通過基數估計,單機做到計算億級別uv,誤差在4%以內。解決思路主要是概率估計,具體原理和做法參看 blog和論文原文。
出于實驗的目的,我簡單實現了暴力做法bruteforce-bf,布隆過濾器-bbf,loglog-llc和hyperloglog-hllc四個算法,比較一下基數估計這個計算去重指標的邏輯是否可行(llc非常離譜,可能是我分桶數沒有調整好,就不貼出結果了)。
預處理方法:1-N生成隨機uid,模擬N次(均勻分布),jvm啟動-Xmx1024m。
實驗結果:
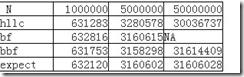
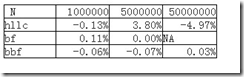
附加說明一下,期望值如何計算:其實這個實驗的數學原型就是一個長度為k的均勻分布的(1-N)的隨機數列,求不重復的元素個數的期望。我實驗里k=n,這是一種極端情況(實驗設計純為方便計算,如果k較大會導致計算超慢,uv5000w時根本無法計算出來,增大k理論上會提高精度,我實驗過的一組數據是100w uv 500wpv時 hllc的值是991234,誤差<1%),理論上k相當于pv,在遞推公式中k趨于無窮時期望等于n。
這個遞推的計算可以通過組合分析推導,推導方法不詳說了(當然我有可能推導錯了~~數學功底 實在 不行了),通項公式見matlab代碼。
syms e n;
e = n-(1/n)*((1-2*n+n*n)*((n-1)/n)^(n-2)+(1-n)*n+n*(n-1));
vpa(subs(e,'n',1000000),10)
另外,我個人認為分布式布隆過濾器的方案是非常好的,因為空間和時間都比較均衡,且精確度高,基數估計的方法本質上空間復雜度O(1),時間復雜度代碼高效一點也可以非常快,但是缺點是精確度稍微欠缺,且不易分布式計算(因為它天生適合單進程,llc分桶均衡也是單進程做比較好,分布式完全是牛刀殺雞)。
ref blog: http://blog.codinglabs.org/articles/cardinality-estimate-exper.html#ref4
算法實現的java代碼可見github: https://github.com/changedi/card-estimate