Change Dir

Logistic Regression——用線解決問題

LR一般用于預(yù)測(cè)二分類問題，即yes no和0\1問題，我們構(gòu)建了X(設(shè)備屬性和行為屬性)，我們需要預(yù)測(cè)Y(是否異常)，而反作弊項(xiàng)目中，我們需要預(yù)測(cè)的就是設(shè)備作弊o(hù)r正常,即0\1問題。選擇LR一個(gè)很重要的原因是我們相信X和Y是有聯(lián)系的，不同的類型的Y會(huì)有不同的X表現(xiàn)。

而X和Y是否有線性關(guān)系？ 普通線性回歸(Ordinary Linear Regression)是否就能滿足需求？我們需要先論證這個(gè)問題，我們看一下普通線性回歸，模型是這樣的：

在線性回歸中，隨機(jī)誤差項(xiàng)服從正態(tài)分布。這也意味著回歸的Y值是個(gè)連續(xù)變量，不能是0\1這樣的binary變量。另外一個(gè)解釋就是線性回歸對(duì)響應(yīng)變量Y的要求是有常數(shù)方差，這也限定了Y的分布，就比如二項(xiàng)分布的Y就沒有常數(shù)方差。這也正符合我們常規(guī)的閱讀理解，回歸用于定量分析，更多的在擬合和預(yù)測(cè)量上，而分類是個(gè)定性分析。正因?yàn)镺LR的做法限制太多，因此有了通用線性回歸的方法（General Linear Regression），通用方法的思路就是尋求一個(gè)轉(zhuǎn)換函數(shù)g來作用于輸入變量X，從而擺脫對(duì)Y的分布限制。具體表現(xiàn)為

下面兩張圖對(duì)比了線性回歸和邏輯回歸數(shù)據(jù)的特點(diǎn)，也說明了如果用線性回歸來分類binary數(shù)據(jù)是一個(gè)什么樣的效果。

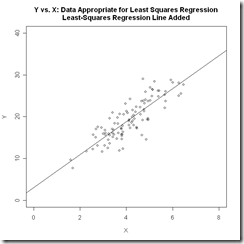
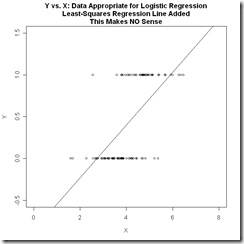
其實(shí)比較樸素的理解就是，我們把要分類的數(shù)據(jù)劃分為0和1兩類，那么數(shù)據(jù)其實(shí)是會(huì)以中間這幅圖的形式分布的，必然存在一個(gè)平面（直線）把數(shù)據(jù)劃分。而我們希望找到一個(gè)判別函數(shù)能完成區(qū)分，顯而易見的是直線無法完成這個(gè)事情。

面對(duì)線性回歸的劣勢(shì)，我們理解回歸的問題在于無法對(duì)公式（1）的結(jié)果做0\1劃分，線性回歸的方法做分類，就是要求

而邏輯回歸作為GLR的一個(gè)特殊情況，定義了一函數(shù)f()，這個(gè)函數(shù)可以將Y做0\1處理，從而使線性回歸變得有意義。而邏輯回歸的做法就是找到了這樣一個(gè)函數(shù)，這個(gè)函數(shù)也叫l(wèi)ogit函數(shù)

其中我們把p等價(jià)于原來的 ，解釋一下就是p代表Y=1的概率，標(biāo)準(zhǔn)說法p是Y=1時(shí)Y的期望。然后把這個(gè)p替換掉就得到了

目標(biāo)是求解，于是

這里就不是一個(gè)線性函數(shù)了，上面提到的公式（2）對(duì)應(yīng)的曲線上面最右邊的圖——可以看到p的函數(shù)曲線，這樣的劃分對(duì)于0\1數(shù)據(jù)的分類是非常合適的。

那么一個(gè)問題就隨之而來，logit函數(shù)是怎么來的？要想知道答案，我們需要先分析一下這個(gè)形式，我們定義這個(gè)形式為“優(yōu)勢(shì)”（odds），odds有時(shí)候也叫做“幾率”，odds的函數(shù)形式其實(shí)是下面左圖的樣子，而logit函數(shù)的形式是右圖的樣子

odds的理解其實(shí)要結(jié)合概率的思想，我們認(rèn)為一個(gè)事件發(fā)生的概率是p，那么不發(fā)生的概率就是1-p，而odds表達(dá)的就是事件發(fā)生與不發(fā)生（或者一個(gè)標(biāo)注yes 或者no）的幾率，比如一個(gè)事情發(fā)生的概率是0.9，而不發(fā)生是0.1，那么odds（發(fā)生）=0.9/0.1=9，而odds(不發(fā)生)=0.1/0.9=0.1111...。這說明一種事物相比較時(shí)的優(yōu)勢(shì)，但是這個(gè)優(yōu)勢(shì)在形式上非對(duì)稱，這樣是不完美的，也是難于理解的，畢竟對(duì)于一個(gè)0-1之間的概率比較，結(jié)果卻在0-∞之間。而可以看出logit函數(shù)是把odds對(duì)數(shù)化后得到的一個(gè)對(duì)稱的美妙的曲線，擁有我們想要的所有性質(zhì)，并且解決了OLR所限制的問題，而且由公式（3）我們也能看到，logit函數(shù)使結(jié)果限定在0-1之間，且是輸入變量X的線性表示。

最后當(dāng)我們計(jì)算出p，我們就能確定分類，比如p>0.5時(shí) y=1，而p<0.5時(shí)y=0。于是這樣的分類任務(wù)就結(jié)束了。不過我們?cè)倏纯茨Ｐ停坪跬浟耸裁矗覀兛梢詮臄?shù)據(jù)集里得到X和Y，但是對(duì)于α和β以及ε的值（參數(shù)值），我們需要獲取到。而這才是LR作為機(jī)器學(xué)習(xí)方法最關(guān)鍵的一個(gè)部分。

我們假設(shè)數(shù)據(jù)集有n個(gè)數(shù)據(jù)樣本，且n大于估計(jì)的參數(shù)的個(gè)數(shù)，于是我們令

我們用β表示整個(gè)參數(shù)向量，那么原來的表達(dá)式可以寫為Y=X*β。類似最小二乘法的思路，我們有下面的推斷

其實(shí)如果把目標(biāo)約定為計(jì)算β,那么問題也就被歸約為一個(gè)參數(shù)估計(jì)問題，而我們最常用的方法就是極大似然估計(jì)法。這里不具體介紹MLE，換種角度我們從頭開始設(shè)計(jì)這個(gè)分類器。

之前考慮的點(diǎn)我們簡化了分析，我們理所當(dāng)然的認(rèn)為X特征向量彼此是同等重要的，而事實(shí)往往不是這樣，因此模型需要加入一個(gè)權(quán)重影響因子，也就是LR模型被擴(kuò)展為Weighted Logistic Regression，因?yàn)槟繕?biāo)是計(jì)算公式（5），加入權(quán)重后，我們把評(píng)估公式（5）的做法替換為去評(píng)估

這里就涉及一個(gè)問題：權(quán)重具體是個(gè)什么定義？權(quán)重W是個(gè)對(duì)角矩陣，其對(duì)角元素即每個(gè)特征項(xiàng)的權(quán)重值，而這個(gè)權(quán)重定義為預(yù)測(cè)變量的標(biāo)準(zhǔn)差。此時(shí)我們回到一個(gè)基本問題，LR用來預(yù)測(cè)二類問題，而我們一般假設(shè)我們的預(yù)測(cè)變量Y是服從二項(xiàng)分布的即，那么方差，更特殊的，對(duì)于單次試驗(yàn)是伯努利分布，所以有，而這個(gè)即我們對(duì)于預(yù)測(cè)變量Y的估計(jì)值，形如公式（4），換用現(xiàn)在對(duì)β的定義就是，回到公式（6）中，我們新引入的變量U即表示為，其中后面這個(gè)加項(xiàng)我們這么理解：分子是一個(gè)預(yù)測(cè)誤差項(xiàng)，而分母是我們定義的權(quán)重，這樣一個(gè)比值縮放了正確分類的大方差樣本點(diǎn)和小方差樣本點(diǎn)對(duì)結(jié)果的影響。另外需要引入的一個(gè)概念是嶺回歸（Ridge Regression），源于一些預(yù)測(cè)變量y可能是線性相關(guān)的，那么這會(huì)導(dǎo)致是奇異矩陣，會(huì)導(dǎo)致無窮解，因此在帶求解的公式（6）的基礎(chǔ)上，為可逆矩陣引入一個(gè)常量對(duì)角矩陣，公式變?yōu)?

其中是小常量，而I是單位矩陣。這樣做避免了對(duì)奇異矩陣求逆，但是帶來了問題就是對(duì)預(yù)測(cè)變量結(jié)果的偏置，導(dǎo)致目標(biāo)問題發(fā)生了小小的變化。多種方法可以幫助我們尋找一個(gè)好的，這里就不具體展開了，具體參考資料即可。

最后就是算法實(shí)現(xiàn)了，為了避免復(fù)雜的矩陣求逆，我們把形式變一下，將公式（7）轉(zhuǎn)換為求解這樣一個(gè)線性系統(tǒng)

其中，。可以看出，算法的輸入是特征矩陣X和U（間接得到），輸出是β。求解線性系統(tǒng)的算法有很多，其中共軛梯度算法是非常有效的算法，下面左圖描述了共軛梯度算法的實(shí)現(xiàn)偽代碼。

共軛梯度：

IRLS：

其中值得一提的是共軛梯度算法中的“is large enough”或者維基上說的“sufficiently small”有多種判斷方式，具體這里就不列出了，可以看參考資料[2]。右圖是迭代重加權(quán)最小二乘法，用于最終求解β。

我在github上放了一個(gè)《machine learning in action》中的LR算法的python實(shí)現(xiàn)，對(duì)于β的求解使用的是梯度下降法，可以參考https://github.com/changedi/mlmlml/blob/master/LogisticRegression/logRegres.py，而關(guān)于梯度下降等最優(yōu)化算法，我想還是單獨(dú)開一篇去介紹比較合適。至此，LR的基本介紹基本就結(jié)束了。

文中除流程圖外，其他截圖取自ref[2]，特此聲明。

References:

[1] http://logisticregressionanalysis.com/86-what-is-logistic-regression/

[2] http://www.omidrouhani.com/research/logisticregression/html/logisticregression.htm

[3] 《統(tǒng)計(jì)學(xué)習(xí)方法》，李航

[4] Logit Models for Binary Data, G. Rodriguez, 2007

[5] http://zh.wikipedia.org/wiki/%E5%85%B1%E8%BD%AD%E6%A2%AF%E5%BA%A6%E6%B3%95

[6] http://cnx.org/content/m45285/latest/

posted on 2014-08-05 09:38 changedi 閱讀(4326) 評(píng)論(1)  編輯  收藏 所屬分類: 機(jī)器學(xué)習(xí) 、數(shù)學(xué)