算法導論第27章,在并行處理的條件下效率很高的排序算法。
介紹如下面左圖所示,每條橫線(wire)代表一個待比較的數值,豎線(comparator)表示連接的兩條橫線要做一次比較,并將較小的值放在輸出橫線的上方,較大的放在下面。排序過程就是從左往右依次調用各個comparator(在同一位置上的comparator可以同時做)
有圖表示了四個數字3, 2, 4, 1在經過這個Sorting Network時的行為。

下圖是一個冒泡排序的Sorting Network表示

可以看到所有的比較都沒有并行,效率很低。接下來先介紹一個0-1原理,然后利用它來構造一些比較高效的網絡。
性質首先是引理27.1:
對于輸入數據A = <a_1, a_2, .., a_n>,如果某個比較網絡(comparison network)的輸出是B = <b_1, b_2, ..., b_n>,那么對于任一單調遞增的函數f,這個網絡能把輸入數據f(A) = <f(a_1), f(a_2), ..., f(a_n)>變為f(B) = <f(b_1), f(b_2), ...f(b_3)>
這個引理的證明很簡單,關鍵在于min(f(x), f(y)) = f(min(x,y))
接下來就是0-1原理:
一個有n個輸入數據的比較網絡,如果它能將僅由0和1組成的序列正確的排序(這種輸入共有2^n種可能),那么它也能正確的將任意數字組成的序列排序。
證明也不難,利用前面的引理反正即可得到這個定理。
雙調排序接下來先考慮雙調序列(bitonic sequence)這種特殊情況,所謂雙調序列就是先單調遞增,后單調遞減,或者可以通過環形旋轉變化出上述特性的序列,比如<1, 4, 6, 8, 3, 2>和<6, 9, 4, 2, 3, 5>都滿足條件(對于后面一種序列,只要把最后的3, 5移到序列開頭就行了)。
雙調排序(bitonic sorter)有若干步驟,其中有一步叫做half-cleaner,每一次half-cleaner講數據放到一個深度為1的排序網絡中,第i行和第i+n/2行比較(i=1,2,..,n/2)

引理27.3:
做完上述的half-cleaner后,輸出的上半部分和下半部分都保持雙調的特點,而且上半部分的每個元素都不大于下半部分的任一元素。
分四種情況討論即可。
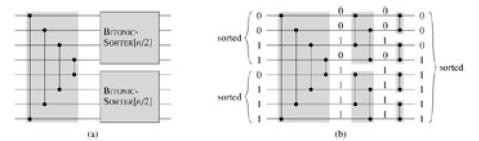
通過遞歸調用half-cleaner即可完成雙調隊列的排序。要對n個元素進行雙調排序Bitonic-Sorter(n),首先調用Half-Cleaner(n),將元素分成上下兩部分,接著依次對這兩部分執行Bitonic-Sorter(n/2)即可。
調用的深度D(n) = lgn
歸并網絡
書上只給出了對0-1序列排序的算法,任意數字的排序算法留作了習題。
合并網絡基于這樣一個事實:對于兩個已經排序了的序列X = 00000111,Y = 00001111,將Y倒過來后和X拼接的結果是一個雙調序列。對這個雙調序列再做一次Bitonic-Sorter就能有序。
通過修改Bitonic-Sorter方法的第一步就能實現Merger,關鍵在于隱式的反轉輸入的下半部分。Half-Cleaner方法中比較了第i和第i+n/2兩個元素,如果下半部分反轉的話就相當于比較第i和第n-i+1個元素。直接繼續執行Bitonic-Sorter方法即可,如下圖所示。
 排序網絡
排序網絡我們已經有了構造一個排序網絡所需的工具,接下來介紹一種利用歸并網絡進行排序的并行版本。
大致方法和傳統的歸并排序類似,從最小的顆粒開始二分增長,直到整個序列有序。
這樣,一共需要lg(n)次Merger,每次歸并中需要做lg(i)次Sorter,排序的總深度
D(n) =
0 ? ? ? ? ? ? ? (n = 1)
D(n/2) + lg(n)? (n = 2^k且 k>=1)
由Master Method可推出D(n) = big-omega(lg^2(n))
也就是說理想的并行環境中,n個數可以在O(lg^2(n))時間內完成排序。
Bitonic Sorter http://www.iti.fh-flensburg.de/lang/algorithmen/sortieren/bitonic/bitonicen.htm