xylz,imxylz

在上一篇中介紹了HashMap的原理，這一節(jié)是ConcurrentMap的最后一節(jié)，所以會(huì)完整的介紹ConcurrentHashMap的實(shí)現(xiàn)。

ConcurrentHashMap原理

在讀寫鎖章節(jié)部分介紹過一種是用讀寫鎖實(shí)現(xiàn)Map的方法。此種方法看起來可以實(shí)現(xiàn)Map響應(yīng)的功能，而且吞吐量也應(yīng)該不錯(cuò)。但是通過前面對讀寫鎖原理的分析后知道，讀寫鎖的適合場景是讀操作>>寫操作，也就是讀操作應(yīng)該占據(jù)大部分操作，另外讀寫鎖存在一個(gè)很嚴(yán)重的問題是讀寫操作不能同時(shí)發(fā)生。要想解決讀寫同時(shí)進(jìn)行問題（至少不同元素的讀寫分離），那么就只能將鎖拆分，不同的元素?fù)碛胁煌逆i，這種技術(shù)就是“鎖分離”技術(shù)。

默認(rèn)情況下ConcurrentHashMap是用了16個(gè)類似HashMap 的結(jié)構(gòu)，其中每一個(gè)HashMap擁有一個(gè)獨(dú)占鎖。也就是說最終的效果就是通過某種Hash算法，將任何一個(gè)元素均勻的映射到某個(gè)HashMap的Map.Entry上面，而對某個(gè)一個(gè)元素的操作就集中在其分布的HashMap上，與其它HashMap無關(guān)。這樣就支持最多16個(gè)并發(fā)的寫操作。

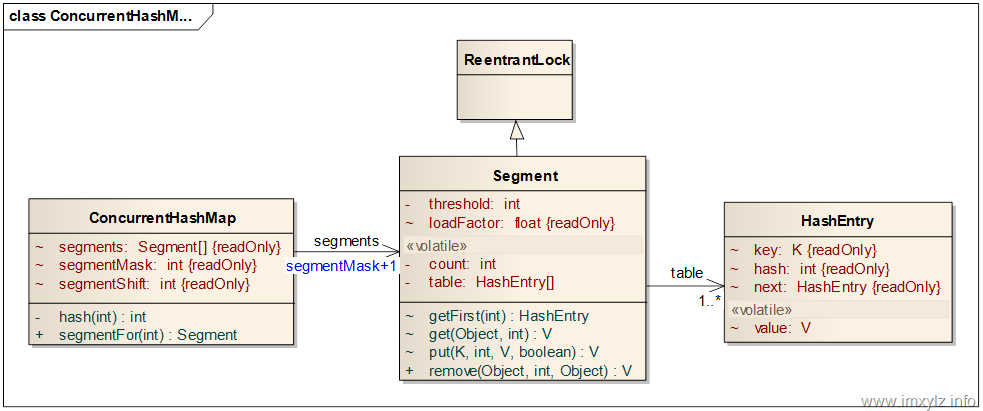
上圖就是ConcurrentHashMap的類圖。參考上面的說明和HashMap的原理分析，可以看到ConcurrentHashMap將整個(gè)對象列表分為segmentMask+1個(gè)片段（Segment）。其中每一個(gè)片段是一個(gè)類似于HashMap的結(jié)構(gòu)，它有一個(gè)HashEntry的數(shù)組，數(shù)組的每一項(xiàng)又是一個(gè)鏈表，通過HashEntry的next引用串聯(lián)起來。

這個(gè)類圖上面的數(shù)據(jù)結(jié)構(gòu)的定義非常有學(xué)問，接下來會(huì)一個(gè)個(gè)有針對性的分析。

首先如何從ConcurrentHashMap定位到HashEntry。在HashMap的原理分析部分說過，對于一個(gè)Hash的數(shù)據(jù)結(jié)構(gòu)來說，為了減少浪費(fèi)的空間和快速定位數(shù)據(jù)，那么就需要數(shù)據(jù)在Hash上的分布比較均勻。對于一次Map的查找來說，首先就需要定位到Segment，然后從過Segment定位到HashEntry鏈表，最后才是通過遍歷鏈表得到需要的元素。

在不討論并發(fā)的前提下先來討論如何定位到HashEntry的。在ConcurrentHashMap中是通過hash(key.hashCode())和segmentFor(hash)來得到Segment的。清單1 描述了如何定位Segment的過程。其中hash(int)是將key的hashCode進(jìn)行二次編碼，使之能夠在segmentMask+1個(gè)Segment上均勻分布（默認(rèn)是16個(gè)）。可以看到的是這里和HashMap還是有點(diǎn)不同的，這里采用的算法叫Wang/Jenkins hash，有興趣的可以參考資料1和參考資料2。總之它的目的就是使元素能夠均勻的分布在不同的Segment上，這樣才能夠支持最多segmentMask+1個(gè)并發(fā)，這里segmentMask+1是segments的大小。

清單1 定位Segment

private static int hash(int h) {
    // Spread bits to regularize both segment and index locations,
    // using variant of single-word Wang/Jenkins hash.
    h += (h <<  15) ^ 0xffffcd7d;
    h ^= (h >>> 10);
    h += (h <<   3);
    h ^= (h >>>  6);
    h += (h <<   2) + (h << 14);
    return h ^ (h >>> 16);
}
final Segment<K,V> segmentFor(int hash) {
    return segments[(hash >>> segmentShift) & segmentMask];
}

顯然在不能夠?qū)egment擴(kuò)容的情況下，segments的大小就應(yīng)該是固定的。所以在ConcurrentHashMap中segments/segmentMask/segmentShift都是常量，一旦初始化后就不能被再次修改，其中segmentShift是查找Segment的一個(gè)常量偏移量。

有了Segment以后再定位HashEntry就和HashMap中定位HashEntry一樣了，先將hash值與Segment中HashEntry的大小減1進(jìn)行與操作定位到HashEntry鏈表，然后遍歷鏈表就可以完成相應(yīng)的操作了。

能夠定位元素以后ConcurrentHashMap就已經(jīng)具有了HashMap的功能了，現(xiàn)在要解決的就是如何并發(fā)的問題。要解決并發(fā)問題，加鎖是必不可免的。再回頭看Segment的類圖，可以看到Segment除了有一個(gè)volatile類型的元素大小count外，Segment還是集成自ReentrantLock的。另外在前面的原子操作和鎖機(jī)制中介紹過，要想最大限度的支持并發(fā)，那么能夠利用的思路就是盡量讀操作不加鎖，寫操作不加鎖。如果是讀操作不加鎖，寫操作加鎖，對于競爭資源來說就需要定義為volatile類型的。volatile類型能夠保證happens-before法則，所以volatile能夠近似保證正確性的情況下最大程度的降低加鎖帶來的影響，同時(shí)還與寫操作的鎖不產(chǎn)生沖突。

同時(shí)為了防止在遍歷HashEntry的時(shí)候被破壞，那么對于HashEntry的數(shù)據(jù)結(jié)構(gòu)來說，除了value之外其他屬性就應(yīng)該是常量，否則不可避免的會(huì)得到ConcurrentModificationException。這就是為什么HashEntry數(shù)據(jù)結(jié)構(gòu)中key,hash,next是常量的原因(final類型）。

有了上面的分析和條件后再來看Segment的get/put/remove就容易多了。

get操作

清單2 Segment定位元素

V get(Object key, int hash) {
    if (count != 0) { // read-volatile
        HashEntry<K,V> e = getFirst(hash);
        while (e != null) {
            if (e.hash == hash && key.equals(e.key)) {
                V v = e.value;
                if (v != null)
                    return v;
                return readValueUnderLock(e); // recheck
            }
            e = e.next;
        }
    }
    return null;
}
HashEntry<K,V> getFirst(int hash) {
    HashEntry<K,V>[] tab = table;
    return tab[hash & (tab.length - 1)];
}

V readValueUnderLock(HashEntry<K,V> e) {
    lock();
    try {
        return e.value;
    } finally {
        unlock();
    }
}

清單2 描述的是Segment如何定位元素。首先判斷Segment的大小count>0，Segment的大小描述的是HashEntry不為空(key不為空)的個(gè)數(shù)。如果Segment中存在元素那么就通過getFirst定位到指定的HashEntry鏈表的頭節(jié)點(diǎn)上，然后遍歷此節(jié)點(diǎn)，一旦找到key對應(yīng)的元素后就返回其對應(yīng)的值。但是在清單2 中可以看到拿到HashEntry的value后還進(jìn)行了一次判斷操作，如果為空還需要加鎖再讀取一次（readValueUnderLock）。為什么會(huì)有這樣的操作？盡管ConcurrentHashMap不允許將value為null的值加入，但現(xiàn)在仍然能夠讀到一個(gè)為空的value就意味著此值對當(dāng)前線程還不可見（這是因?yàn)镠ashEntry還沒有完全構(gòu)造完成就賦值導(dǎo)致的，后面還會(huì)談到此機(jī)制）。

put操作

清單3 描述的是Segment的put操作。首先就需要加鎖了，修改一個(gè)競爭資源肯定是要加鎖的，這個(gè)毫無疑問。需要說明的是Segment集成的是ReentrantLock，所以這里加的鎖也就是獨(dú)占鎖，也就是說同一個(gè)Segment在同一時(shí)刻只有能一個(gè)put操作。

接下來來就是檢查是否需要擴(kuò)容，這和HashMap一樣，如果需要的話就擴(kuò)大一倍，同時(shí)進(jìn)行rehash操作。

查找元素就和get操作是一樣的，得到元素就直接修改其值就好了。這里onlyIfAbsent只是為了實(shí)現(xiàn)ConcurrentMap的putIfAbsent操作而已。需要說明以下幾點(diǎn)：

• 如果找到key對于的HashEntry后直接修改就好了，如果找不到那么就需要構(gòu)造一個(gè)新的HashEntry出來加到hash對于的HashEntry的頭部，同時(shí)就的頭部就加到新的頭部后面。這是因?yàn)镠ashEntry的next是final類型的，所以只能修改頭節(jié)點(diǎn)才能加元素加入鏈表中。
• 如果增加了新的操作后，就需要將count+1寫回去。前面說過count是volatile類型，而讀取操作沒有加鎖，所以只能把元素真正寫回Segment中的時(shí)候才能修改count值，這個(gè)要放到整個(gè)操作的最后。
• 在將新的HashEntry寫入table中時(shí)是通過構(gòu)造函數(shù)來設(shè)置value值的，這意味對table的賦值可能在設(shè)置value之前，也就是說得到了一個(gè)半構(gòu)造完的HashEntry。這就是重排序可能引起的問題。所以在讀取操作中，一旦讀到了一個(gè)value為空的value是就需要加鎖重新讀取一次。為什么要加鎖？加鎖意味著前一個(gè)寫操作的鎖釋放，也就是前一個(gè)鎖的數(shù)據(jù)已經(jīng)完成寫完了了，根據(jù)happens-before法則，前一個(gè)寫操作的結(jié)果對當(dāng)前讀線程就可見了。當(dāng)然在JDK 6.0以后不一定存在此問題。
• 在Segment中table變量是volatile類型，多次讀取volatile類型的開銷要不非volatile開銷要大，而且編譯器也無法優(yōu)化，所以在put操作中首先建立一個(gè)臨時(shí)變量tab指向table，多次讀寫tab的效率要比volatile類型的table要高，JVM也能夠?qū)Υ诉M(jìn)行優(yōu)化。

清單3 Segment的put操作

V put(K key, int hash, V value, boolean onlyIfAbsent) {
    lock();
    try {
        int c = count;
        if (c++ > threshold) // ensure capacity
            rehash();
        HashEntry<K,V>[] tab = table;
        int index = hash & (tab.length - 1);
        HashEntry<K,V> first = tab[index];
        HashEntry<K,V> e = first;
        while (e != null && (e.hash != hash || !key.equals(e.key)))
            e = e.next;

        V oldValue;
        if (e != null) {
            oldValue = e.value;
            if (!onlyIfAbsent)
                e.value = value;
        }
        else {
            oldValue = null;
            ++modCount;
            tab[index] = new HashEntry<K,V>(key, hash, first, value);
            count = c; // write-volatile
        }
        return oldValue;
    } finally {
        unlock();
    }
}

remove 操作

清單4 描述了Segment刪除一個(gè)元素的過程。同put一樣，remove也需要加鎖，這是因?yàn)閷able可能會(huì)有變更。由于HashEntry的next節(jié)點(diǎn)是final類型的，所以一旦刪除鏈表中間一個(gè)元素，就需要將刪除之前或者之后的元素重新加入新的鏈表。而Segment采用的是將刪除元素之前的元素一個(gè)個(gè)重新加入刪除之后的元素之前（也就是鏈表頭結(jié)點(diǎn)）來完成新鏈表的構(gòu)造。

清單4 Segment的remove操作

V remove(Object key, int hash, Object value) {
    lock();
    try {
        int c = count - 1;
        HashEntry<K,V>[] tab = table;
        int index = hash & (tab.length - 1);
        HashEntry<K,V> first = tab[index];
        HashEntry<K,V> e = first;
        while (e != null && (e.hash != hash || !key.equals(e.key)))
            e = e.next;

        V oldValue = null;
        if (e != null) {
            V v = e.value;
            if (value == null || value.equals(v)) {
                oldValue = v;
                // All entries following removed node can stay
                // in list, but all preceding ones need to be
                // cloned.
                ++modCount;
                HashEntry<K,V> newFirst = e.next;
                for (HashEntry<K,V> p = first; p != e; p = p.next)
                    newFirst = new HashEntry<K,V>(p.key, p.hash,
                                                  newFirst, p.value);
                tab[index] = newFirst;
                count = c; // write-volatile
            }
        }
        return oldValue;
    } finally {
        unlock();
    }
}

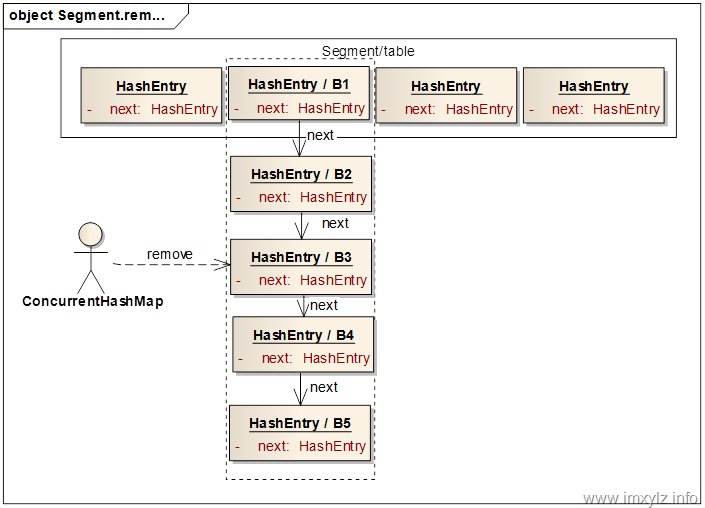
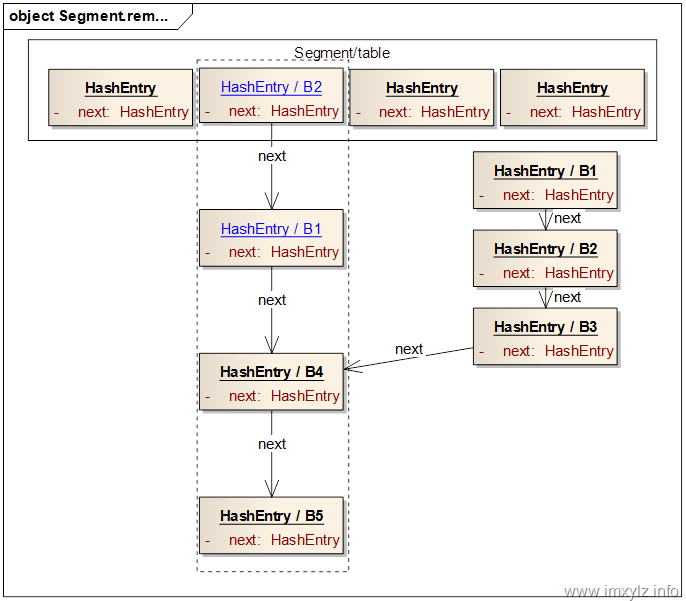
下面的示意圖描述了如何刪除一個(gè)已經(jīng)存在的元素的。假設(shè)我們要?jiǎng)h除B3元素。首先定位到B3所在的Segment，然后再定位到Segment的table中的B1元素，也就是Bx所在的鏈表。然后遍歷鏈表找到B3，找到之后就從頭結(jié)點(diǎn)B1開始構(gòu)建新的節(jié)點(diǎn)B1（藍(lán)色）加到B4的前面，繼續(xù)B1后面的節(jié)點(diǎn)B2構(gòu)造B2（藍(lán)色），加到由藍(lán)色的B1和B4構(gòu)成的新的鏈表。繼續(xù)下去，直到遇到B3后終止，這樣就構(gòu)造出來一個(gè)新的鏈表B2（藍(lán)色）->B1（藍(lán)色）->B4->B5，然后將此鏈表的頭結(jié)點(diǎn)B2（藍(lán)色）設(shè)置到Segment的table中。這樣就完成了元素B3的刪除操作。需要說明的是，盡管就的鏈表仍然存在(B1->B2->B3->B4->B5)，但是由于沒有引用指向此鏈表，所以此鏈表中無引用的（B1->B2->B3）最終會(huì)被GC回收掉。這樣做的一個(gè)好處是，如果某個(gè)讀操作在刪除時(shí)已經(jīng)定位到了舊的鏈表上，那么此操作仍然將能讀到數(shù)據(jù)，只不過讀取到的是舊數(shù)據(jù)而已，這在多線程里面是沒有問題的。

除了對單個(gè)元素操作外，還有對全部的Segment的操作，比如size()操作等。

size操作

size操作涉及到統(tǒng)計(jì)所有Segment的大小，這樣就會(huì)遍歷所有的Segment，如果每次加鎖就會(huì)導(dǎo)致整個(gè)Map都被鎖住了，任何需要鎖的操作都將無法進(jìn)行。這里用到了一個(gè)比較巧妙的方案解決此問題。

在Segment中有一個(gè)變量modCount，用來記錄Segment結(jié)構(gòu)變更的次數(shù)，結(jié)構(gòu)變更包括增加元素和刪除元素，每增加一個(gè)元素操作就+1，每進(jìn)行一次刪除操作+1，每進(jìn)行一次清空操作(clear)就+1。也就是說每次涉及到元素個(gè)數(shù)變更的操作modCount都會(huì)+1，而且一直是增大的，不會(huì)減小。

遍歷兩次ConcurrentHashMap中的segments，每次遍歷是記錄每一個(gè)Segment的modCount，比較兩次遍歷的modCount值的和是否相同，如果相同就返回在遍歷過程中獲取的Segment的count的和，也就是所有元素的個(gè)數(shù)。如果不相同就重復(fù)再做一次。重復(fù)一次還不相同就將所有Segment鎖住，一個(gè)一個(gè)的獲取其大小(count)，最后將這些count加起來得到總的大小。當(dāng)然了最后需要將鎖一一釋放。清單5 描述了這個(gè)過程。

這里有一個(gè)比較高級的話題是為什么在讀取modCount的時(shí)候總是先要讀取count一下。為什么不是先讀取modCount然后再讀取count的呢？也就是說下面的兩條語句能否交換下順序？

sum += segments[i].count;

mcsum += mc[i] = segments[i].modCount;

答案是不能！為什么？這是因?yàn)閙odCount總是在加鎖的情況下才發(fā)生變化，所以不會(huì)發(fā)生多線程同時(shí)修改的情況，也就是沒必要時(shí)volatile類型。另外總是在count修改的情況下修改modCount，而count是一個(gè)volatile變量。于是這里就充分利用了volatile的特性。

根據(jù)happens-before法則，第（3）條：對volatile字段的寫入操作happens-before于每一個(gè)后續(xù)的同一個(gè)字段的讀操作。也就是說一個(gè)操作C在volatile字段的寫操作之后，那么volatile寫操作之前的所有操作都對此操作C可見。所以修改modCount總是在修改count之前，也就是說如果讀取到了一個(gè)count的值，那么在count變化之前的modCount也就能夠讀取到，換句話說就是如果看到了count值的變化，那么就一定看到了modCount值的變化。而如果上面兩條語句交換下順序就無法保證這個(gè)結(jié)果一定存在了。

在ConcurrentHashMap.containsValue中，可以看到每次遍歷segments時(shí)都會(huì)執(zhí)行int c = segments[i].count;，但是接下來的語句中又不用此變量c，盡管如此JVM仍然不能將此語句優(yōu)化掉，因?yàn)檫@是一個(gè)volatile字段的讀取操作，它保證了一些列操作的happens-before順序，所以是至關(guān)重要的。在這里可以看到：

ConcurrentHashMap將volatile發(fā)揮到了極致！

另外isEmpty操作于size操作類似，不再累述。

清單5 ConcurrentHashMap的size操作

public int size() {
    final Segment<K,V>[] segments = this.segments;
    long sum = 0;
    long check = 0;
    int[] mc = new int[segments.length];
    // Try a few times to get accurate count. On failure due to
    // continuous async changes in table, resort to locking.
    for (int k = 0; k < RETRIES_BEFORE_LOCK; ++k) {
        check = 0;
        sum = 0;
        int mcsum = 0;
        for (int i = 0; i < segments.length; ++i) {
            sum += segments[i].count;
            mcsum += mc[i] = segments[i].modCount;
        }
        if (mcsum != 0) {
            for (int i = 0; i < segments.length; ++i) {
                check += segments[i].count;
                if (mc[i] != segments[i].modCount) {
                    check = -1; // force retry
                    break;
                }
            }
        }
        if (check == sum)
            break;
    }
    if (check != sum) { // Resort to locking all segments
        sum = 0;
        for (int i = 0; i < segments.length; ++i)
            segments[i].lock();
        for (int i = 0; i < segments.length; ++i)
            sum += segments[i].count;
        for (int i = 0; i < segments.length; ++i)
            segments[i].unlock();
    }
    if (sum > Integer.MAX_VALUE)
        return Integer.MAX_VALUE;
    else
        return (int)sum;
}

ConcurrentSkipListMap/Set

本來打算介紹下ConcurrentSkipListMap的，結(jié)果打開源碼一看，徹底放棄了。那里面的數(shù)據(jù)結(jié)構(gòu)和算法我估計(jì)研究一周也未必能夠完全弄懂。很久以前我看TreeMap的時(shí)候就頭大，想想那些復(fù)雜的“紅黑二叉樹”我頭都大了。這些都?xì)w咎于從前沒有好好學(xué)習(xí)《數(shù)據(jù)結(jié)構(gòu)和算法》，現(xiàn)在再回頭看這些復(fù)雜的算法感覺非常頭疼，為了減少腦細(xì)胞的死亡，暫且還是不要惹這些“玩意兒”。有興趣的可以看看參考資料4 中對TreeMap的介紹。

參考資料：

1. Hash this
2. Single-word Wang/Jenkins Hash in ConcurrentHashMap
3. 指令重排序與happens-before法則
4. 通過分析 JDK 源代碼研究 TreeMap 紅黑樹算法實(shí)現(xiàn)