在一個n乘n的棋盤上有一匹馬���,要求這匹馬不重復的把每個格子都跳一邊���。這里馬的走法和中國象棋里的馬一樣��。如下圖所示,一步只能跳到位于棋盤內的1到8的八個格子里�����。
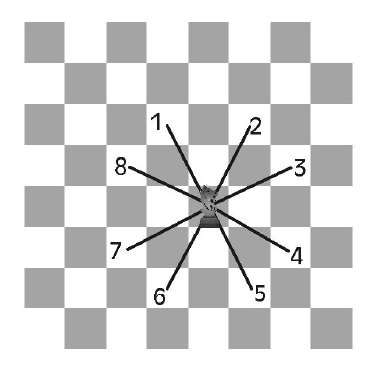
對這道題目��,一個最直觀的解法就是使用所謂的Backtracking的思路��,從起點開始���,一直跳��,沒格子可跳了,就退回一步�����,接著往下跳�����。在這個過程中,記下所有跳過的格子�����,不重復跳到跳過的格子里���。直到所有的格子都跳完為止���,也就是發現一個解法���,或者所有可能的跳法都試過��,還沒有找到一個跳法���,也就是沒有解法���。
很簡單的思路��,但是如果你不熟悉Recursion的編程的話,要實現卻不那么簡單。Recursion是計算機科學中最重要的一個概念和工具,也是計算機科學強大動力的源泉�����,怎么強調都不過分�����。Recursion在計算機的各個學科都有著非常重要的作用�����。所有可計算的函數可以歸結在Partial Recursive Function下��。掌握和熟悉Recursion的思路可以說是您步入計算機科學殿堂的第一步�����。
下面是我用Java編寫的跳馬題的Recursive的解法
1 private static int[][] board;
2 private static int length;
3
4 /**
5 * search a solution of Springerproblem
6 *
7 * @param n board of n*n fields
8 * @param x [1 .. n] horizontal coordinate
9 * @param y [1 .. n] vertical coordinate
10 * @return true found, false no
11 */
12 public static boolean search(int n, int x, int y) {
13 if (n < 1 || x < 1 || x > n || y < 1 || y > n) {
14 System.out.println("wrong input dimension.");
15 return false;
16 }
17
18 board = new int[n + 1][n + 1];
19 length = n;
20 for (int i = 1; i <= length; i++)
21 for (int j = 1; j < length; j++)
22 board[i][j] = 0;
23
24 return research(x, y, 1);
25 }
26
27 /**
28 * recursive search
29 *
30 * @param x 起點x
31 * @param y 起點y
32 * @param step 第幾步
33 * @return true 找到解法,false��,失敗了
34 */
35 private static boolean research(int x, int y, int step) {
36 if (x < 1 || x > length || y < 1 || y > length)
37 return false;
38 if (board[x][y] > 0)
39 return false;
40
41 board[x][y] = step;
42 if (step == length * length)
43 return true;
44
45 if (research(x - 1, y - 2, step + 1))
46 return true;
47 if (research(x - 1, y + 2, step + 1))
48 return true;
49 if (research(x + 1, y - 2, step + 1))
50 return true;
51 if (research(x + 1, y + 2, step + 1))
52 return true;
53 if (research(x - 2, y - 1, step + 1))
54 return true;
55 if (research(x - 2, y + 1, step + 1))
56 return true;
57 if (research(x + 2, y - 1, step + 1))
58 return true;
59 if (research(x + 2, y + 1, step + 1))
60 return true;
61
62 board[x][y] = 0;
63 return false;
64 }
初學Recursion的時候���,很不習慣他的思維方式���。有時候甚至會奇怪這樣就把問題解決了��。在使用Recursion編程的時候�����,可以假定您已經有一個要找的函數f了,然后應用f 較小的情況來解決大的情況,最小的情況另外特殊求解���。這個過程中最關鍵的就是設計f的接口和功能,在解題的過程中,您可能要不斷的調整f的接口和功能��。
轉載請保留
http://www.tkk7.com/xilaile/archive/2007/04/06/109001.html