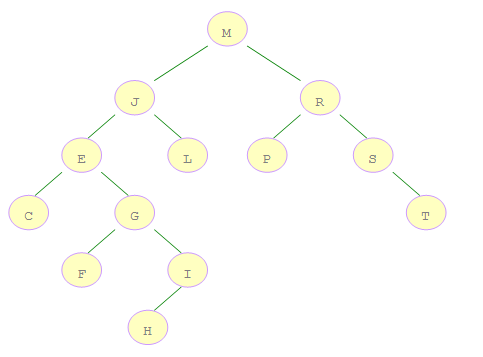
二叉排序樹 ( Binary Sort Tree ) 又稱 二叉查找樹 ( Binary Search Tree )����。
它或者是一棵空樹,或者是具有下列性質的二叉樹:
1. 若它的左子樹不空����,則左子樹上所有結點的值均小于它的根結點的值
2. 若它的右子樹不空�����,則右子樹上所有結點的值均大于它的根結點的值
3. 它的左、右子樹也分別為二叉排序樹
二叉排序樹的查找算法
在二叉排序樹 T 中查找 V 的過程為:
1. 若 T 是空樹����,則搜索失敗
2. 若 V 等于 T 的根節點的數據域之值�����,則查找成功
3. 若 V 小于 T 的根節點的數據域之值,則搜索 T 的左子樹,否則查找 T 的右子樹
二叉排序樹查找算法代碼片段
//查找結點
//如果找不到,see 指向最后一個結點,并返回false; 如果找到,see 指向該結點,并返回true
bool search(Tree root, TNode parent, TNode &see, Element key){
if(!root){
see = parent;
return false;
}
if(root->data == key){
see = root;
return true;
}
if(root->data > key){
return search(root->lchild, root, see, key);
}else{
return search(root->rchild, root, see, key);
}
}
//重載函數
//如果找不到,則返回NULL; 如果找到,則返回該結點
TNode search(Tree root, TNode parent, Element key){
if(!root){
return NULL;
}
if(root->data == key){
return root;
}
if(root->data > key){
return search(root->lchild, root, key);
}else{
return search(root->rchild, root, key);
}
}
//重載函數
TNode search(Tree root, Element e){
return search(root, NULL, e);
}
二叉排序樹插入結點的算法
向一個二叉查找樹 T 中插入一個結點 S 的過程為:
1. 若 T 是空樹��,則將 S 所指結點作為根結點插入
2. 若 S 的數據域的值等于 T 的根結點的數據域之值����,說明該結點已經存在��,不進行插入操作
3. 若 S 的數據域的值小于 T 的根結點的數據域之值��,則把 S 所指結點插入到左子樹中,否則插入到右子樹中
二叉排序樹插入結點的算法代碼片段
//二叉排序樹插入結點
bool insertNode(Tree &root, Element e){
TNode parent;
bool isFound = search(root, NULL, parent, e); //查找該結點
if(isFound){ //已經存在
printf("該結點已經存在,插入操作失敗!");
return false;
}
TNode node = (TNode)malloc(sizeof(Node));
node->data = e;
node->lchild = node->rchild = NULL;
if(!parent){ //空樹
root = node;
}else{
if(parent->data > e){
parent->lchild = node;
}else{
parent->rchild = node;
}
}
return true;
}
二叉排序樹刪除結點的算法
分三種情況討論:
1. 若 *current 結點為葉子結點�����,即PL(左子樹)和PR(右子樹)均為空樹。由于刪去葉子結點不破壞整棵樹的結構����,則只需修改其雙親結點的指針即可
2. 若 *current 結點只有左子樹PL或右子樹PR�����,此時只要令PL或PR直接成為其雙親結點 *cparent 的左子樹(當 *current 是左子樹)
或右子樹(當 *current 是右子樹)即可,作此修改也不破壞二叉排序樹的特性
3. 若 *current 結點的左子樹和右子樹均不空��。在刪去 *current 之后�����,為保持其它元素之間的相對位置不變��,可按中序遍歷保持有序進行調整,
可以有兩種做法:
其一是令 *current 的左子樹為 *cparent 的左/右(依 *current 是 *cparent 的左子樹還是右子樹而定)子樹,
*precursor 為 *current 左子樹的最右下的結點,而 *current 的右子樹為 *precursor 的右子樹
其二是令 *current 的直接前驅(或直接后繼)替代 *current ,然后再從二叉排序樹中刪去它的直接前驅(或直接后繼)
二叉排序樹刪除結點的算法代碼片段
//刪除二叉排序樹結點
void deleteNode(Tree &root, Element key){
Node *current, *cparent, *del;
current = root; //當前結點
cparent = NULL; //當前結點的雙親結點
del = NULL; //刪除的結點
while(current && current->data != key){ //查找被刪除的結點,可直接調用上面的search函數
cparent = current;
if(current->data > key){
current = current->lchild;
}else{
current = current->rchild;
}
}
if(!current){ //沒找到
printf("刪除的結點不存在!");
return ;
}
del = current; //找到了
if(!current->lchild){ //被刪結點無左子樹,重接右子樹
if(current == cparent->lchild)
cparent->lchild = current->rchild;
else
cparent->rchild = current->rchild;
}else if(!current->rchild){ //被刪結點無右子樹,重接左子樹
if(current == cparent->lchild)
cparent->lchild = current->lchild;
else
cparent->rchild = current->lchild;
}else{ //被刪結點同時存在左子樹和右子樹
Node *precursor, *parent;
precursor = current->lchild; //被刪結點的直接前驅結點
parent = current; //前驅結點的雙親結點
while(precursor->rchild){ //查找前驅結點(中序遍歷到最后)
parent = precursor;
precursor = precursor->rchild;
}
current->data = precursor->data; //前驅結點替換被刪結點
if(parent != current){ //重接右子樹
parent->rchild = precursor->lchild;
}else{ //重接左子樹
parent->lchild = precursor->lchild;
}
del = precursor;
}
free(del); //釋放被刪結點內存空間
}
完整代碼:
/**
* <!--
* File : binarysorttree.h
* Author : fancy
* Email : fancydeepin@yeah.net
* Date : 2013-02-04
* --!>
*/
#include <stdio.h>
#include <stdlib.h>
#include <malloc.h>
#define Element char
#define format "%c"
typedef struct Node {
Element data;
struct Node *lchild;
struct Node *rchild;
} *Tree, *TNode;
int index = 0; //全局索引變量
//二叉樹構造器,按先序遍歷順序構造二叉樹
//無左子樹或右子樹用'#'表示
void treeNodeConstructor(Tree &root, Element data[]){
Element e = data[index++];
if(e == '#'){
root = NULL;
}else{
root = (Node *)malloc(sizeof(Node));
root->data = e;
treeNodeConstructor(root->lchild, data);
treeNodeConstructor(root->rchild, data);
}
}
//查找結點
//如果找不到,see 指向最后一個結點,并返回false; 如果找到,see 指向該結點,并返回true
bool search(Tree root, TNode parent, TNode &see, Element key){
if(!root){
see = parent;
return false;
}
if(root->data == key){
see = root;
return true;
}
if(root->data > key){
return search(root->lchild, root, see, key);
}else{
return search(root->rchild, root, see, key);
}
}
//重載函數
//如果找不到,則返回NULL; 如果找到,則返回該結點
TNode search(Tree root, TNode parent, Element key){
if(!root){
return NULL;
}
if(root->data == key){
return root;
}
if(root->data > key){
return search(root->lchild, root, key);
}else{
return search(root->rchild, root, key);
}
}
//重載函數
TNode search(Tree root, Element e){
return search(root, NULL, e);
}
//刪除二叉排序樹結點
void deleteNode(Tree &root, Element key){
Node *current, *cparent, *del;
current = root; //當前結點
cparent = NULL; //當前結點的雙親結點
del = NULL; //刪除的結點
while(current && current->data != key){ //查找被刪除的結點,可直接調用上面的search函數
cparent = current;
if(current->data > key){
current = current->lchild;
}else{
current = current->rchild;
}
}
if(!current){ //沒找到
printf("刪除的結點不存在!");
return ;
}
del = current; //找到了
if(!current->lchild){ //被刪結點無左子樹,重接右子樹
if(current == cparent->lchild)
cparent->lchild = current->rchild;
else
cparent->rchild = current->rchild;
}else if(!current->rchild){ //被刪結點無右子樹,重接左子樹
if(current == cparent->lchild)
cparent->lchild = current->lchild;
else
cparent->rchild = current->lchild;
}else{ //被刪結點同時存在左子樹和右子樹
Node *precursor, *parent;
precursor = current->lchild; //被刪結點的直接前驅結點
parent = current; //前驅結點的雙親結點
while(precursor->rchild){ //查找前驅結點(中序遍歷到最后)
parent = precursor;
precursor = precursor->rchild;
}
current->data = precursor->data; //前驅結點替換被刪結點
if(parent != current){ //重接右子樹
parent->rchild = precursor->lchild;
}else{ //重接左子樹
parent->lchild = precursor->lchild;
}
del = precursor;
}
free(del); //釋放被刪結點內存空間
}
//二叉排序樹插入結點
bool insertNode(Tree &root, Element e){
TNode parent;
bool isFound = search(root, NULL, parent, e); //查找該結點
if(isFound){ //已經存在
printf("該結點已經存在,插入操作失敗!");
return false;
}
TNode node = (TNode)malloc(sizeof(Node));
node->data = e;
node->lchild = node->rchild = NULL;
if(!parent){ //空樹
root = node;
}else{
if(parent->data > e){
parent->lchild = node;
}else{
parent->rchild = node;
}
}
return true;
}
//先序遍歷
void preorderTraversal(Tree root){
if(root){
printf(format, root->data);
preorderTraversal(root->lchild);
preorderTraversal(root->rchild);
}
}
//中序遍歷二叉樹
void inorderTraversal(Tree root){
if(root){
inorderTraversal(root->lchild);
printf(format, root->data);
inorderTraversal(root->rchild);
}
}
//后序遍歷二叉樹
void postorderTraversal(Tree root){
if(root){
postorderTraversal(root->lchild);
postorderTraversal(root->rchild);
printf(format, root->data);
}
}
/**
* <!--
* File : BinarySortTree.cpp
* Author : fancy
* Email : fancydeepin@yeah.net
* Date : 2013-02-04
* --!>
*/
#include "binarysorttree.h"
int main() {
//上圖所示的二叉樹先序遍歷序列,其中用'#'表示結點無左子樹或無右子樹
Element data[27] = {'M', 'J', 'E', 'C', '#', '#', 'G', 'F', '#', '#', 'I', 'H',
'#','#', '#', 'L', '#', '#', 'R', 'P', '#', '#', 'S', '#', 'T', '#', '#'};
Tree tree;
treeNodeConstructor(tree, data);
printf("先序遍歷結果: ");
preorderTraversal(tree);
printf("\n");
//TEST 搜索
TNode node = search(tree, 'F');
if(node){
printf("Found it : %c\n", node->data);
}else{
printf("NOT FOUND\n");
}
//TEST 插入結點
insertNode(tree, 'K');
printf("插入K結點后,先序遍歷結果: ");
preorderTraversal(tree);
printf("\n");
//TEST 刪除無左右子樹的結點
deleteNode(tree, 'P');
printf("刪除P結點后,先序遍歷結果: ");
preorderTraversal(tree);
printf("\n");
//TEST 刪除無左子樹的結點
deleteNode(tree, 'S');
printf("刪除S結點后,先序遍歷結果: ");
preorderTraversal(tree);
printf("\n");
//TEST 刪除無右子樹的結點
deleteNode(tree, 'I');
printf("刪除I結點后,先序遍歷結果: ");
preorderTraversal(tree);
printf("\n");
//TEST 刪除有左右子樹的結點
deleteNode(tree, 'J');
printf("刪除J結點后,先序遍歷結果: ");
preorderTraversal(tree);
printf("\n");
/**
* 控制臺輸出結果:
*
* 先序遍歷結果: MJECGFIHLRPST
* Found it : F
* 插入K結點后,先序遍歷結果: MJECGFIHLKRPST
* 刪除P結點后,先序遍歷結果: MJECGFIHLKRST
* 刪除S結點后,先序遍歷結果: MJECGFIHLKRT
* 刪除I結點后,先序遍歷結果: MJECGFHLKRT
* 刪除J結點后,先序遍歷結果: MHECGFLKRT
*/
return 0;
}
posted on 2013-02-04 10:21
fancydeepin 閱讀(1839)
評論(0) 編輯 收藏