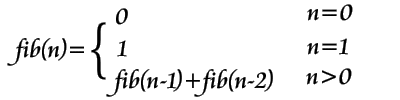這兩天翻了下 Kent? Beck 的 Test-Driven Development By Example 感覺還不錯,第一部分的例子講的挺好,本來想歸納一下,貌似太長了,等有時間了再歸納下,最后看到了附錄里面的一個Fibonacci數(shù)列的例子感覺也有那么點TDD的味道在里面,總結(jié)分享一下:
讓我們從最簡單的fibonacci(0)=0開始吧,先寫測試如下:
 import
?junit.framework.TestCase;????????
import
?junit.framework.TestCase;????????
 ???????
???????

 public
?
class
?TestFibonacci?
extends
?TestCase?
public
?
class
?TestFibonacci?
extends
?TestCase?
 {????????
{????????

 ????
public
?
void
?testFibonacci()
????
public
?
void
?testFibonacci()
 {????????
{????????
 ????????assertEquals(
0
,fibonacci(
0
));????????
????????assertEquals(
0
,fibonacci(
0
));????????
 ????}
????????????
????}
????????????
 }
?????
}
?????
添加fibonacci方法的簡單實現(xiàn)即可:

 private
?
int
?fibonacci(
int
?i)?
private
?
int
?fibonacci(
int
?i)?
 {??????????????
{??????????????
 ????????
return
?
0
;????????
????????
return
?
0
;????????
 ????}
??
????}
??
很顯然順利通過了測試;
再加一個測試實現(xiàn)fibonacci(1)=1;如下:
 import
?junit.framework.TestCase;????????
import
?junit.framework.TestCase;????????
 ???????
???????

 public
?
class
?TestFibonacci?
extends
?TestCase?
public
?
class
?TestFibonacci?
extends
?TestCase?
 {????????
{????????

 ????
public
?
void
?testFibonacci()
????
public
?
void
?testFibonacci()
 {????????
{????????
 ????????assertEquals(
0
,fibonacci(
0
));????????
????????assertEquals(
0
,fibonacci(
0
));????????
 ????????assertEquals(
1
,fibonacci(
1
));????????
????????assertEquals(
1
,fibonacci(
1
));????????
 ????}
????????????
????}
????????????
 }
???????
}
???????

為了順利通過測試,只需簡單的改動下fibonacci方法實現(xiàn)即可;

 private
?
int
?fibonacci(
int
?i)?
private
?
int
?fibonacci(
int
?i)?
 {??????????????
{??????????????
 ????????
if
(i
==
0
)?
return
?
0
;????????
????????
if
(i
==
0
)?
return
?
0
;????????
 ????????
else
?
return
?
1
;????????
????????
else
?
return
?
1
;????????
 ????}
???
????}
???
在添加第三個測試條件fibonacci(2)=1時候發(fā)現(xiàn),隨著測試條件的增多無疑帶來了大量的斷言重復(fù)代碼,通過分析我們可以將testFibonacci方法改寫如下:

 public
?
void
?testFibonacci()
public
?
void
?testFibonacci()
 {????
{????

 ????????
int
?cases[][]
=
????????
int
?cases[][]
=
 {
{
 {
0
,
0
}
,
{
0
,
0
}
,
 {
1
,
1
}
}
;????
{
1
,
1
}
}
;????
 ????????
for
(
int
?i
=
0
;i?
????????
for
(
int
?i
=
0
;i?
 ????????????assertEquals(cases[i][
1
],fibonacci(cases[i][
0
]));???????
????????????assertEquals(cases[i][
1
],fibonacci(cases[i][
0
]));???????
 ????}
???
????}
???

這樣我們就可以很容易的添加測試條件:fibonacci(2)=1;
 import
?junit.framework.TestCase;????
import
?junit.framework.TestCase;????
 ???
???

 public
?
class
?TestFibonacci?
extends
?TestCase?
public
?
class
?TestFibonacci?
extends
?TestCase?
 {????
{????

 ????
public
?
void
?testFibonacci()
????
public
?
void
?testFibonacci()
 {????
{????

 ????????
int
?cases[][]
=
????????
int
?cases[][]
=
 {
{
 {
0
,
0
}
,
{
0
,
0
}
,
 {
1
,
1
}
,
{
1
,
1
}
,
 {
2
,
1
}
}
;????
{
2
,
1
}
}
;????
 ????????
for
(
int
?i
=
0
;i?
????????
for
(
int
?i
=
0
;i?
 ????????????assertEquals(cases[i][
1
],fibonacci(cases[i][
0
]));???????
????????????assertEquals(cases[i][
1
],fibonacci(cases[i][
0
]));???????
 ????}
????
????}
????
 ???
???

 ????
private
?
int
?fibonacci(
int
?i)?
????
private
?
int
?fibonacci(
int
?i)?
 {??????????
{??????????
 ????????
if
(i
==
0
)?
return
?
0
;????
????????
if
(i
==
0
)?
return
?
0
;????
 ????????
else
?
return
?
1
;????
????????
else
?
return
?
1
;????
 ????}
????
????}
????
 }
???
}
???

嘿嘿,很順利,狀態(tài)條依然出現(xiàn)的是綠色,那我們就不管代碼到底合不合理了,出現(xiàn)綠色就是王道,繼續(xù)添加下一個測試條件:fibonacci(3)=2;
 import
?junit.framework.TestCase;????
import
?junit.framework.TestCase;????
 ???
???

 public
?
class
?TestFibonacci?
extends
?TestCase?
public
?
class
?TestFibonacci?
extends
?TestCase?
 {????
{????

 ????
public
?
void
?testFibonacci()
????
public
?
void
?testFibonacci()
 {????
{????

 ????????
int
?cases[][]
=
????????
int
?cases[][]
=
 {
{
 {
0
,
0
}
,
{
0
,
0
}
,
 {
1
,
1
}
,
{
1
,
1
}
,
 {
2
,
1
}
,
{
2
,
1
}
,
 {
3
,
2
}
}
;????
{
3
,
2
}
}
;????
 ????????
for
(
int
?i
=
0
;i?
????????
for
(
int
?i
=
0
;i?
 ????????????assertEquals(cases[i][
1
],fibonacci(cases[i][
0
]));???????
????????????assertEquals(cases[i][
1
],fibonacci(cases[i][
0
]));???????
 ????}
????
????}
????
 ???
???

 ????
private
?
int
?fibonacci(
int
?i)?
????
private
?
int
?fibonacci(
int
?i)?
 {??????????
{??????????
 ????????
if
(i
==
0
)?
return
?
0
;????
????????
if
(i
==
0
)?
return
?
0
;????
 ????????
else
?
return
?
1
;????
????????
else
?
return
?
1
;????
 ????}
????
????}
????
 }
???
}
???

終于又出現(xiàn)紅色了,it fails .說明我們又將快有新進展了.為了滿足fibonacci(3)=2,也很簡單,簡單的修改下fibonacci方法即可,如下:

 private?int?fibonacci(int?i)?
private?int?fibonacci(int?i)? {??????????
{??????????
 ????????if(i==0)?return?0;????
????????if(i==0)?return?0;????
 ????????if(i<=2)?return?1;????
????????if(i<=2)?return?1;????
 ????????else?return?2;????
????????else?return?2;????
 ????}??
????}??又出現(xiàn)綠色了吧! 這里返回的2可以表示為1+1;
我們可以寫成:

 private?int?fibonacci(int?i)?
private?int?fibonacci(int?i)? {??????????
{??????????
 ????????if(i==0)?return?0;????
????????if(i==0)?return?0;????
 ????????if(i<=2)?return?1;????
????????if(i<=2)?return?1;????
 ????????else?return?fibonacci(i-1)+1;????
????????else?return?fibonacci(i-1)+1;????
 ????}???
????}???

第二個1可以寫成fibonacci(i-2):
 import?junit.framework.TestCase;????
import?junit.framework.TestCase;????
 ???
???

 public?class?TestFibonacci?extends?TestCase?
public?class?TestFibonacci?extends?TestCase? {????
{????

 ????public?void?testFibonacci()
????public?void?testFibonacci() {????
{????

 ????????int?cases[][]=
????????int?cases[][]= {
{ {0,0},
{0,0}, {1,1},
{1,1}, {2,1},
{2,1}, {3,2}};????
{3,2}};????
 ????????for(int?i=0;i?
????????for(int?i=0;i?
 ????????????assertEquals(cases[i][1],fibonacci(cases[i][0]));???????
????????????assertEquals(cases[i][1],fibonacci(cases[i][0]));???????
 ????}????
????}????
 ???
???

 ????private?int?fibonacci(int?i)?
????private?int?fibonacci(int?i)? {??????????
{??????????
 ????????if(i==0)?return?0;????
????????if(i==0)?return?0;????
 ????????if(i==1)?return?1;????
????????if(i==1)?return?1;????
 ????????else?return?fibonacci(i-1)+fibonacci(i-2);????
????????else?return?fibonacci(i-1)+fibonacci(i-2);????
 ????}????
????}????
 }???
}???

再添加測試條件:fibonacci(4)=3;fibonacci(5)=5:
 import?junit.framework.TestCase;????
import?junit.framework.TestCase;????
 ???
???

 public?class?TestFibonacci?extends?TestCase?
public?class?TestFibonacci?extends?TestCase? {????
{????

 ????public?void?testFibonacci()
????public?void?testFibonacci() {????
{????

 ????????int?cases[][]=
????????int?cases[][]= {
{ {0,0},
{0,0}, {1,1},
{1,1}, {2,1},
{2,1}, {3,2},
{3,2}, {4,3},
{4,3}, {5,5}};????
{5,5}};????
 ????????for(int?i=0;i?
????????for(int?i=0;i?
 ????????????assertEquals(cases[i][1],fibonacci(cases[i][0]));???????
????????????assertEquals(cases[i][1],fibonacci(cases[i][0]));???????
 ????}????
????}????
 ???
???

 ????private?int?fibonacci(int?i)?
????private?int?fibonacci(int?i)? {??????????
{??????????
 ????????if(i==0)?return?0;????
????????if(i==0)?return?0;????
 ????????if(i==1)?return?1;????
????????if(i==1)?return?1;????
 ????????else?return?fibonacci(i-1)+fibonacci(i-2);????
????????else?return?fibonacci(i-1)+fibonacci(i-2);????
 ????}????
????}????
 }?
}?依然是綠色,呵呵,我們得到了正確的Fibonacci數(shù)列,驅(qū)動源于測試.
附:
Fibonacci數(shù)列簡介:Fibonacci數(shù)列從第0項開始依次為0,1,1,2,3,5,8……的數(shù)列,它存在如下特點:第0,1個數(shù)為0,1。從第2個數(shù)開始,該數(shù)是前面兩個數(shù)之和。即該數(shù)列第n項的值滿足如下公式: