canonical

作者： Canonical

眾所周知，計算機科學得以存在的基石是兩個基本理論：圖靈于1936年提出的圖靈機理論和丘奇同年早期發表的Lambda演算理論。這兩個理論奠定了所謂通用計算（Universal Computation）的概念基礎，描繪了具有相同計算能力（圖靈完備），但形式上卻南轅北轍、大相徑庭的兩條技術路線。如果把這兩種理論看作是上帝所展示的世界本源面貌的兩個極端，那么是否存在一條更加中庸靈活的到達通用計算彼岸的中間路徑?

自1936年以來，軟件作為計算機科學的核心應用，一直處在不間斷的概念變革過程中，各類程序語言/系統架構/設計模式/方法論層出不窮，但是究其軟件構造的基本原理，仍然沒有脫出兩個基本理論最初所設定的范圍。如果定義一種新的軟件構造理論，它所引入的新概念本質上能有什么特異之處？能夠解決什么棘手的問題？

本文中筆者提出在圖靈機和lambda演算的基礎上可以很自然的引入一個新的核心概念--可逆性，從而形成一個新的軟件構造理論--可逆計算（Reversible Computation）。可逆計算提供了區別于目前業內主流方法的更高層次的抽象手段，可以大幅降低軟件內在的復雜性，為粗粒度軟件復用掃除了理論障礙。

可逆計算的思想來源不是計算機科學本身，而是理論物理學，它將軟件看作是處于不斷演化過程中的抽象實體， 在不同的復雜性層次上由不同的運算規則所描述，它所關注的是演化過程中產生的微小差量如何在系統內有序的傳播并發生相互作用。

本文第一節將介紹可逆計算理論的基本原理與核心公式，第二節分析可逆計算理論與組件和模型驅動等傳統軟件構造理論的區別和聯系，并介紹可逆計算理論在軟件復用領域的應用，第三節從可逆計算角度解構Docker、React等創新技術實踐。

一. 可逆計算的基本原理

可逆計算可以看作是在真實的信息有限的世界中，應用圖靈計算和lambda演算對世界建模的一種必然結果，我們可以通過以下簡單的物理圖像來理解這一點。

首先，圖靈機是一種結構固化的機器，它具有可枚舉的有限的狀態集合，只能執行有限的幾條操作指令，但是可以從無限長的紙帶上讀取和保存數據。例如我們日常使用的電腦，它在出廠的時候硬件功能就已經確定了，但是通過安裝不同的軟件，傳入不同的數據文件，最終它可以自動產生任意復雜的目標輸出。圖靈機的計算過程在形式上可以寫成

與圖靈機相反的是，lambda演算的核心概念是函數，一個函數就是一臺小型的計算機器，函數的復合仍然是函數，也就是說可以通過機器和機器的遞歸組合來產生更加復雜的機器。lambda演算的計算能力與圖靈機等價，這意味著如果允許我們不斷創建更加復雜的機器，即使輸入一個常數0，我們也可以得到任意復雜的目標輸出。lambda演算的計算過程在形式上可以寫成

可以看出，以上兩種計算過程都可以被表達為Y=F(X) 這樣一種抽象的形式。如果我們把Y=F(X)理解為一種建模過程，即我們試圖理解輸入的結構以及輸入和輸出之間的映射關系，采用最經濟的方式重建輸出，則我們會發現圖靈機和lambda演算都假定了現實世界中無法滿足的條件。在真實的物理世界中，人類的認知總是有限的，所有的量都需要區分已知的部分和未知的部分，因此我們需要進行如下分解：

重新整理一下符號，我們就得到了一個適應范圍更加廣泛的計算模式

除了函數運算F(X)之外，這里出現了一個新的結構運算符⊕，它表示兩個元素之間的合成運算，并不是普通數值意義上的加法，同時引出了一個新的概念：差量△。△的特異之處在于，它必然包含某種負元素，F(X)與△合并在一起之后的結果并不一定是“增加”了輸出，而完全可能是“減少”。

在物理學中，差量△存在的必然性以及△包含逆元這一事實完全是不言而喻的，因為物理學的建模必須要考慮到兩個基本事實：

1. 世界是“測不準”的，噪聲永遠存在
2. 模型的復雜度要和問題內在的復雜度相匹配，它捕獲的是問題內核中穩定不變的趨勢及規律。

例如，對以下的數據 ​ ​

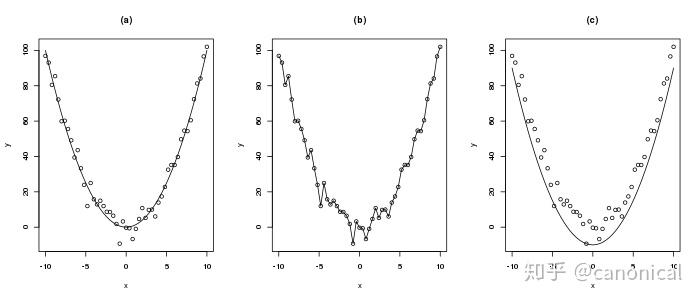
我們所建立的模型只能是類似圖(a)中的簡單曲線，圖(b)中的模型試圖精確擬合每一個數據點在數學上稱之為過擬合，它難以描述新的數據，而圖(c)中限制差量只能為正值則會極大的限制模型的描述精度。

以上是對Y=F(X)⊕△這一抽象計算模式的一個啟發式說明，下面我們將介紹在軟件構造領域落實這一計算模式的一種具體技術實現方案，筆者將其命名為可逆計算。 所謂可逆計算，是指系統化的應用如下公式指導軟件構造的一種技術路線

App : 所需要構建的目標應用程序
DSL: 領域特定語言（Domain Specific Language），針對特定業務領域定制的業務邏輯描述語言，也是所謂領域模型的文本表示形式
Generator : 根據領域模型提供的信息，反復應用生成規則可以推導產生大量的衍生代碼。實現方式包括獨立的代碼生成工具，以及基于元編程（Metaprogramming）的編譯期模板展開
Biz : 根據已知模型推導生成的邏輯與目標應用程序邏輯之間的差異被識別出來，并收集在一起，構成獨立的差量描述
aop_extends: 差量描述與模型生成部分通過類似面向切面編程（Aspect Oriented Programming）的技術結合在一起，這其中涉及到對模型生成部分的增加、修改、替換、刪除等一系列操作

DSL是對關鍵性領域信息的一種高密度的表達，它直接指導Generator生成代碼，這一點類似于圖靈計算通過輸入數據驅動機器執行內置指令。而如果把Generator看作是文本符號的替換生成，則它的執行和復合規則完全就是lambda演算的翻版。差量合并在某種意義上是一種很新奇的操作，因為它要求我們具有一種細致入微、無所不達的變化收集能力，能夠把散布系統各處的同階小量分離出來并合并在一起，這樣差量才具有獨立存在的意義和價值。同時，系統中必須明確建立逆元和逆運算的概念，在這樣的概念體系下差量作為“存在”與“不存在”的混合體才可能得到表達。

現有的軟件基礎架構如果不經過徹底的改造，是無法有效的實施可逆計算的。正如圖靈機模型孕育了C語言，Lambda演算促生了Lisp語言一樣，為了有效支持可逆計算，筆者提出了一種新的程序語言X語言，它內置了差量定義、生成、合并、拆分等關鍵特性，可以快速建立領域模型，并在領域模型的基礎上實現可逆計算。

為了實施可逆計算，我們必須要建立差量的概念。變化產生差量，差量有正有負，而且應該滿足下面三條要求：

1. 差量獨立存在
2. 差量相互作用
3. 差量具有結構

在第三節中筆者將會以Docker為實例說明這三條要求的重要性。

可逆計算的核心是“可逆”，這一概念與物理學中熵的概念息息相關，它的重要性其實遠遠超出了程序構造本身，在可逆計算的方法論來源一文中，筆者會對它有更詳細的闡述。

正如復數的出現擴充了代數方程的求解空間，可逆計算為現有的軟件構造技術體系補充了“可逆的差量合并”這一關鍵性技術手段，從而極大擴充了軟件復用的可行范圍，使得系統級的粗粒度軟件復用成為可能。同時在新的視角下，很多原先難以解決的模型抽象問題可以找到更加簡單的解決方案，從而大幅降低了軟件構造的內在復雜性。在第二節中筆者將會對此進行詳細闡述。

軟件開發雖然號稱是知識密集性的工作，但到目前為止，眾多一線程序員的日常中仍然包含著大量代碼拷貝/粘貼/修改的機械化手工操作內容，而在可逆計算理論中，代碼結構的修改被抽象為可自動執行的差量合并規則，因此通過可逆計算，我們可以為軟件自身的自動化生產創造基礎條件。筆者在可逆計算理論的基礎上，提出了一個新的軟件工業化生產模式NOP（Nop is nOt Programming），以非編程的方式批量生產軟件。NOP不是編程，但也不是不編程，它強調的是將業務人員可以直觀理解的邏輯與純技術實現層面的邏輯相分離，分別使用合適的語言和工具去設計，然后再把它們無縫的粘接在一起。筆者將在另一篇文章中對NOP進行詳細介紹。

可逆計算與可逆計算機有著同樣的物理學思想來源，雖然具體的技術內涵并不一致，但它們目標卻是統一的。正如云計算試圖實現計算的云化一樣，可逆計算和可逆計算機試圖實現的都是計算的可逆化。

二. 可逆計算對傳統理論的繼承和發展

（一）組件（Component）

軟件的誕生源于數學家研究希爾伯特第十問題時的副產品，早期軟件的主要用途也是數學物理計算，那時軟件中的概念無疑是抽象的、數學化的。隨著軟件的普及，越來越多應用軟件的研發催生了面向對象和組件化的方法論，它試圖弱化抽象思維，轉而貼近人類的常識，從人們的日常經驗中汲取知識，把業務領域中人們可以直觀感知的概念映射為軟件中的對象，仿照物質世界的生產制造過程從無到有、從小到大，逐步拼接組裝實現最終軟件產品的構造。

像框架、組件、設計模式、架構視圖等軟件開發領域中耳熟能詳的概念，均直接來自于建筑業的生產經驗。組件理論繼承了面向對象思想的精華，借助可復用的預制構件這一概念，創造了龐大的第三方組件市場，獲得了空前的技術和商業成功，即使到今天仍然是最主流的軟件開發指導思想。但是，組件理論內部存在著一個本質性的缺陷，阻礙了它把自己的成功繼續推進到一個新的高度。

我們知道，所謂復用就是對已有的制成品的重復使用。為了實現組件復用，我們需要找到兩個軟件中的公共部分，把它分離出來并按照組件規范整理成標準形式。但是，A和B的公共部分的粒度是比A和B都要小的，大量軟件的公共部分是比它們中任何一個的粒度都要小得多的。這一限制直接導致越大粒度的軟件功能模塊越難以被直接復用，組件復用存在理論上的極限。可以通過組件組裝復用60%-70%的工作量，但是很少有人能超過80%，更不用說實現復用度90%以上的系統級整體復用了。

為了克服組件理論的局限，我們需要重新認識軟件的抽象本質。軟件是在抽象的邏輯世界中存在的一種信息產品，信息并不是物質。抽象世界的構造和生產規律與物質世界是有著本質不同的。物質產品的生產總是有成本的，而復制軟件的邊際成本卻可以是0。將桌子從房間中移走在物質世界中必須要經過門或窗，但在抽象的信息空間中卻只需要將桌子的坐標從x改為-x而已。抽象元素之間的運算關系并不受眾多物理約束的限制，因此信息空間中最有效的生產方式不是組裝，而是掌握和制定運算規則。

如果從數學的角度重新去解讀面向對象和組件技術，我們會發現可逆計算可以被看作是組件理論的一個自然擴展。

• 面向對象 : 不等式 A > B
• 組件 : 加法 A = B + C
• 可逆計算 : 差量 Y = X + △Y

面向對象中的一個核心概念是繼承：派生類從基類繼承，自動具有基類的一切功能。例如老虎是動物的一種派生類，在數學上，我們可以說老虎(A)這個概念所包含的內容比動物(B)這個概念更多，老虎>動物（即A>B）。據此我們可以知道，動物這個概念所滿足的命題，老虎自然滿足， 例如動物會奔跑，老虎必然也會奔跑（ P(B) -> P(A) ）。程序中所有用到動物這一概念的地方都可以被替換為老虎（Liscov代換原則）。這樣通過繼承就將自動推理關系引入到軟件領域中來，在數學上這對應于不等式，也就是一種偏序關系。

面向對象的理論困境在于不等式的表達能力有限。對于不等式A > B，我們知道A比B多，但是具體多什么，我們并沒有辦法明確的表達出來。而對于 A > B， D > E這樣的情況，即使多出來的部分一模一樣，我們也無法實現這部分內容的重用。組件技術明確指出"組合優于繼承"，這相當于引入了加法

這樣就可以抽象出組件C進行重用。

沿著上述方向推演下去，我們很容易確定下一步的發展是引入“減法”，這樣才可以把 A = B + C看作是一個真正的方程，通過方程左右移項求解出

通過減法引入的“負組件”是一個全新的概念，它為軟件復用打開了一扇新的大門。

假設我們已經構建好了系統 X = D + E + F， 現在需要構建 Y = D + E + G。如果遵循組件的解決方案，則需要將X拆解為多個組件，然后更換組件F為G后重新組裝。而如果遵循可逆計算的技術路線，通過引入逆元 -F， 我們立刻得到

在不拆解X的情況下，通過直接追加一個差量△Y，即可將系統X轉化為系統Y。

組件的復用條件是“相同方可復用”，但在存在逆元的情況下，具有最大顆粒度的完整系統X在完全不改的情況下直接就可以被復用，軟件復用的范圍被拓展為“相關即可復用”，軟件復用的粒度不再有任何限制。組件之間的關系也發生了深刻的變化，不再是單調的構成關系，而成為更加豐富多變的轉化關系。

Y = X + △Y 這一物理圖像對于復雜軟件產品的研發具有非常現實的意義。X可以是我們所研發的軟件產品的基礎版本或者說主版本，在不同的客戶處部署實施時，大量的定制化需求被隔離到獨立的差量△Y中，這些定制的差量描述單獨存放，通過編譯技術與主版本代碼再合并到一起。主版本的架構設計和代碼實現只需要考慮業務領域內穩定的核心需求，不會受到特定客戶處偶然性需求的沖擊，從而有效的避免架構腐化。主版本研發和多個項目的實施可以并行進行，不同的實施版本對應不同的△Y，互不影響，同時主版本的代碼與所有定制代碼相互獨立，能夠隨時進行整體升級。

（二）模型驅動架構（Model Driven Architecture)

模型驅動架構（MDA）是由對象管理組織（Object Management Group，OMG）在2001年提出的軟件架構設計和開發方法，它被看作是軟件開發模式從以代碼為中心向以模型為中心轉變的里程碑，目前大部分所謂軟件開發平臺的理論基礎都與MDA有關。

MDA試圖提升軟件開發的抽象層次，直接使用建模語言（例如Executable UML）作為編程語言，然后通過使用類似編譯器的技術將高層模型翻譯為底層的可執行代碼。在MDA中，明確區分應用架構和系統架構，并分別用平臺無關模型PIM（Platform Independent Model）和平臺相關模型PSM（Platform Specific Model）來描述它們。PIM反映了應用系統的功能模型，它獨立于具體的實現技術和運行框架，而PSM則關注于使用特定技術（例如J2EE或者dotNet）實現PIM所描述的功能，為PIM提供運行環境。

使用MDA的理想場景是，開發人員使用可視化工具設計PIM，然后選擇目標運行平臺，由工具自動執行針對特定平臺和實現語言的映射規則，將PIM轉換為對應的PSM，并最終生成可執行的應用程序代碼。基于MDA的程序構造可以表述為如下公式

MDA的愿景是像C語言取代匯編那樣最終徹底消滅傳統編程語言。但經歷了這么多年發展之后，它仍未能夠在廣泛的應用領域中展現出相對于傳統編程壓倒性的競爭優勢。

事實上，目前基于MDA的開發工具在面對多變的業務領域時，總是難掩其內在的不適應性。根據本文第一節的分析，我們知道建模必須要考慮差量。而在MDA的構造公式中，左側的App代表了各種未知需求，而右側的Transformer和PIM的設計器實際上都主要由開發工具廠商提供，未知=已知這樣一個方程是無法持久保持平衡的。

目前，工具廠商的主要做法是提供大而全的模型集合，試圖事先預測用戶所有可能的業務場景。但是，我們知道“天下沒有免費的午餐”，模型的價值在于體現了業務領域中的本質性約束，沒有任何一個模型是所有場景下都最優的。預測需求會導致出現一種悖論: 模型內置假定過少，則無法根據用戶輸入的少量信息自動生成大量有用的工作，也無法防止用戶出現誤操作，模型的價值不明顯，而如果反之，模型假定很多，則它就會固化到某個特定業務場景，難以適應新的情況。

打開一個MDA工具的設計器，我們最經常的感受是大部分選項都不需要，也不知道是干什么用的，需要的選項卻到處找也找不到。

可逆計算對MDA的擴展體現為兩點：

1. 可逆計算中Generator和DSL都是鼓勵用戶擴充和調整的，這一點類似于面向語言編程（Language-oriented programming）。
2. 存在一個額外的差量定制機會，可以對整體生成結果進行精確的局部修正。

在筆者提出的NOP生產模式中，必須要包含一個新的關鍵組件：設計器的設計器。普通的程序員可以利用設計器的設計器快速設計開發自己的領域特定語言（DSL）及其可視化設計器，同時可以通過設計器的設計器對系統中的任意設計器進行定制調整，自由的增加或者刪除元素。

（三）面向切面編程（Aspect Oriented Programming)

面向切面（AOP）是與面向對象（OOP）互補的一種編程范式，它可以實現對那些橫跨多個對象的所謂橫切關注點（cross-cutting concern）的封裝。例如，需求規格中可能規定所有的業務操作都要記錄日志，所有的數據庫修改操作都要開啟事務。如果按照面向對象的傳統實現方式，需求中的一句話將會導致眾多對象類中陡然膨脹出現大量的冗余代碼，而通過AOP， 這些公共的“修飾性”的操作就可以被剝離到獨立的切面描述中。這就是所謂縱向分解和橫向分解的正交性。

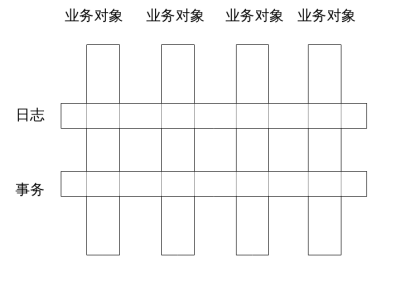
AOP本質上是兩個能力的組合：

1. 在程序結構空間中定位到目標切點（Pointcut）
2. 對局部程序結構進行修改，將擴展邏輯（Advice)編織(Weave)到指定位置。

定位依賴于存在良好定義的整體結構坐標系（沒有坐標怎么定位？），而修改依賴于存在良好定義的局部程序語義結構。目前主流的AOP技術的局限性在于，它們都是在面向對象的語境下表達的，而領域結構與對象實現結構并不總是一致的，或者說用對象體系的坐標去表達領域語義是不充分的。例如，申請人和審批人在領域模型中是需要明確區分的不同的概念，但是在對象層面卻可能都對應于同樣的Person類，使用AOP的很多時候并不能直接將領域描述轉換為切點定義和Advice實現。這種限制反映到應用層面，結果就是除了日志、事務、延遲加載、緩存等少數與特定業務領域無關的“經典”應用之外，我們找不到AOP的用武之地。

可逆計算需要類似AOP的定位和結構修正能力，但是它是在領域模型空間中定義這些能力的，因而大大擴充了AOP的應用范圍。特別是，可逆計算中領域模型自我演化產生的結構差量△能夠以類似AOP切面的形式得到表達。

我們知道，組件可以標識出程序中反復出現的“相同性”，而可逆計算可以捕獲程序結構的“相似性”。相同很罕見，需要敏銳的甄別，但是在任何系統中，有一種相似性都是唾手可得的，即動力學演化過程中系統與自身歷史快照之間的相似性。這種相似性在此前的技術體系中并沒有專門的技術表達形式。

通過縱向和橫向分解，我們所建立的概念之網存在于一個設計平面當中，當設計平面沿著時間軸演化時，很自然的會產生一個“三維”映射關系：后一時刻的設計平面可以看作是從前一時刻的平面增加一個差量映射（定制）而得到，而差量是定義在平面的每一個點上的。這一圖像類似于范疇論（Category Theory）中的函子（Functor）概念，可逆計算中的差量合并扮演了函子映射的角色。因此，可逆計算相當于擴展了原有的設計空間，為演化這一概念找到了具體的一種技術表現形式。

（四）軟件產品線（Software Product Line）

軟件產品線理論源于一個洞察，即在一個業務領域中，很少有軟件系統是完全獨特的，大量的軟件產品之間存在著形式和功能的相似性，可以歸結為一個產品家族，把一個產品家族中的所有產品（已存在的和尚未存在的）作為一個整體來研究、開發、演進，通過科學的方法提取它們的共性，結合有效的可變性管理，就有可能實現規模化、系統化的軟件復用，進而實現軟件產品的工業化生產。

軟件產品線工程采用兩階段生命周期模型，區分領域工程和應用工程。所謂領域工程，是指分析業務領域內軟件產品的共性，建立領域模型及公共的軟件產品線架構，形成可復用的核心資產的過程，即面向復用的開發（development for reuse）。而應用工程，其實質是使用復用來開發（ development with reuse），也就是利用已經存在的體系架構、需求、測試、文檔等核心資產來制造具體應用產品的生產活動。

卡耐基梅隆大學軟件工程研究所（CMU-SEI）的研究人員在2008年的報告中宣稱軟件產品線可以帶來如下好處：

1. 提升10倍以上生產率
2. 提升10倍以上產品質量
3. 縮減60%以上成本
4. 縮減87%以上人力需求
5. 縮減98%以上產品上市時間
6. 進入新市場的時間以月計，而不是年

軟件產品線描繪的理想非常美好：復用度90%以上的產品級復用、隨需而變的敏捷定制、無視技術變遷影響的領域架構、優異可觀的經濟效益等等。它所存在的唯一問題就是如何才能做到？盡管軟件產品線工程試圖通過綜合利用所有管理的和技術的手段，在組織級別策略性的復用一切技術資產（包括文檔、代碼、規范、工具等等），但在目前主流的技術體制下，發展成功的軟件產品線仍然面臨著重重困難。

可逆計算的理念與軟件產品線理論高度契合，它的技術方案為軟件產品線的核心技術困難---可變性管理帶來了新的解決思路。在軟件產品線工程中，傳統的可變性管理主要是適配、替換和擴展這三種方式：

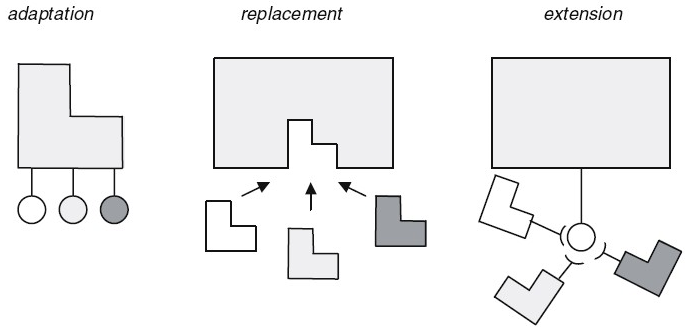
這三種方式都可以看作是向核心架構補充功能。但是可復用性的障礙不僅僅是來自于無法追加新的功能，很多時候也在于無法屏蔽原先已經存在的功能。傳統的適配技術等要求接口一致匹配，是一種剛性的對接要求，一旦失配必將導致不斷向上傳導應力，最終只能通過整體更換組件來解決問題。可逆計算通過差量合并為可變性管理補充了“消除”這一關鍵性機制，可以按需在領域模型空間中構建出柔性適配接口，從而有效的控制變化點影響范圍。

可逆計算中的差量雖然也可以被解釋為對基礎模型的一種擴展，但是它與插件擴展技術之間還是存在著明顯的區別。在平臺-插件這樣的結構中，平臺是最核心的主體，插件依附于平臺而存在，更像是一種補丁機制，在概念層面上是相對次要的部分。而在可逆計算中，通過一些形式上的變換，我們可以得到一個對稱性更高的公式：

如果把G看作是一種相對不變的背景知識，則形式上我們可以把它隱藏起來，定義一個更加高級的“括號”運算符，它類似于數學中的“內積”。在這種形式下，B和D是對偶的，B是對D的補充，而D也是對B的補充。同時，我們注意到G(D)是模型驅動架構的體現，模型驅動之所以有價值就在于模型D中發生的微小變化，可以被G放大為系統各處大量衍生的變化，因此G(D)是一種非線性變換，而B是系統中去除D所對應的非線性因素之后剩余的部分。當所有復雜的非線性影響因素都被剝離出去之后，最后剩下的部分B就有可能是簡單的，甚至能夠形成一種新的可獨立理解的領域模型結構(可以類比聲波與空氣的關系，聲波是空氣的擾動，但是不用研究空氣本體，我們就可以直接用正弦波模型來描述聲波)。

A = (B,D)的形式可以直接推廣到存在更多領域模型的情況

因為B、D、E等概念都是某種DSL所描述的領域模型，因此它們可以被解釋為A投影到特定領域模型子空間所產生的分量，也就是說，應用A可以被表示為一個“特征向量”（Feature Vector）， 例如

與軟件產品線中常用的面向特征編程（Feature Oriented Programming）相比，可逆計算的特征分解方案強調領域特定描述，特征邊界更加明確，特征合成時產生的概念沖突更容易處理。

特征向量本身構成更高維度的領域模型，它可以被進一步分解下去，從而形成一個模型級列，例如定義

, 并且假設D'可以繼續分解

，則可以得到

最終我們可以通過領域特征向量U'來描述D’，然后再通過領域特征向量D‘來描述原有的模型A。

可逆計算的這一構造策略類似于深度神經網絡，它不再局限于具有極多可調參數的單一模型，而是建立抽象層級不同、復雜性層級不同的一系列模型，通過逐步求精的方式構造出最終的應用。

在可逆計算的視角下，應用工程的工作內容變成了使用特征向量來描述軟件需求，而領域工程則負責根據特征向量描述來生成最終的軟件。

三. 初露端倪的差量革命

（一）Docker

Docker是2013年由創業公司dotCloud開源的應用容器引擎，它可以將任何應用及其依賴的環境打包成一個輕量級、可移植、自包含的容器（Container），并據此以容器為標準化單元創造了一種新型的軟件開發、部署和交付形式。

Docker一出世就秒殺了Google的親兒子lmctfy （Let Me Contain That For You）容器技術，同時也把Google的另一個親兒子Go語言迅速捧成了網紅，之后Docker的發展 更是一發而不可收拾。2014年開始一場Docker風暴席卷全球，以前所未有的力度推動了操作系統內核的變革，在眾多巨頭的跟風造勢下瞬間引爆容器云市場，真正從根本上改變了企業應用從開發、構建到部署、運行整個生命周期的技術形態。

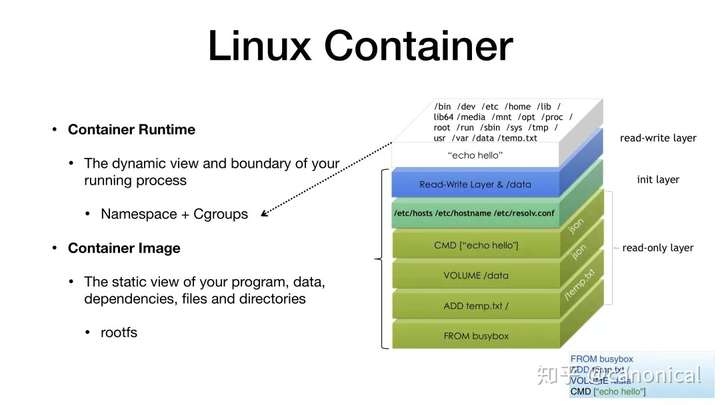
Docker技術的成功源于它對軟件運行時復雜性的本質性降低，而它的技術方案可以看作是可逆計算理論的一種特例。Docker的核心技術模式可以用如下公式進行概括

Dockerfile是構建容器鏡像的一種領域特定語言，例如

FROM ubuntu:16.04 
RUN useradd --user-group --create-home --shell /bin/bash work 
RUN apt-get update -y && apt-get install -y python3-dev 
COPY . /app RUN make /app  
ENV PYTHONPATH /FrameworkBenchmarks 
CMD python /app/app.py  
EXPOSE 8088

通過Dockerfile可以快速準確的描述容器所依賴的基礎鏡像，具體的構建步驟，運行時環境變量和系統配置等信息。

Docker應用程序扮演了可逆計算中Generator的角色，負責解釋Dockerfile，執行對應的指令來生成容器鏡像。

創造性的使用聯合文件系統（Union FS），是Docker的一個特別的創新之處。這種文件系統采用分層的構造方式，每一層構建完畢后就不會再發生改變，在后一層上進行的任何修改都只會記錄在自己這一層。例如，修改前一層的文件時會通過Copy-On-Write的方式復制一份到當前層，而刪除前一層的文件并不會真的執行刪除操作，而是僅在當前層標記該文件已刪除。Docker利用聯合文件系統來實現將多個容器鏡像合成為一個完整的應用，這一技術的本質正是可逆計算中的aop_extends操作。

Docker的英文是碼頭搬運工人的意思，它所搬運的容器也經常被人拿來和集裝箱做對比：標準的容器和集裝箱類似，使得我們可以自由的對它們進行傳輸/組合，而不用考慮容器中的具體內容。但是這種比較是膚淺的，甚至是誤導性的。集裝箱是靜態的、簡單的、沒有對外接口的，而容器則是動態的、復雜的、和外部存在著大量信息交互的。這種動態的復雜結構想和普通的靜態物件一樣封裝成所謂標準容器，其難度不可同日而語。如果沒有引入支持差量的文件系統，是無法構建出一種柔性邊界，實現邏輯分離的。

Docker所做的標準封裝其實虛擬機也能做到，甚至差量存儲機制在虛擬機中也早早的被用于實現增量備份，Docker與虛擬機的本質性不同到底在什么地方？回顧第一節中可逆計算對差量三個基本要求，我們可以清晰的發現Docker的獨特之處。

1. 差量獨立存在：Docker最重要的價值就在于通過容器封裝，拋棄了作為背景存在（必不可少，但一般情況下不需要了解），占據了99%的體積和復雜度的操作系統層。應用容器成為了可以獨立存儲、獨立操作的第一性的實體。輕裝上陣的容器在性能、資源占用、可管理性等方面完全超越了虛胖的虛擬機。
2. 差量相互作用：Docker容器之間通過精確受控的方式發生相互作用，可通過操作系統的namespace機制選擇性的實現資源隔離或者共享。而虛擬機的差量切片之間是沒有任何隔離機制的。
3. 差量具有結構：虛擬機雖然支持增量備份，但是人們卻沒有合適的手段去主動構造一個指定的差量切片出來。歸根結底，是因為虛擬機的差量定義在二進制字節空間中，而這個空間非常貧瘠，幾乎沒有什么用戶可以控制的構造模式。而Docker的差量是定義在差量文件系統空間中，這個空間繼承了Linux社區最豐富的歷史資源。每一條shell指令的執行結果最終反映到文件系統中都是增加/刪除/修改了某些文件，所以每一條shell指令都可以被看作是某個差量的定義。差量構成了一個異常豐富的結構空間，差量既是這個空間中的變換算符（shell指令），又是變換算符的運算結果。差量與差量相遇產生新的差量，這種生生不息才是Docker的生命力所在。

（二）React

2013年，也就是Docker發布的同一年，Facebook公司開源了一個革命性的Web前端框架React。React的技術思想非常獨特，它以函數式編程思想為基礎，結合一個看似異想天開的虛擬DOM（Virtual DOM)概念，引入了一整套新的設計模式，開啟了前端開發的新大航海時代。

React組件的核心是render函數，它的設計參考了后端常見的模板渲染技術，主要區別在于后端模板輸出的是HTML文本，而React組件的Render函數使用類似XML模板的JSX語法，通過編譯轉換在運行時輸出的是虛擬DOM節點對象。例如上面HelloMessage組件的render函數被翻譯后的結果類似于

每次重新生成DOM視圖的唯一問題是性能很低，特別是當前端交互操作眾多、狀態變化頻繁的時候。React的神來之筆是提出了基于虛擬DOM的diff算法，可以自動的計算兩個虛擬DOM樹之間的差量，狀態變化時只要執行虛擬Dom差量對應的DOM修改操作即可（更新真實DOM時會觸發樣式計算和布局計算，導致性能很低，而在JavaScript中操作虛擬DOM 的速度是非常快的）。整體策略可以表示為如下公式

顯然，這一策略也是可逆計算的一種特例。

只要稍微留意一下就會發現，最近幾年merge/diff/residual/delta等表達差量運算的概念越來越多的出現在軟件設計領域中。比如大數據領域的流計算引擎中，流與表之間的關系可以表示為

對表的增刪改查操作可以被編碼為事件流，而將表示數據變化的事件累積到一起就形成了數據表。

現代科學發端于微積分的發明，而微分的本質就是自動計算無窮小差量，而積分則是微分的逆運算，自動對無窮小量進行匯總合并。19世紀70年代，經濟學經歷了一場邊際革命，將微積分的思想引入經濟分析，在邊際這一概念之上重建了整個經濟學大廈。軟件構造理論發展到今天，已經進入一個瓶頸，也到了應該重新認識差量的時候。

四. 結語

筆者的專業背景是理論物理學，可逆計算源于筆者將物理學和數學的思想引入軟件領域的一種嘗試，它最早由筆者在2007年左右提出。一直以來，軟件領域對于自然規律的應用一般情況下都只限于"模擬"范疇，例如流體動力學模擬軟件，雖然它內置了人類所認知的最深刻的一些世界規律，但這些規律并沒有被用于指導和定義軟件世界自身的構造和演化，它們的指向范圍是軟件世界之外，而不是軟件世界自身。在筆者看來，在軟件世界中，我們完全可以站在“上帝的視角”，規劃和定義一系列的結構構造規律，輔助我們完成軟件世界的構建。而為了完成這一點，我們首先需要建立程序世界中的“微積分”。

類似于微積分，可逆計算理論的核心是將“差量”提升為第一性的概念，將全量看作是差量的一種特例（全量=單位元+全量）。傳統的程序世界中我們所表達的都只是“有”，而且是“所有”，差量只能通過全量之間的運算間接得到，它的表述和操縱都需要特殊處理，而基于可逆計算理論，我們首先應該定義所有差量概念的表達形式，然后再圍繞這些概念去建立整個領域概念體系。為了保證差量所在數學空間的完備性（差量之間的運算結果仍然需要是合法的差量），差量所表達的不能僅僅是“有”，而必須是“有”和“沒有”的一種混合體。也就是說差量必須是“可逆的”。可逆性具有非常深刻的物理學內涵，在基本的概念體系中內置這一概念可以解決很多非常棘手的軟件構造問題。

為了處理分布式問題，現代軟件開發體系已經接受了不可變數據的概念，而為了解決大粒度軟件復用問題，我們還需要接受不可變邏輯的概念（復用可以看作是保持原有邏輯不變，然后增加差量描述）。目前，業內已經逐步出現了一些富有創造性的主動應用差量概念的實踐，它們都可以在可逆計算的理論框架下得到統一的詮釋。筆者提出了一種新的程序語言X語言，它可以極大簡化可逆計算的技術實現。目前筆者已經基于X語言設計并實現了一系列軟件框架和生產工具，并基于它們提出了一種新的軟件生產范式（NOP）。