Quicksort

Quicksort is a fast sorting algorithm, which is used not only for educational purposes, but widely applied in practice. On the average, it has O(n log n) complexity, making quicksort suitable for sorting big data volumes. The idea of the algorithm is quite simple and once you realize it, you can write quicksort as fast as bubble sort.

Algorithm

The divide-and-conquer strategy is used in quicksort. Below the recursion step is described:

1. Choose a pivot value. We take the value of the middle element as pivot value, but it can be any value, which is in range of sorted values, even if it doesn't present in the array.
2. Partition. Rearrange elements in such a way, that all elements which are lesser than the pivot go to the left part of the array and all elements greater than the pivot, go to the right part of the array. Values equal to the pivot can stay in any part of the array. Notice, that array may be divided in non-equal parts.
3. Sort both parts. Apply quicksort algorithm recursively to the left and the right parts.

Partition algorithm in detail

There are two indices i and j and at the very beginning of the partition algorithm i points to the first element in the array andj points to the last one. Then algorithm moves i forward, until an element with value greater or equal to the pivot is found. Index j is moved backward, until an element with value lesser or equal to the pivot is found. If i ≤ j then they are swapped and i steps to the next position (i + 1), j steps to the previous one (j - 1). Algorithm stops, when i becomes greater than j.

After partition, all values before i-th element are less or equal than the pivot and all values after j-th element are greater or equal to the pivot.

Example. Sort {1, 12, 5, 26, 7, 14, 3, 7, 2} using quicksort.

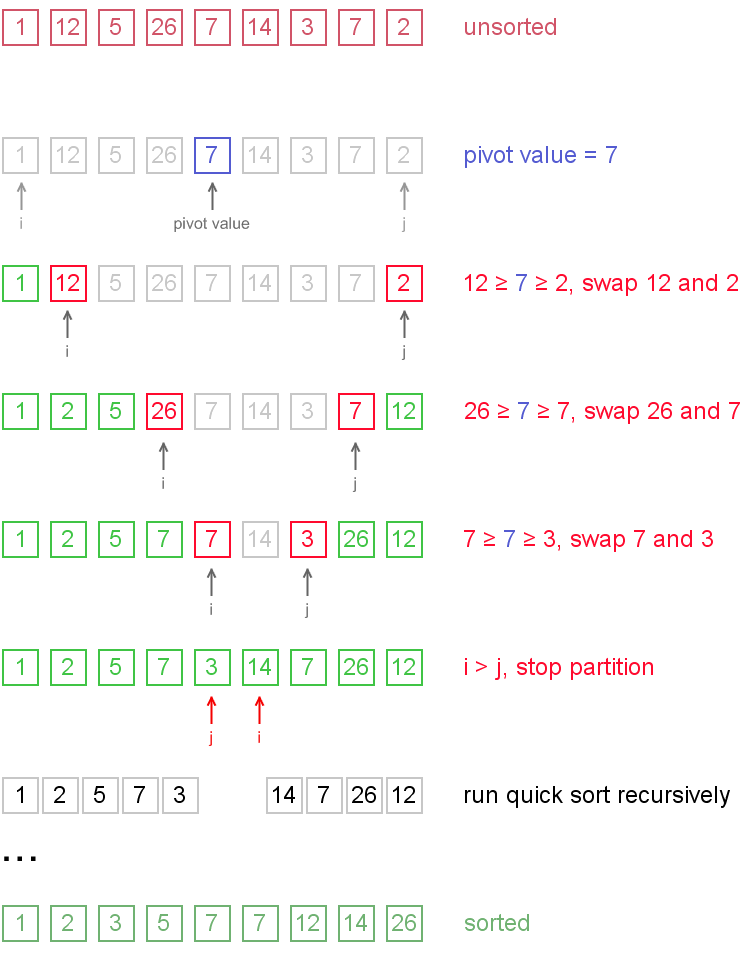
Notice, that we show here only the first recursion step, in order not to make example too long. But, in fact, {1, 2, 5, 7, 3} and {14, 7, 26, 12} are sorted then recursively.

Why does it work?

On the partition step algorithm divides the array into two parts and every element a from the left part is less or equal than every element b from the right part. Also a and b satisfy a ≤ pivot ≤ b inequality. After completion of the recursion calls both of the parts become sorted and, taking into account arguments stated above, the whole array is sorted.

Complexity analysis

On the average quicksort has O(n log n) complexity, but strong proof of this fact is not trivial and not presented here. Still, you can find the proof in [1]. In worst case, quicksort runs O(n²) time, but on the most "practical" data it works just fine and outperforms other O(n log n) sorting algorithms.

Code snippets

Java

int partition(int arr[], int left, int right)

{

     int i = left;

     int j = right;

     int temp;

    int  pivot = arr[(left+right)>>1];

     while(i<=j){

        while(arr[i]>=pivot){

            i++;

        }

        while(arr[j]<=pivot){

            j--;

       }

       if(i<=j){

           temp = arr[i];

           arr[i] = arr[j];

           arr[j] = temp;

           i++;

           j--;

       }

    }

    return i

}

 

void quickSort(int arr[], int left, int right) {

      int index = partition(arr, left, right);

      if(left<index-1){

         quickSort(arr,left,index-1);

      }

      if(index<right){

         quickSort(arr,index,right); 

      }

}

python

def quickSort(L,left,right) {

      i = left

      j = right

      if right-left <=1:

            return L

      pivot = L[(left + right) >>1];

      /* partition */

      while (i <= j) {

            while (L[i] < pivot)

                  i++;

            while (L[j] > pivot)

                  j--;

            if (i <= j) {

                  L[i],L[j] = L[j],L[i]

                  i++;

                  j--;

            }

      };

      /* recursion */

      if (left < j)

            quickSort(L, left, j);

      if (i < right)

            quickSort(L, i, right);

}

Insertion Sort

Insertion sort belongs to the O(n²) sorting algorithms. Unlike many sorting algorithms with quadratic complexity, it is actually applied in practice for sorting small arrays of data. For instance, it is used to improve quicksort routine. Some sources notice, that people use same algorithm ordering items, for example, hand of cards.

Algorithm

Insertion sort algorithm somewhat resembles selection sort. Array is imaginary divided into two parts - sorted one andunsorted one. At the beginning, sorted part contains first element of the array and unsorted one contains the rest. At every step, algorithm takes first element in the unsorted part and inserts it to the right place of the sorted one. Whenunsorted part becomes empty, algorithm stops. Sketchy, insertion sort algorithm step looks like this:

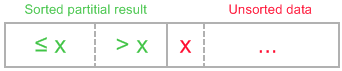
becomes

The idea of the sketch was originaly posted here.

Let us see an example of insertion sort routine to make the idea of algorithm clearer.

Example. Sort {7, -5, 2, 16, 4} using insertion sort.

The ideas of insertion

The main operation of the algorithm is insertion. The task is to insert a value into the sorted part of the array. Let us see the variants of how we can do it.

"Sifting down" using swaps

The simplest way to insert next element into the sorted part is to sift it down, until it occupies correct position. Initially the element stays right after the sorted part. At each step algorithm compares the element with one before it and, if they stay in reversed order, swap them. Let us see an illustration.

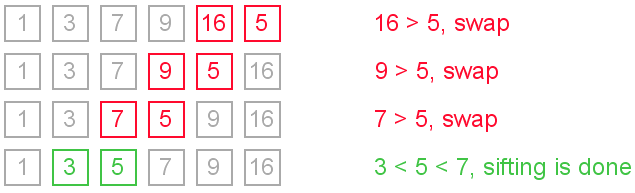
This approach writes sifted element to temporary position many times. Next implementation eliminates those unnecessary writes.

Shifting instead of swapping

We can modify previous algorithm, so it will write sifted element only to the final correct position. Let us see an illustration.

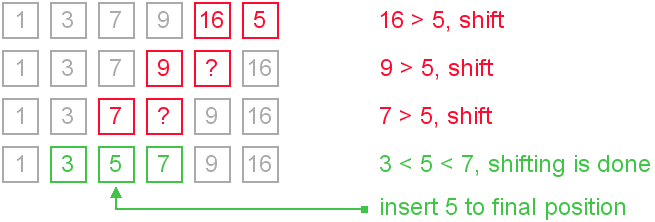
It is the most commonly used modification of the insertion sort.

Using binary search

It is reasonable to use binary search algorithm to find a proper place for insertion. This variant of the insertion sort is calledbinary insertion sort. After position for insertion is found, algorithm shifts the part of the array and inserts the element. This version has lower number of comparisons, but overall average complexity remains O(n²). From a practical point of view this improvement is not very important, because insertion sort is used on quite small data sets.

Complexity analysis

Insertion sort's overall complexity is O(n²) on average, regardless of the method of insertion. On the almost sorted arrays insertion sort shows better performance, up to O(n) in case of applying insertion sort to a sorted array. Number of writes is O(n²) on average, but number of comparisons may vary depending on the insertion algorithm. It is O(n²) when shifting or swapping methods are used and O(n log n) for binary insertion sort.

From the point of view of practical application, an average complexity of the insertion sort is not so important. As it was mentioned above, insertion sort is applied to quite small data sets (from 8 to 12 elements). Therefore, first of all, a "practical performance" should be considered. In practice insertion sort outperforms most of the quadratic sorting algorithms, like selection sort or bubble sort.

Insertion sort properties

• adaptive (performance adapts to the initial order of elements);
• stable (insertion sort retains relative order of the same elements);
• in-place (requires constant amount of additional space);
• online (new elements can be added during the sort).

Code snippets

We show the idea of insertion with shifts in Java implementation and the idea of insertion using python code snippet.

Java implementation

void insertionSort(int[] arr) {

      int i,j,newValue;

      for(i=1;i<arr.length;i++){

           newValue = arr[i];

           j=i;

           while(j>0&&arr[j-1]>newValue){

               arr[j] = arr[j-1];

               j--;

           }

           arr[j] = newValue;

}

Python implementation

void insertionSort(L) {

      for i in range(l,len(L)):

            j = i

            newValue = L[i]

            while j > 0 and  L[j - 1] >L[j]:

                 L[j] = L[j - 1]

                  j = j-1

            }

            L[j] = newValue

      }

}

Binary search algorithm

Generally, to find a value in unsorted array, we should look through elements of an array one by one, until searched value is found. In case of searched value is absent from array, we go through all elements. In average, complexity of such an algorithm is proportional to the length of the array.

Situation changes significantly, when array is sorted. If we know it, random access capability can be utilized very efficientlyto find searched value quick. Cost of searching algorithm reduces to binary logarithm of the array length. For reference, log₂(1 000 000) ≈ 20. It means, that in worst case, algorithm makes 20 steps to find a value in sorted array of a million elements or to say, that it doesn't present it the array.

Algorithm

Algorithm is quite simple. It can be done either recursively or iteratively:

1. get the middle element;
2. if the middle element equals to the searched value, the algorithm stops;
3. otherwise, two cases are possible:
   • searched value is less, than the middle element. In this case, go to the step 1 for the part of the array, before middle element.
   • searched value is greater, than the middle element. In this case, go to the step 1 for the part of the array, after middle element.

Now we should define, when iterations should stop. First case is when searched element is found. Second one is when subarray has no elements. In this case, we can conclude, that searched value doesn't present in the array.

Examples

Example 1. Find 6 in {-1, 5, 6, 18, 19, 25, 46, 78, 102, 114}.

Step 1 (middle element is 19 > 6):     -1  5  6  18  19  25  46  78  102  114

Step 2 (middle element is 5 < 6):      -1  5  6  18  19  25  46  78  102  114

Step 3 (middle element is 6 == 6):     -1  5  6  18  19  25  46  78  102  114

Example 2. Find 103 in {-1, 5, 6, 18, 19, 25, 46, 78, 102, 114}.

Step 1 (middle element is 19 < 103):   -1  5  6  18  19  25  46  78  102  114

Step 2 (middle element is 78 < 103):   -1  5  6  18  19  25  46  78  102  114

Step 3 (middle element is 102 < 103):  -1  5  6  18  19  25  46  78  102  114

Step 4 (middle element is 114 > 103):  -1  5  6  18  19  25  46  78  102  114

Step 5 (searched value is absent):     -1  5  6  18  19  25  46  78  102  114

Complexity analysis

Huge advantage of this algorithm is that it's complexity depends on the array size logarithmically in worst case. In practice it means, that algorithm will do at most log₂(n) iterations, which is a very small number even for big arrays. It can be proved very easily. Indeed, on every step the size of the searched part is reduced by half. Algorithm stops, when there are no elements to search in. Therefore, solving following inequality in whole numbers:

n / 2^iterations > 0

resulting in

iterations <= log₂(n).

It means, that binary search algorithm time complexity is O(log₂(n)).

Code snippets.

You can see recursive solution for Java and iterative for python below.

Java

int binarySearch(int[] array, int value, int left, int right) {

      if (left > right)

            return -1;

      int middle = left + (right-left) / 2;

      if (array[middle] == value)

            return middle;

      if (array[middle] > value)

            return binarySearch(array, value, left, middle - 1);

      else

            return binarySearch(array, value, middle + 1, right);           

}

Python

def biSearch(L,e,first,last):

      if last - first < 2: return L[first] == e or L[last] == e

      mid = first + (last-first)/2

      if L[mid] ==e: return True

      if L[mid]> e : 

            return biSearch(L,e,first,mid-1)

      return biSearch(L,e,mid+1,last)

      

Algorithm to merge sorted arrays

In the article we present an algorithm for merging two sorted arrays. One can learn how to operate with several arrays and master read/write indices. Also, the algorithm has certain applications in practice, for instance in merge sort.

Merge algorithm

Assume, that both arrays are sorted in ascending order and we want resulting array to maintain the same order. Algorithm to merge two arrays A[0..m-1] and B[0..n-1] into an array C[0..m+n-1] is as following:

1. Introduce read-indices i, j to traverse arrays A and B, accordingly. Introduce write-index k to store position of the first free cell in the resulting array. By default i = j = k = 0.
2. At each step: if both indices are in range (i < m and j < n), choose minimum of (A[i], B[j]) and write it toC[k]. Otherwise go to step 4.
3. Increase k and index of the array, algorithm located minimal value at, by one. Repeat step 2.
4. Copy the rest values from the array, which index is still in range, to the resulting array.

Enhancements

Algorithm could be enhanced in many ways. For instance, it is reasonable to check, if A[m - 1] < B[0] orB[n - 1] < A[0]. In any of those cases, there is no need to do more comparisons. Algorithm could just copy source arrays in the resulting one in the right order. More complicated enhancements may include searching for interleaving parts and run merge algorithm for them only. It could save up much time, when sizes of merged arrays differ in scores of times.

Complexity analysis

Merge algorithm's time complexity is O(n + m). Additionally, it requires O(n + m) additional space to store resulting array.

Code snippets

Java implementation

// size of C array must be equal or greater than

// sum of A and B arrays' sizes

public void merge(int[] A, int[] B, int[] C) {

      int i,j,k ;

      i = 0;

      j=0;

      k=0;

      m = A.length;

      n = B.length;

      while(i < m && j < n){

          if(A[i]<= B[j]){

              C[k] = A[i];

              i++;

          }else{

              C[k] = B[j];

              j++;

       }

       k++;

       while(i<m){

         C[k] = A[i]

         i++;

         k++;

      }

      while(j<n){

         C[k] = B[j] 

         j++;

          k++;

 }

Python  implementation

def merege(left,right):

    result = []

    i,j = 0

   while i< len(left) and j < len(right):

        if left[i]<= right[j]:

            result.append(left[i])

            i = i + 1

        else:

            result.append(right[j])

            j = j + 1

    while i< len(left):

           result.append(left[i])

           i = i + 1

    while　j< len(right):

           result.append(right[j])

           j = j + 1

    return result

  
MergSort:

Selection Sort

Selection sort is one of the O(n²) sorting algorithms, which makes it quite inefficient for sorting large data volumes. Selection sort is notable for its programming simplicity and it can over perform other sorts in certain situations (see complexity analysis for more details).

Algorithm

The idea of algorithm is quite simple. Array is imaginary divided into two parts - sorted one and unsorted one. At the beginning, sorted part is empty, while unsorted one contains whole array. At every step, algorithm finds minimal element in the unsorted part and adds it to the end of the sorted one. When unsorted part becomes empty, algorithmstops.

When algorithm sorts an array, it swaps first element of unsorted part with minimal element and then it is included to the sorted part. This implementation of selection sort in not stable. In case of linked list is sorted, and, instead of swaps, minimal element is linked to the unsorted part, selection sort is stable.

Let us see an example of sorting an array to make the idea of selection sort clearer.

Example. Sort {5, 1, 12, -5, 16, 2, 12, 14} using selection sort.

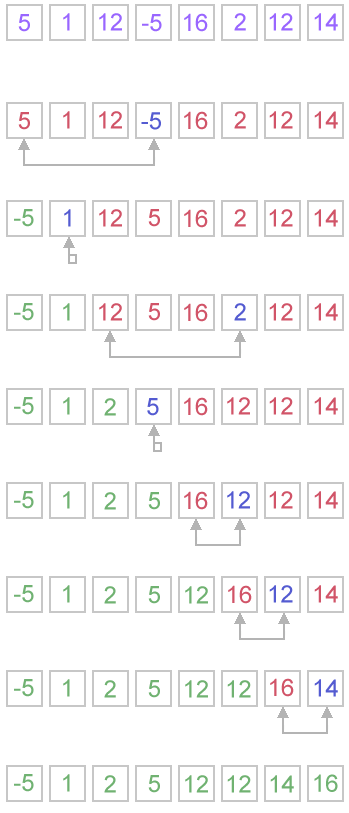
Complexity analysis

Selection sort stops, when unsorted part becomes empty. As we know, on every step number of unsorted elements decreased by one. Therefore, selection sort makes n steps (n is number of elements in array) of outer loop, before stop. Every step of outer loop requires finding minimum in unsorted part. Summing up, n + (n - 1) + (n - 2) + ... + 1, results in O(n²) number of comparisons. Number of swaps may vary from zero (in case of sorted array) to n - 1 (in case array was sorted in reversed order), which results in O(n) number of swaps. Overall algorithm complexity is O(n²).

Fact, that selection sort requires n - 1 number of swaps at most, makes it very efficient in situations, when write operation is significantly more expensive, than read operation.

Code snippets

Java

public void selectionSort(int[] arr) {

      int i, j, minIndex, tmp;

      int n = arr.length;

      for (i = 0; i < n - 1; i++) {

            minIndex = i;

            for (j = i + 1; j < n; j++)

                  if (arr[j] < arr[minIndex])

                        minIndex = j;

            if (minIndex != i) {

                  tmp = arr[i];

                  arr[i] = arr[minIndex];

                  arr[minIndex] = tmp;

            }

      }

}

Python

Bubble Sort

Bubble sort is a simple and well-known sorting algorithm. It is used in practice once in a blue moon and its main application is to make an introduction to the sorting algorithms. Bubble sort belongs to O(n²) sorting algorithms, which makes it quite inefficient for sorting large data volumes. Bubble sort is stable and adaptive.

Algorithm

1. Compare each pair of adjacent elements from the beginning of an array and, if they are in reversed order, swap them.
2. If at least one swap has been done, repeat step 1.

You can imagine that on every step big bubbles float to the surface and stay there. At the step, when no bubble moves, sorting stops. Let us see an example of sorting an array to make the idea of bubble sort clearer.

Example. Sort {5, 1, 12, -5, 16} using bubble sort.

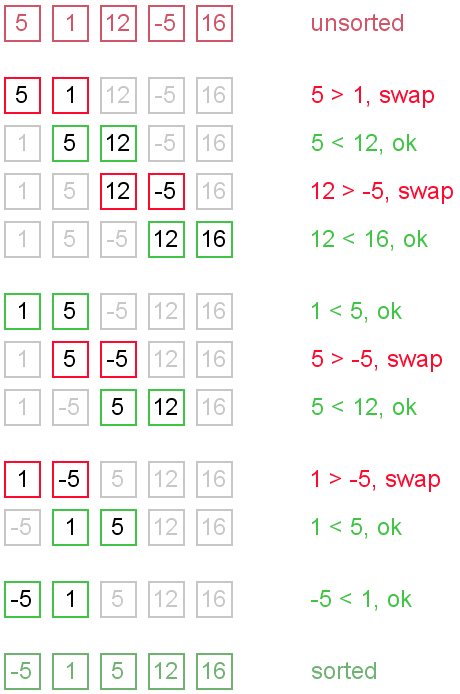
Complexity analysis

Average and worst case complexity of bubble sort is O(n²). Also, it makes O(n²) swaps in the worst case. Bubble sort is adaptive. It means that for almost sorted array it gives O(n) estimation. Avoid implementations, which don't check if the array is already sorted on every step (any swaps made). This check is necessary, in order to preserve adaptive property.

Turtles and rabbits

One more problem of bubble sort is that its running time badly depends on the initial order of the elements. Big elements (rabbits) go up fast, while small ones (turtles) go down very slow. This problem is solved in the Cocktail sort.

Turtle example. Thought, array {2, 3, 4, 5, 1} is almost sorted, it takes O(n²) iterations to sort an array. Element {1} is a turtle.

Rabbit example. Array {6, 1, 2, 3, 4, 5} is almost sorted too, but it takes O(n) iterations to sort it. Element {6} is a rabbit. This example demonstrates adaptive property of the bubble sort.

Code snippets

There are several ways to implement the bubble sort. Notice, that "swaps" check is absolutely necessary, in order to preserve adaptive property.

Java

public void bubbleSort(int[] arr) {

      boolean swapped = true;

      int j = 0;

      int tmp;

      while (swapped) {

            swapped = false;

            j++;

           for (int i = 0; i < arr.length - j; i++) {                               

                  if (arr[i] > arr[i + 1]) {                          

                        tmp = arr[i];

                        arr[i] = arr[i + 1];

                        arr[i + 1] = tmp;

                        swapped = true;

                  }

            }                

      }

}

Python

def bubbleSort(L) :

    swapped = True;

    while swapped:

        swapped = False

        for i in range(len(L)-1):

            if L[i]>L[i+1]:

                temp = L[i]

                L[i] = L[i+1]

                L[i+1] = temp

                swapped = True

Quicksort

Quicksort is a fast sorting algorithm, which is used not only for educational purposes, but widely applied in practice. On the average, it has O(n log n) complexity, making quicksort suitable for sorting big data volumes. The idea of the algorithm is quite simple and once you realize it, you can write quicksort as fast as bubble sort.

Algorithm

The divide-and-conquer strategy is used in quicksort. Below the recursion step is described:

1. Choose a pivot value. We take the value of the middle element as pivot value, but it can be any value, which is in range of sorted values, even if it doesn't present in the array.
2. Partition. Rearrange elements in such a way, that all elements which are lesser than the pivot go to the left part of the array and all elements greater than the pivot, go to the right part of the array. Values equal to the pivot can stay in any part of the array. Notice, that array may be divided in non-equal parts.
3. Sort both parts. Apply quicksort algorithm recursively to the left and the right parts.

Partition algorithm in detail

There are two indices i and j and at the very beginning of the partition algorithm i points to the first element in the array andj points to the last one. Then algorithm moves i forward, until an element with value greater or equal to the pivot is found. Index j is moved backward, until an element with value lesser or equal to the pivot is found. If i ≤ j then they are swapped and i steps to the next position (i + 1), j steps to the previous one (j - 1). Algorithm stops, when i becomes greater than j.

After partition, all values before i-th element are less or equal than the pivot and all values after j-th element are greater or equal to the pivot.

Example. Sort {1, 12, 5, 26, 7, 14, 3, 7, 2} using quicksort.

Notice, that we show here only the first recursion step, in order not to make example too long. But, in fact, {1, 2, 5, 7, 3} and {14, 7, 26, 12} are sorted then recursively.

Why does it work?

On the partition step algorithm divides the array into two parts and every element a from the left part is less or equal than every element b from the right part. Also a and b satisfy a ≤ pivot ≤ b inequality. After completion of the recursion calls both of the parts become sorted and, taking into account arguments stated above, the whole array is sorted.

Complexity analysis

On the average quicksort has O(n log n) complexity, but strong proof of this fact is not trivial and not presented here. Still, you can find the proof in [1]. In worst case, quicksort runs O(n²) time, but on the most "practical" data it works just fine and outperforms other O(n log n) sorting algorithms.

Code snippets

Java

int partition(int arr[], int left, int right)

{

     int i = left;

     int j = right;

     int temp;

    int  pivot = arr[(left+right)>>1];

     while(i<=j){

        while(arr[i]>=pivot){

            i++;

        }

        while(arr[j]<=pivot){

            j--;

       }

       if(i<=j){

           temp = arr[i];

           arr[i] = arr[j];

           arr[j] = temp;

           i++;

           j--;

       }

    }

    return i

}

 

void quickSort(int arr[], int left, int right) {

      int index = partition(arr, left, right);

      if(left<index-1){

         quickSort(arr,left,index-1);

      }

      if(index<right){

         quickSort(arr,index,right); 

      }

}

python

def quickSort(L,left,right) {

      i = left

      j = right

      if right-left <=1:

            return L

      pivot = L[(left + right) >>1];

      /* partition */

      while (i <= j) {

            while (L[i] < pivot)

                  i++;

            while (L[j] > pivot)

                  j--;

            if (i <= j) {

                  L[i],L[j] = L[j],L[i]

                  i++;

                  j--;

            }

      };

      /* recursion */

      if (left < j)

            quickSort(L, left, j);

      if (i < right)

            quickSort(L, i, right);

}

Insertion Sort

Insertion sort belongs to the O(n²) sorting algorithms. Unlike many sorting algorithms with quadratic complexity, it is actually applied in practice for sorting small arrays of data. For instance, it is used to improve quicksort routine. Some sources notice, that people use same algorithm ordering items, for example, hand of cards.

Algorithm

Insertion sort algorithm somewhat resembles selection sort. Array is imaginary divided into two parts - sorted one andunsorted one. At the beginning, sorted part contains first element of the array and unsorted one contains the rest. At every step, algorithm takes first element in the unsorted part and inserts it to the right place of the sorted one. Whenunsorted part becomes empty, algorithm stops. Sketchy, insertion sort algorithm step looks like this:

becomes

The idea of the sketch was originaly posted here.

Let us see an example of insertion sort routine to make the idea of algorithm clearer.

Example. Sort {7, -5, 2, 16, 4} using insertion sort.

The ideas of insertion

The main operation of the algorithm is insertion. The task is to insert a value into the sorted part of the array. Let us see the variants of how we can do it.

"Sifting down" using swaps

The simplest way to insert next element into the sorted part is to sift it down, until it occupies correct position. Initially the element stays right after the sorted part. At each step algorithm compares the element with one before it and, if they stay in reversed order, swap them. Let us see an illustration.

This approach writes sifted element to temporary position many times. Next implementation eliminates those unnecessary writes.

Shifting instead of swapping

We can modify previous algorithm, so it will write sifted element only to the final correct position. Let us see an illustration.

It is the most commonly used modification of the insertion sort.

Using binary search

It is reasonable to use binary search algorithm to find a proper place for insertion. This variant of the insertion sort is calledbinary insertion sort. After position for insertion is found, algorithm shifts the part of the array and inserts the element. This version has lower number of comparisons, but overall average complexity remains O(n²). From a practical point of view this improvement is not very important, because insertion sort is used on quite small data sets.

Complexity analysis

Insertion sort's overall complexity is O(n²) on average, regardless of the method of insertion. On the almost sorted arrays insertion sort shows better performance, up to O(n) in case of applying insertion sort to a sorted array. Number of writes is O(n²) on average, but number of comparisons may vary depending on the insertion algorithm. It is O(n²) when shifting or swapping methods are used and O(n log n) for binary insertion sort.

From the point of view of practical application, an average complexity of the insertion sort is not so important. As it was mentioned above, insertion sort is applied to quite small data sets (from 8 to 12 elements). Therefore, first of all, a "practical performance" should be considered. In practice insertion sort outperforms most of the quadratic sorting algorithms, like selection sort or bubble sort.

Insertion sort properties

• adaptive (performance adapts to the initial order of elements);
• stable (insertion sort retains relative order of the same elements);
• in-place (requires constant amount of additional space);
• online (new elements can be added during the sort).

Code snippets

We show the idea of insertion with shifts in Java implementation and the idea of insertion using python code snippet.

Java implementation

void insertionSort(int[] arr) {

      int i,j,newValue;

      for(i=1;i<arr.length;i++){

           newValue = arr[i];

           j=i;

           while(j>0&&arr[j-1]>newValue){

               arr[j] = arr[j-1];

               j--;

           }

           arr[j] = newValue;

}

Python implementation

void insertionSort(L) {

      for i in range(l,len(L)):

            j = i

            newValue = L[i]

            while j > 0 and  L[j - 1] >L[j]:

                 L[j] = L[j - 1]

                  j = j-1

            }

            L[j] = newValue

      }

}

Binary search algorithm

Generally, to find a value in unsorted array, we should look through elements of an array one by one, until searched value is found. In case of searched value is absent from array, we go through all elements. In average, complexity of such an algorithm is proportional to the length of the array.

Situation changes significantly, when array is sorted. If we know it, random access capability can be utilized very efficientlyto find searched value quick. Cost of searching algorithm reduces to binary logarithm of the array length. For reference, log₂(1 000 000) ≈ 20. It means, that in worst case, algorithm makes 20 steps to find a value in sorted array of a million elements or to say, that it doesn't present it the array.

Algorithm

Algorithm is quite simple. It can be done either recursively or iteratively:

1. get the middle element;
2. if the middle element equals to the searched value, the algorithm stops;
3. otherwise, two cases are possible:
   • searched value is less, than the middle element. In this case, go to the step 1 for the part of the array, before middle element.
   • searched value is greater, than the middle element. In this case, go to the step 1 for the part of the array, after middle element.

Now we should define, when iterations should stop. First case is when searched element is found. Second one is when subarray has no elements. In this case, we can conclude, that searched value doesn't present in the array.

Examples

Example 1. Find 6 in {-1, 5, 6, 18, 19, 25, 46, 78, 102, 114}.

Step 1 (middle element is 19 > 6):     -1  5  6  18  19  25  46  78  102  114

Step 2 (middle element is 5 < 6):      -1  5  6  18  19  25  46  78  102  114

Step 3 (middle element is 6 == 6):     -1  5  6  18  19  25  46  78  102  114

Example 2. Find 103 in {-1, 5, 6, 18, 19, 25, 46, 78, 102, 114}.

Step 1 (middle element is 19 < 103):   -1  5  6  18  19  25  46  78  102  114

Step 2 (middle element is 78 < 103):   -1  5  6  18  19  25  46  78  102  114

Step 3 (middle element is 102 < 103):  -1  5  6  18  19  25  46  78  102  114

Step 4 (middle element is 114 > 103):  -1  5  6  18  19  25  46  78  102  114

Step 5 (searched value is absent):     -1  5  6  18  19  25  46  78  102  114

Complexity analysis

Huge advantage of this algorithm is that it's complexity depends on the array size logarithmically in worst case. In practice it means, that algorithm will do at most log₂(n) iterations, which is a very small number even for big arrays. It can be proved very easily. Indeed, on every step the size of the searched part is reduced by half. Algorithm stops, when there are no elements to search in. Therefore, solving following inequality in whole numbers:

n / 2^iterations > 0

resulting in

iterations <= log₂(n).

It means, that binary search algorithm time complexity is O(log₂(n)).

Code snippets.

You can see recursive solution for Java and iterative for python below.

Java

int binarySearch(int[] array, int value, int left, int right) {

      if (left > right)

            return -1;

      int middle = left + (right-left) / 2;

      if (array[middle] == value)

            return middle;

      if (array[middle] > value)

            return binarySearch(array, value, left, middle - 1);

      else

            return binarySearch(array, value, middle + 1, right);           

}

Python

def biSearch(L,e,first,last):

      if last - first < 2: return L[first] == e or L[last] == e

      mid = first + (last-first)/2

      if L[mid] ==e: return True

      if L[mid]> e : 

            return biSearch(L,e,first,mid-1)

      return biSearch(L,e,mid+1,last)

      

Algorithm to merge sorted arrays

In the article we present an algorithm for merging two sorted arrays. One can learn how to operate with several arrays and master read/write indices. Also, the algorithm has certain applications in practice, for instance in merge sort.

Merge algorithm

Assume, that both arrays are sorted in ascending order and we want resulting array to maintain the same order. Algorithm to merge two arrays A[0..m-1] and B[0..n-1] into an array C[0..m+n-1] is as following:

1. Introduce read-indices i, j to traverse arrays A and B, accordingly. Introduce write-index k to store position of the first free cell in the resulting array. By default i = j = k = 0.
2. At each step: if both indices are in range (i < m and j < n), choose minimum of (A[i], B[j]) and write it toC[k]. Otherwise go to step 4.
3. Increase k and index of the array, algorithm located minimal value at, by one. Repeat step 2.
4. Copy the rest values from the array, which index is still in range, to the resulting array.

Enhancements

Algorithm could be enhanced in many ways. For instance, it is reasonable to check, if A[m - 1] < B[0] orB[n - 1] < A[0]. In any of those cases, there is no need to do more comparisons. Algorithm could just copy source arrays in the resulting one in the right order. More complicated enhancements may include searching for interleaving parts and run merge algorithm for them only. It could save up much time, when sizes of merged arrays differ in scores of times.

Complexity analysis

Merge algorithm's time complexity is O(n + m). Additionally, it requires O(n + m) additional space to store resulting array.

Code snippets

Java implementation

// size of C array must be equal or greater than

// sum of A and B arrays' sizes

public void merge(int[] A, int[] B, int[] C) {

      int i,j,k ;

      i = 0;

      j=0;

      k=0;

      m = A.length;

      n = B.length;

      while(i < m && j < n){

          if(A[i]<= B[j]){

              C[k] = A[i];

              i++;

          }else{

              C[k] = B[j];

              j++;

       }

       k++;

       while(i<m){

         C[k] = A[i]

         i++;

         k++;

      }

      while(j<n){

         C[k] = B[j] 

         j++;

          k++;

 }

Python  implementation

def merege(left,right):

    result = []

    i,j = 0

   while i< len(left) and j < len(right):

        if left[i]<= right[j]:

            result.append(left[i])

            i = i + 1

        else:

            result.append(right[j])

            j = j + 1

    while i< len(left):

           result.append(left[i])

           i = i + 1

    while　j< len(right):

           result.append(right[j])

           j = j + 1

    return result

  
MergSort:

Selection Sort

Selection sort is one of the O(n²) sorting algorithms, which makes it quite inefficient for sorting large data volumes. Selection sort is notable for its programming simplicity and it can over perform other sorts in certain situations (see complexity analysis for more details).

Algorithm

The idea of algorithm is quite simple. Array is imaginary divided into two parts - sorted one and unsorted one. At the beginning, sorted part is empty, while unsorted one contains whole array. At every step, algorithm finds minimal element in the unsorted part and adds it to the end of the sorted one. When unsorted part becomes empty, algorithmstops.

When algorithm sorts an array, it swaps first element of unsorted part with minimal element and then it is included to the sorted part. This implementation of selection sort in not stable. In case of linked list is sorted, and, instead of swaps, minimal element is linked to the unsorted part, selection sort is stable.

Let us see an example of sorting an array to make the idea of selection sort clearer.

Example. Sort {5, 1, 12, -5, 16, 2, 12, 14} using selection sort.

Complexity analysis

Selection sort stops, when unsorted part becomes empty. As we know, on every step number of unsorted elements decreased by one. Therefore, selection sort makes n steps (n is number of elements in array) of outer loop, before stop. Every step of outer loop requires finding minimum in unsorted part. Summing up, n + (n - 1) + (n - 2) + ... + 1, results in O(n²) number of comparisons. Number of swaps may vary from zero (in case of sorted array) to n - 1 (in case array was sorted in reversed order), which results in O(n) number of swaps. Overall algorithm complexity is O(n²).

Fact, that selection sort requires n - 1 number of swaps at most, makes it very efficient in situations, when write operation is significantly more expensive, than read operation.

Code snippets

Java

public void selectionSort(int[] arr) {

      int i, j, minIndex, tmp;

      int n = arr.length;

      for (i = 0; i < n - 1; i++) {

            minIndex = i;

            for (j = i + 1; j < n; j++)

                  if (arr[j] < arr[minIndex])

                        minIndex = j;

            if (minIndex != i) {

                  tmp = arr[i];

                  arr[i] = arr[minIndex];

                  arr[minIndex] = tmp;

            }

      }

}

Python