Suppose n1, n2, …, nk are positive integers which are pairwise coprime. Then, for any given integers a1,a2, …, ak, there exists an integer x solving the system of simultaneous congruences
Furthermore, all solutions x to this system are congruent modulo the product N = n1n2…nk.
Hence  for all
for all  , if and only if
, if and only if  .
.
Sometimes, the simultaneous congruences can be solved even if the ni's are not pairwise coprime. A solution x exists if and only if:
All solutions x are then congruent modulo the least common multiple of the ni.
Versions of the Chinese remainder theorem were also known to Brahmagupta (7th century), and appear in Liber Abaci (1202).
[edit] A constructive algorithm to find the solution
This algorithm only treats the situations where the ni's are coprime. The method of successive substitution can often yield solutions to simultaneous congruences, even when the moduli are not pairwise coprime.
Suppose, as above, that a solution is needed to the system of congruences:
Again, to begin, the product  is defined. Then a solution x can be found as follows.
is defined. Then a solution x can be found as follows.
For each i the integers ni and N / ni are coprime. Using the extended Euclidean algorithm we can therefore find integers ri and si such that rini + siN / ni = 1. Then, choosing the label ei = siN / ni, the above expression becomes:
Consider ei. The above equation guarantees that its remainder, when divided by ni, must be 1. On the other hand, since it is formed as siN / ni, the presence of N guarantees that it's evenly divisible by any nj so long as 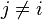 .
.
Because of this, combined with the multiplication rules allowed in congruences, one solution to the system of simultaneous congruences is:
For example, consider the problem of finding an integer x such that
Using the extended Euclidean algorithm for 3 and 4×5 = 20, we find (−13) × 3 + 2 × 20 = 1, i.e. e1 = 40. Using the Euclidean algorithm for 4 and 3×5 = 15, we get (−11) × 4 + 3 × 15 = 1. Hence, e2 = 45. Finally, using the Euclidean algorithm for 5 and 3×4 = 12, we get 5 × 5 + (−2) × 12 = 1, meaning e3 = −24. A solution x is therefore 2 × 40 + 3 × 45 + 1 × (−24) = 191. All other solutions are congruent to 191 modulo 60, (3 × 4 × 5 = 60) which means that they are all congruent to 11 modulo 60.
NOTE: There are multiple implementations of the extended Euclidean algorithm which will yield different sets of e1, e2, and e3. These sets however will produce the same solution i.e. 11 modulo 60.
extended Enclidean algorithm
[edit] Informal formulation of the algorithm
| Dividend | Divisor | Quotient | Remainder |
|---|---|---|---|
| 120 | 23 | 5 | 5 |
| 23 | 5 | 4 | 3 |
| 5 | 3 | 1 | 2 |
| 3 | 2 | 1 | 1 |
| 2 | 1 | 2 | 0 |
It is assumed that the reader is already familiar with .
To illustrate the extension of the Euclid's algorithm, consider the computation of gcd(120, 23), which is shown on the table on the left. Notice that the quotient in each division is recorded as well alongside the remainder.
In this case, the remainder in the fourth line (which is equal to 1) indicates that the gcd is 1; that is, 120 and 23 are coprime (also called relatively prime). For the sake of simplicity, the example chosen is a coprime pair; but the more general case of gcd other than 1 also works similarly.
There are two methods to proceed, both using the division algorithm, which will be discussed separately.
[edit] The iterative method
This method computes expressions of the form ri = axi + byi for the remainder in each step i of the Euclidean algorithm. Each modulus can be written in terms of the previous two remainders and their whole quotient as follows:
By substitution, this gives:
The first two values are the initial arguments to the algorithm:
- r1 = a = a(1) + b(0)
- r2 = b = a(0) + b(1)
The expression for the last non-zero remainder gives the desired results since this method computes every remainder in terms of a and b, as desired.
Example: Compute the GCD of 120 and 23.
The computation proceeds as follows:
| Step | Quotient | Remainder | Substitute | Combine terms | |
|---|---|---|---|---|---|
| 1 | 120 | 120 = 120 * 1 + 23 * 0 | |||
| 2 | 23 | 23 = 120 * 0 + 23 * 1 | |||
| 3 | 5 | 5 = 120 - 23 * 5 | 5 = (120 * 1 + 23 * 0) - (120 * 0 + 23 * 1) * 5 | 5 = 120 * 1 + 23 * -5 | |
| 4 | 4 | 3 = 23 - 5 * 4 | 3 = (120 * 0 + 23 * 1) - (120 * 1 + 23 * -5) * 4 | 3 = 120 * -4 + 23 * 21 | |
| 5 | 1 | 2 = 5 - 3 * 1 | 2 = (120 * 1 + 23 * -5) - (120 * -4 + 23 * 21) * 1 | 2 = 120 * 5 + 23 * -26 | |
| 6 | 1 | 1 = 3 - 2 * 1 | 1 = (120 * -4 + 23 * 21) - (120 * 5 + 23 * -26) * 1 | 1 = 120 * -9 + 23 * 47 | |
| 7 | 2 | 0 | End of algorithm | ||
The last line reads 1 = −9×120 + 47×23, which is the required solution: x = −9 and y = 47.
This also means that −9 is the multiplicative inverse of 120 modulo 23, and that 47 is the multiplicative inverse of 23 modulo 120.
- −9 × 120 ≡ 1 mod 23 and also 47 × 23 ≡ 1 mod 120.
[edit] The recursive method
This method attempts to solve the original equation directly, by reducing the dividend and divisor gradually, from the first line to the last line, which can then be substituted with trivial value and work backward to obtain the solution.
Consider the original equation:
| 120 | x | + | 23 | y | = | 1 |
| (5×23+5) | x | + | 23 | y | = | 1 |
| 23 | (5x+y) | + | 5 | x | = | 1 |
| ... | ||||||
| 1 | a | + | 0 | b | = | 1 |
Notice that the equation remains unchanged after decomposing the original dividend in terms of the divisor plus a remainder, and then regrouping terms. If we have a solution to the equation in the second line, then we can work backward to find x and y as required. Although we don't have the solution yet to the second line, notice how the magnitude of the terms decreased (120 and 23 to 23 and 5). Hence, if we keep applying this, eventually we'll reach the last line, which obviously has (1,0) as a trivial solution. Then we can work backward and gradually find out x and y.
| Dividend | = | Quotient | x | Divisor | + | Remainder |
|---|---|---|---|---|---|---|
| 120 | = | 5 | x | 23 | + | 5 |
| 23 | = | 4 | x | 5 | + | 3 |
| ... | ||||||
For the purpose of explaining this method, the full working will not be shown. Instead some of the repeating steps will be described to demonstrate the principle behind this method.
Start by rewriting each line from the first table with division algorithm, focusing on the dividend this time (because we'll be substituting the dividend).
| 120 | x0 | + | 23 | y0 | = | 1 |
| (5×23+5) | x0 | + | 23 | y0 | = | 1 |
| 23 | (5x0+y0) | + | 5 | x0 | = | 1 |
| 23 | x1 | + | 5 | y1 | = | 1 |
| (4×5+3) | x1 | + | 5 | y1 | = | 1 |
| 5 | (4x1+y1) | + | 3 | x1 | = | 1 |
| 5 | x2 | + | 3 | y2 | = | 1 |
|
[edit] The table method
The table method is probably the simplest method to carry out with a pencil and paper. It is similar to the recursive method, although it does not directly require algebra to use and only requires working in one direction. The main idea is to think of the equation chain as a sequence of divisors . In the running example we have the sequence 120, 23, 5, 3, 2, 1. Any element in this chain can be written as a linear combination of the original x and y, most notably, the last element, gcd(x,y), can be written in this way. The table method involves keeping a table of each divisor, written as a linear combination. The algorithm starts with the table as follows:
| a | b | d |
| 1 | 0 | 120 |
| 0 | 1 | 23 |
The elements in the d column of the table will be the divisors in the sequence. Each di can be represented as the linear combination . The a and b values are obvious for the first two rows of the table, which represent x and y themselves. To compute di for any i > 2, notice that . Suppose . Then it must be that and . This is easy to verify algebraically with a simple substitution.
Actually carrying out the table method though is simpler than the above equations would indicate. To find the third row of the table in the example, just notice that 120 divided by 23 goes 5 times plus a remainder. This gives us k, the multiplying factor for this row. Now, each value in the table is the value two rows above it, minus k times the value immediately above it. This correctly leads to , , and . After repeating this method to find each line of the table (note that the remainder written in the table and the multiplying factor are two different numbers!), the final values for a and b will solve :
| a | b | d |
| 1 | 0 | 120 |
| 0 | 1 | 23 |
| 1 | -5 | 5 |
| -4 | 21 | 3 |
| 5 | -26 | 2 |
| -9 | 47 | 1 |
This method is simple, requiring only the repeated application of one rule, and leaves the answer in the final row of the table with no backtracking. Note also that if you end up with a negative number as the answer for the factor of, in this case b, you will then need to add the modulus in order to make it work as a modular inverse (instead of just taking the absolute value of b). I.e. if it returns a negative number, don't just flip the sign, but add in the other number to make it work. Otherwise it will give you the modular inverse yielding negative one.
εè²ηÄÉηßΘΫ{?/h3>
εä®φĹηß³εà£γ°½φ≥ïεè·φ€âφïàε€ΑηßΘφ≠Λι½°ιΔ‰ψIJδΗ΄ιùΔφàëδΜ§φ¨âγÖßεä®φĹηß³εà£γ°½φ≥ïη°Ψη°Γγö³εê³δΗΣφ≠ΞιΣΛφùΞη°Ψη°ΓδΗÄδΗΣηßΘφ≠Λι½°ιΔ‰γö³φ€âφïàΫé½φ≥ïψÄ?/p>
1.φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½γö³γΜ™φû?/h4>
ηßΘφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ι½°ιΔ‰φ½Εφ€Äε°“é(gu®©)‰™φɦ_àΑγö³γ°½φ≥ïφ‰·ΫIΖδ΄Dφê€γÉΠ(ch®≥)φ≥ïοΦ¨εç¦_·ΙXγö³φ·èδΗÄδΗΣε≠êεΚèεà½εQ¨φΘÄφüΞε°Éφ‰·εêΠδΙüφ‰·Yγö³ε≠êεΚèεà½εQ¨δΜéηĨγΓ°ε°öε°Éφ‰·εêΠδΗΚX壨Yγö³εÖ§εÖ±ε≠êεΚèεà½εQ¨εΤà δΗîε€®΄²Ä(g®®)φüΞηΩ΅ΫE΄δΗ≠ιÄâε΅Κφ€ÄιïΩγö³εÖ§εÖ±ε≠êεΚèεà½ψIJXγö³φâÄφ€âε≠êεΚèεà½ιÉΫφΘÄφüΞηΩ΅εêéεç≥εè·φ±²ε΅ΚX壨Yγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψIJXγö³δΗÄδΗΣε≠êεΚèεà½γ¦ΗεΚîδΚéδΗ΄φ†΅εΚèεà½{1, 2, …, m}γö³δΗÄδΗΣε≠êεΚèεà½εQ¨ε¦†φ≠ΛοΦ¨XεÖ±φ€â2mδΗΣδΗçεê¨ε≠êεΚèεà½εQ¨δΜéηĨγ©ΖδΗΨφê€γ¥Δφ≥ïι€ÄηΠ¹φ¨΅φïΑφ½Ει½¥ψÄ?/p>
δΚ΄ε°ûδΗäοΦ¨φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ι½°ιΔ‰?sh®¥)Ιüφ€âφ€ÄδΦ‰ε≠êΨl™φû³φÄßη¥®εQ¨ε¦†δΗΚφàëδΜ§φ€âεΠ²δΗ΄ε°öγêÜεQ?/p>
ε°öγêÜ: LCSγö³φ€ÄδΦ‰ε≠êΨl™φû³φÄßη¥®
η°ë÷Κèεà½X=<x1, x2, …, xm>壨Y=<y1, y2, …, yn>γö³δΗÄδΗΣφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½Z=<z1, z2, …, zk>εQ¨εàôεQ?/p>
- η΄Ξxm=ynεQ¨εàôzk=xm=ynδΗîZk-1φ‰·Xm-1壨Yn-1γö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½εQ?
- η΄Ξxm≠ynδΗîzk≠xm εQ?/sub>εàôZφ‰·Xm-1壨Yγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½εQ?
- η΄Ξxm≠ynδΗîzk≠yn εQ¨εàôZφ‰·X壨Yn-1γö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψÄ?
εÖΕδΗ≠Xm-1=<x1, x2, …, xm-1>εQ¨Yn-1=<y1, y2, …, yn-1>εQ¨Zk-1=<z1, z2, …, zk-1>ψÄ?/p>
η·¹φ‰é
- γî®εèçη·¹φ≥ïψIJη΄Ξzk≠xmεQ¨εàô<z1, z2, …, zk ,xm >φ‰·X壨Yγö³ιïΩεΚΠδΊ™(f®¥)kεç?γö³εÖ§εÖ±ε≠êεΚèεà½ψIJηΩôδΗéZφ‰·X壨Yγö³δΗÄδΗΣφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½γü¦γ¦ΨψÄ²ε¦†φ≠ΛοΦ¨εΩÖφ€âzk=xm=ynψIJγî±φ≠Λεè·γüΞZk-1φ‰·Xm-1壨Yn-1γö³δΗÄδΗΣιïΩεΚΠδΊ™(f®¥)k-1γö³εÖ§εÖ±ε≠êεΚèεà½ψIJη΄ΞXm-1壨Yn-1φ€âδΗÄδΗΣιïΩεΚΠεΛßδΚék-1γö³εÖ§εÖ±ε≠êεΚèεà½WεQ¨εàôû°Üxmεä†ε€®εÖΕεΑΨιÉ®εΑÜδΚßγîüX壨Yγö³δΗÄδΗΣιïΩεΚΠεΛßδΚékγö³εÖ§εÖ±ε≠êεΚèεà½ψIJφ≠ΛδΗΚγü¦γ¦ΨψIJφïÖZk-1φ‰·Xm-1壨Yn-1γö³δΗÄδΗΣφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψÄ?
- γîΉÉΚézk≠xmεQ¨Zφ‰·Xm-1壨Yγö³δΗÄδΗΣεÖ§εÖ±ε≠êεΚèεà½ψIJη΄ΞXm-1壨Yφ€âδΗÄδΗΣιïΩεΚΠεΛßδΚékγö³εÖ§εÖ±ε≠êεΚèεà½WεQ¨εàôWδΙüφ‰·X壨Yγö³δΗÄδΗΣιïΩεΚΠεΛßδΚékγö³εÖ§εÖ±ε≠êεΚèεà½ψIJηΩôδΗéZφ‰·X壨Yγö³δΗÄδΗΣφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½γü¦γ¦ΨψIJγî±φ≠Λεç≥γüΞZφ‰·Xm-1壨Yγö³δΗÄδΗΣφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψÄ?
- δΗ?2.Ψc÷MΦΦψÄ?
‰qôδΗΣε°öγêÜεëäη·âφàëδΜ§εQ¨δΗΛδΗΣεΚèεà½γö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ε¨ÖεêΪδΚ?ji®Θn)ηΩôδΗΛδΗΣεΚèεà½γö³εâçΨ~Äγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψÄ²ε¦†φ≠ΛοΦ¨φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ι½°ιΔ‰εÖδh€âφ€ÄδΦ‰ε≠êΨl™φû³φÄßη¥®ψÄ?/p>
2.ε≠êι½°ιΔ‰γö³ιÄ£εΫ£Ψl™φû³
γî±φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ι½°ιΔ‰γö³φ€ÄδΦ‰ε≠êΨl™φû³φÄßη¥®εè·γüΞεQ¨ηΠ¹φâë÷΅ΚX=<x1, x2, …, xm>壨Y=<y1, y2, …, yn>γö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½εQ¨εè·φ¨âδΜΞδΗ΄φ•ΙεΦèιÄ£εΫ£ε€ΑηΩ¦ηΓ¨οΦö(x®§)εΫ™xm=ynφ½”ûΦ¨φâë÷΅ΚXm-1壨Yn-1γö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½εQ¨γ³Εεêéε€®εÖΕεΑΨιÉ®εä†δΗäxm(=yn)εç¦_è·εΨ½X壨Yγö³δΗÄδΗΣφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψIJεΫ™xm≠ynφ½”ûΦ¨εΩÖιΓΜηßΘδΗΛδΗΣε≠êι½°ιΔ‰εQ¨εç≥φâë÷΅ΚXm-1壨Yγö³δΗÄδΗΣφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½εè?qi®Δng)X壨Yn-1γö³δΗÄδΗΣφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψIJηΩôδΗΛδΗΣεÖ§εÖ±ε≠êεΚèεà½δΗ≠ηΨÉιïΩηÄÖεç≥δΗΚX壨Yγö³δΗÄδΗΣφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψÄ?/p>
γî±φ≠ΛιÄ£εΫ£Ψl™φû³ε°“é(gu®©)‰™γ€΄εàΑφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ι½°ιΔ‰εÖδh€âε≠êι½°ιΔ‰ι΅çεè†φÄßη¥®ψIJδΨ΄εΠ²οΦ¨ε€®η°ΓΫé½X壨Yγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½φ½”ûΦ¨εè·ηÉΫηΠ¹η°ΓΫé½ε΅ΚX壨Yn-1εè?qi®Δng)Xm-1壨Yγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψIJηĨηΩôδΗΛδΗΣε≠êι½°ιΔ‰ιÉΫε¨ÖεêΪδΗÄδΗΣεÖ§εÖ±ε≠êι½°ιΔ‰εQ¨εç≥η°Γγ°½Xm-1壨Yn-1γö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψÄ?/p>
δΗéγü©ι‰ΒηΩûδΙ‰γß·φ€ÄδΦ‰η°ΓΫé½φ§ΓεΚèι½°ιΔ‰γ±ΜδΦϊ|Φ¨φàëδΜ§φùΞεΨèγΪ΄ε≠êι½°ιΔ‰γö³φ€ÄδΦ‰εÄΦγö³ιÄ£εΫ£εÖ≥γ≥ΜψIJγî®c[i,j]η°ΑεΫïεΚèεà½Xi壨Yjγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½γö³ιïΩεΚΠψIJεÖΕδΗ≠Xi=<x1, x2, …, xi>εQ¨Yj=<y1, y2, …, yj>ψIJεΫ™i=0φà•j=0φ½”ûΦ¨ΫIΚεΚèεà½φ‰·Xi壨Yjγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½εQ¨φïÖc[i,j]=0ψIJεÖΕδΜ•φÉÖεÜΒδΗ΄εQ¨γî±ε°öγêÜεè·εΨèγΪ΄ιÄ£εΫ£εÖ≥γ≥ΜεΠ²δΗ΄εQ?/p>
3.η°Γγ°½φ€ÄδΦ‰εÄ?/h4>
㦥φéΞεà©γî®(2.2)εΦèε°Ιφ‰™εÜôε΅όZΗÄδΗΣη°ΓΫé½c[i,j]γö³ιÄ£εΫ£Ϋé½φ≥ïεQ¨δΫÜεÖΕη°ΓΫé½φ½Ει½¥φ‰·ιöèηΨ™εÖΞιïΩεΚΠφ¨΅φïΑεΔûιïΩγö³ψIJγî±δΚéε€®φâÄηÄÉηôëγö³ε≠êι½°ιΔ‰ΫIΚι½¥δΗ≠οΦ¨φÄ’dÖ±εèΣφ€âθ(m*n)δΗΣδΗçεê¨γö³ε≠êι½°ιΔ‰ο֨妆φ≠ΛεQ¨γî®εä®φĹηß³εà£γ°½φ≥ïη΅ΣεΚïεêëδΗäε€Αη°Γγ°½φ€ÄδΦ‰εÄΤDÉΫφèêιΪ‰Ϋé½φ≥ïγö³φïàγé΅ψÄ?/p>
η°Γγ°½φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ιïΩεΚΠγö³εä®φĹηß³εà£γ°½φ≥ïLCS_LENGTH(X,Y)δΜΞεΚèεà½X=<x1, x2, …, xm>壨Y=<y1, y2, …, yn>δΫ€δΊ™(f®¥)ηΨ™εÖΞψIJηΨ™ε΅όZΗΛδΗΣφïΑΨl³c[0..m ,0..n]壨b[1..m ,1..n]ψIJεÖΕδΗ≠c[i,j]ε≠‰ε²®XiδΗéYjγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½γö³ιïΩεΚΠοΦ¨b[i,j]η°ΑεΫïφ¨΅γΛΚc[i,j]γö³εÄΦφ‰·γî±ε™ΣδΗÄδΗΣε≠êι½°ιΔ‰γö³ηßΘηΨë÷àΑγö³οΦ¨‰qôε€®φû³ιĆφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½φ½ΕηΠ¹γî®εàΑψIJφ€ÄεêéοΦ¨X壨Yγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½γö³ιïΩεΚΠη°ΑεΫïδΚéc[m,n]δΗ≠ψÄ?/p>
Procedure LCS_LENGTH(X,Y);
begin
m:=length[X];
n:=length[Y];
for i:=1 to m do c[i,j]:=0;
for j:=1 to n do c[0,j]:=0;
for i:=1 to m do
for j:=1 to n do
if x[i]=y[j] then
begin
c[i,j]:=c[i-1,j-1]+1;
b[i,j]:="βÜ?;
end
else if c[i-1,j]≥c[i,j-1] then
begin
c[i,j]:=c[i-1,j];
b[i,j]:="↑";
end
else
begin
c[i,j]:=c[i,j-1];
b[i,j]:="←"
end;
return(c,b);
end;
γîΉÉΚéφ·èδΗΣφïΑγΜ³εçïεÖÉγö³η°ΓΫé½ηĽη¥ΙΟ(1)φ½âô½¥εQ¨γ°½φ≥ïLCS_LENGTHηĽφ½ΕΟ(mn)ψÄ?/p>
4.φû³ιĆφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½
γîόq°½φ≥ïLCS_LENGTHη°Γγ°½εΨ½εàΑγö³φïΑΨl³bεè·γî®δΚéεΩΪιÄüφû³ιĆεΚèεà½X=<x1, x2, …, xm>壨Y=<y1, y2, …, yn>γö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψIJιΠ•εÖàδΜéb[m,n]εΦÄεß΄οΦ¨φ≤ΩγùÄεÖΕδΗ≠γö³γ°≠εΛ¥φâÄφ¨΅γö³φ•Ιεêëε€®φïΑΨl³bδΗ≠φê€γ¥ΔψIJεΫ™b[i,j]δΗ≠ι¹΅εà?βÜ?φ½”ûΦ¨ηΓ®γΛΚXiδΗéYjγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½φ‰·γî±Xi-1δΗéYj-1γö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ε€®εΑΨιÉ®εä†δΗäxiεΨ½εàΑγö³ε≠êεΚèεà½εQ¦εΫ™b[i,j]δΗ≠ι¹΅εà?↑"φ½”ûΦ¨ηΓ®γΛΚXiδΗéYjγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ε£¨Xi-1δΗéYjγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½γ¦Ηεê¨εQ¦εΫ™b[i,j]δΗ≠ι¹΅εà?←"φ½”ûΦ¨ηΓ®γΛΚXiδΗéYjγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ε£¨XiδΗéYj-1γö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½γ¦Ηεê¨ψÄ?/p>
δΗ΄ιùΔγö³γ°½φ≥ïLCS(b,X,i,j)ε°ûγéΑφ†“é(gu®©)ç°bγö³εÜÖε°“é(gu®©)â™εçΑε΅ΚXiδΗéYjγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψIJιÄöηΩ΅Ϋé½φ≥ïγö³ηΑÉγî®LCS(b,X,length[X],length[Y])εQ¨δΨΩεè·φâ™εçΑε΅ΚεΚèεà½X壨Yγö³φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½ψÄ?/p>
Procedure LCS(b,X,i,j);
begin
if i=0 or j=0 then return;
if b[i,j]="βÜ? then
begin
LCS(b,X,i-1,j-1);
print(x[i]); {φâ™εçΑx[i]}
end
else if b[i,j]="↑" then LCS(b,X,i-1,j)
else LCS(b,X,i,j-1);
end;
ε€®γ°½φ≥ïLCSδΗ≠οΦ¨φ·èδΗÄ΄ΤΓγö³ιÄ£εΫ£ηΑÉγî®δΫΩiφà•jε΅?εQ¨ε¦†φ≠Λγ°½φ≥ïγö³η°Γγ°½φ½âô½¥δΗ?em>O(m+n)ψÄ?/p>
δΨ΄εΠ²εQ¨η°ΨφâÄΨlôγö³δΗΛδΗΣεΚèεà½δΗΚX=<AεQ¨BεQ¨CεQ¨BεQ¨DεQ¨AεQ¨B>壨Y=<BεQ¨DεQ¨CεQ¨AεQ¨BεQ¨A>ψIJγî±Ϋé½φ≥ïLCS_LENGTH壨LCSη°Γγ°½ε΅Κγö³Ψl™φû€εΠ²ε¦Ψ2φâÄΫCΚψÄ?/p>
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | |||||||||
| i | yj | B | D | C | A | B | A | |||||||||
| βî?/td> | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βî?/td> | ||
| 0 | xi | βî?/td> | 0 | 0 | 0 | 0 | 0 | 0 | βî?/td> | |||||||
| βî?/td> | ↑ | ↑ | ↑ | βÜ?/td> | βÜ?/td> | βî?/td> | ||||||||||
| 1 | A | βî?/td> | 0 | 0 | 0 | 0 | 1 | ← | 1 | 1 | βî?/td> | |||||
| βî?/td> | βÜ?/td> | ↑ | βÜ?/td> | βî?/td> | ||||||||||||
| 2 | B | βî?/td> | 0 | 1 | ← | 1 | ← | 1 | 1 | 2 | ← | 2 | βî?/td> | |||
| βî?/td> | ↑ | ↑ | βÜ?/td> | ↑ | ↑ | βî?/td> | ||||||||||
| 3 | C | βî?/td> | 0 | 1 | 1 | 2 | ← | 2 | 2 | 2 | βî?/td> | |||||
| βî?/td> | βÜ?/td> | ↑ | ↑ | ↑ | βÜ?/td> | βî?/td> | ||||||||||
| 4 | B | βî?/td> | 0 | 1 | 1 | 2 | 2 | 3 | ← | 3 | βî?/td> | |||||
| βî?/td> | ↑ | βÜ?/td> | ↑ | ↑ | ↑ | ↑ | βî?/td> | |||||||||
| 5 | D | βî?/td> | 0 | 1 | 2 | 2 | 2 | 3 | 3 | βî?/td> | ||||||
| βî?/td> | ↑ | ↑ | ↑ | βÜ?/td> | ↑ | βÜ?/td> | βî?/td> | |||||||||
| 6 | A | βî?/td> | 0 | 1 | 2 | 2 | 3 | 3 | 4 | βî?/td> | ||||||
| βî?/td> | βÜ?/td> | ↑ | ↑ | ↑ | βÜ?/td> | ↑ | βî?/td> | |||||||||
| 7 | B | βî?/td> | 0 | 1 | 2 | 2 | 3 | 4 | 5 | βî?/td> | ||||||
| βî?/td> | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βîÄ | βî?/td> |
ε¦? Ϋé½φ≥ïLCSγö³η°ΓΫé½γΜ™φû?/font>
5.Ϋé½φ≥ïγö³φîΙ‰q?/h4>
ε·ΙδΚéδΗÄδΗΣεÖΖδΫ™ι½°ιΔ‰οΦ¨φ¨âγÖßδΗÄηà§γö³Ϋé½φ≥ïη°Ψη°ΓΫ{•γïΞη°Ψη°Γε΅Κγö³Ϋé½φ≥ïεQ¨εΨÄεΨÄε€®γ°½φ≥ïγö³φ½âô½¥ε£¨γ©Κι½¥ι€Äφ±²δΗä‰q‰εè·δΜΞφîΙ‰q¦ψIJηΩôΩUçφîΙ‰q¦οΦ¨ιÄöεΗΗφ‰·εà©γî®εÖΖδΫ™ι½°ιΔ‰γö³δΗÄδΚ¦γâΙ¨DäφÄßψÄ?/p>
δΨ΄εΠ²εQ¨ε€®Ϋé½φ≥ïLCS_LENGTH壨LCSδΗ≠οΦ¨εè·ηΩ¦δΗÄφ≠ΞεΑÜφïΑγΜ³bγ€¹εéΜψIJδΚ΄ε°ûδΗäεQ¨φïΑΨl³εÖÉ㥆c[i,j]γö³εÄιgΜÖγî±c[i-1,j-1]εQ¨c[i-1, j]壨c[i,j-1]δΗâδΗΣεÄιgΙ΄δΗÄΦ΄°ε°öεQ¨ηĨφïΑΨl³εÖÉ㥆b[i,j]δΙüεèΣφ‰·γî®φùΞφ¨΅ΫCΚc[i,j]ΫIΕγΪüγî±ε™ΣδΗΣεÄΦγΓ°ε°öψÄ²ε¦†φ≠ΛοΦ¨ε€®γ°½φ≥ïLCSδΗ≠οΦ¨φàëδΜ§εè·δΜΞδΗçεÄüεä©δΚéφïΑ Ψl³bηĨεÄüεä©δΚéφïΑΨl³cφ€§ημnδΗ¥φ½ΕεàΛφ•≠c[i,j]γö³εÄΦφ‰·γî±c[i-1,j-1]εQ¨c[i-1,j]壨c[i,j-1]δΗ≠ε™ΣδΗÄδΗΣφïΑεÄΦεÖÉ㥆φâÄΦ΄°ε°öεQ¨δΜΘδΜδh‰·Ο(1)φ½âô½¥ψIJφ½Δγ³Εbε·ΙδΚéΫé½φ≥ïLCSδΗçφ‰·εΩÖηΠ¹γö³οΦ¨ι²ΘδΙàΫé½φ≥ïLCS_LENGTHδΨΩδΗçεΩÖδΩùε≠‰ε°ÉψIJηΩôδΗÄφùΞοΦ¨εè·ηä²γ€?em>θ(mn)γö³γ©Κι½Ώ_(d®Δ)Φ¨ηĨLCS_LENGTH壨LCSφâÄι€ÄηΠ¹γö³φ½âô½¥εàÜεàΪδΜçγ³Εφ‰?em>Ο(mn)ε£?em>Ο(m+n)ψIJδΗç‰q΅οΦ¨γîΉÉΚéφïΑγΜ³cδΜçι€ÄηΠ?em>Ο(mn)γö³γ©Κι½Ώ_(d®Δ)֨妆φ≠Λ‰qô顨φâÄδΫ€γö³φîΙηΩ¦εQ¨εèΣφ‰·ε€®ΫIΚι½¥εΛçφù²φÄßγö³εΗΗφïΑ妆ε≠êδΗäγö³φîΙηΩ¦ψÄ?/p>
εèΠεΛ•εQ¨εΠ²φû€εèΣι€ÄηΠ¹η°ΓΫé½φ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½γö³ιïΩεΚΠοΦ¨εàôγ°½φ≥ïγö³ΫIΚι½¥ι€Äφ±²ηΩ‰εè·εΛßεΛßε΅èû°ëψIJδΚ΄ε°ûδΗäεQ¨ε€®η°Γγ°½c[i,j]φ½”ûΦ¨εèΣγî®εàΑφïΑΨl³cγö³γ§§iηè壨ΫW§i-1ηΓ¨ψÄ²ε¦†φ≠ΛοΦ¨εèΣηΠ¹γî?ηΓ¨γö³φïΑγΜ³ΫIΚι½¥û°±εè·δΜΞη°ΓΫé½ε΅Κφ€ÄιïΩεÖ§εÖ±ε≠êεΚèεà½γö³ιïΩεΚΠψIJφ¦¥‰q¦δΗÄφ≠Ξγö³εàÜφûê‰q‰εè·û°Üγ©Κι½¥ι€Äφ±²ε΅èη΅≥min(m, n)ψÄ?/p>









