一、同?/p>
我们来了(jin)解一下什么是“同余”。简单来说就是，如果两个数都除以某个数能够有相同的余敎ͼ那么我们pq两个数“同余”。不q这ơ我们用严}的数学概忉|表述Q?/p>
两个整数 aQ?em>bQ若它们除以整数 m 所得的余数相等Q则U?aQ?em>b 对于?m 同余
C 
M a 同余?b ?m Q或M a ?b 关于?m 同余?/p>
比如 
我们再来?jin)解一下相关的性质Q?/p>
- 如果 Q那?m | (a − b) Q这?m | (a − b) 表示 (a − b) 能被 m 整除
- 如果 Q?img alt="b " src="http://upload.wikimedia.org/math/7/2/c/72c4fa0bd69956b7e68d3d8cc2ec9d5c.png" />, 那么
- 如果 Q?img alt="c " src="http://upload.wikimedia.org/math/7/7/b/77b3768cf453ddc62ff2c3e668b93fad.png" />, 那么
Q?img alt="a-c " src="http://upload.wikimedia.org/math/9/e/f/9ef96c57e3ad5d862af3178c718177d6.png" />Q?img alt="ac " src="http://upload.wikimedia.org/math/3/9/0/390116f8d52af94ccdb17c5ad2e199c0.png" />Q?img alt="a/c " src="http://upload.wikimedia.org/math/f/9/e/f9e3c5a2ad4272a6b596a641cb3bdb21.png" /> - 如果 Q?那么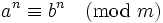
有了(jin)q些性质Q判断两个数是否同余可以用更简单的Ҏ(gu)?jin)。根据性质一Q原来我们需要判?(a mod m) == (b mod m) 是否为真Q现在就可以直接判断 (a - b) mod m == 0 是否为真?jin)。这样就把其中一ơ求余运变?sh)减法运?jin)。一般来说减法要比除法更Ҏ(gu)在计机上实玎ͼq算速度也更快?/p>
二、求?(a * b * c * d) mod m = ?
׃计算CZ个整数通常?32bit 。而大量连乘运则可能?x)导致整数溢出，q时我们p利用求余一些性质来进行处理了(jin)。把以上式子转换为：(x)
已知Q?(a * b) mod m == ((a mod m) * b) mod m
所以：(x) (a * b * c * d) mod m = ((((((a mod m) * b) mod m) * c) mod m) * d) mod m
q样把q乘q算分解?jin)，每次可以先进行求余运然后再q行乘法q算?/p>
在网上找?jin)点资料Q在ibus已经加入到Ubuntu的源?jin)，如果需要，使用下面的命令进行安装：(x)
- sudo apt-get update 更新软g包列?/li>
- sudo apt-get install ibus 安装ibus框架
- sudo apt-get install ibus ibus-table 安装某些输入法引擎基Q如果仅仅想使用拼音输入法，可以跌此步Q拼韌入法不需要依赖ibus-table。某些输入法Q如五笔Q依赖ibus-table?/li>
- sudo apt-get install ibus ibus-pinyin 安装拼音输入法引擎，发现很好用啊Q哈?/li>
׃安装和卸载Y件是使用的必d提，所以这里对apt命o(h)q行一些ȝ。在ȝ之前Q还得对ubuntu的Y件源的地址q行说明Qؓ(f)?jin)达到好的下载源的速度Q最好选一个最快的软g源，目前来说http://ubuntu.srt.cn是最快的Qubuntu自己提供?jin)检的功能Q可以自动检（choose a download server -> select best serverQ?/p>
关于apt-get命o(h)的详l而简单的说明Q是?a >AptGetHowTo》。注意，使用apt-get命o(h)必须要用root权限。这里，摘抄?jin)最常用的命?...如下
Installation commands
apt-get install <package_name>
This command installs a new package.apt-get build-dep <package_name>
This command searches the repositories and installs the build dependencies for <package_name>. If the package is not in the repositories it will return an error.
aptitude install <package_name>
Aptitude is a [http://en.wikipedia.org/wiki/Ncurses Ncurses] viewer of packages installed or available. Aptitude can be used from the command line in a similar way to apt-get. See man aptitude for more information.
- APT and aptitude will accept multiple package names as a space delimited list. For example:
apt-get install <package1_name> <package2_name> <package3_nam
Search commands
apt-cache search <search_term>
This command will find packages that include <search_term>.
dpkg -l *<search_term>*
This will find packages whose names contain <search_term>. Similar to apt-cache search, but also shows whether a package is installed on your system by marking it with ii (installed) and un (not installed).
apt-cache show <package_name>
This command shows the description of package <package_name> and other relevant information including version, size, dependencies and conflicts.
Typical usage example
I want to feel the wind in my hair, I want the adrenaline of speed. So lets install a racing game. But what racing games are available?
apt-cache search racing game
It gives me a lot of answers. I see a game named "torcs". Lets get some more information on this game.
apt-cache show torcs
Hmmm... it seems interesting. But is this game not already installed on my computer? And what is the available version? Is it from Universe or main?
apt-cache policy torcs
Ok, so now, let's install it!
apt-get install torcs
What is the command I must type in the console to launch this game? In this example, it's straightforward ("torcs"), but that's not always the case. One way of finding the name of the binary is to look at what files the package has installed in "/usr/bin". For games, the binary will be in "/usr/games". For administrative programs, it's in "/usr/sbin".
dpkg -L torcs | grep /usr/games/
The first part of the command display all files installed by the package "torcs" (try it). With the second part, we ask to only display lines containing "/usr/games/".
Hmmm, that game is cool. Maybe there are some extra tracks?
apt-cache search torcs
But I'm running out of space. I will delete the apt cache!
apt-get clean
Oh no, my mother asked me to remove all games from this computer. But I want to keep the configuration files so I can simply re-install it later.
apt-get remove torcs
If I want to also remove config files :
apt-get purge torcs
文章来源:http://localhost/wp2/?p=180
转自 http://alexmogurenko.com/blog/programming/android-how-to-set-proxy-for-android-browser/
下面是原?/p>
There are many reasons to make browser serf pages through proxy server:
- someone wanna catch http requests/responses
- someone wanna hide his IP
- so on
What to do if you want set proxy for android browser? there some ways:
- add record to database: /data/data/com.android.providers.settings/databases/settings.db
- pull database to pc add record (using for example sdk tool sqlite3) and replace existing db
- make changes in database directly on device
but as for me there exist simplier way, do it by your Java application using Settings provider:
Settings.System.putString(getContentResolver(), Settings.System.HTTP_PROXY, "proxy_ip:proxy_port");
where proxy_ip/proxy_port = IP/port of proxy that you going to use.
there left one problem, it will not work if we will not add one string to manifest file, here it is:
<uses-permission android:name=”android.permission.WRITE_SETTINGS” />
Thats all, now it works, here is code:
package com.BrowserSettings;
import android.app.Activity;
import android.os.Bundle;
import android.view.View;
import android.widget.Button;
import android.provider.Settings;
public class BrowserSettingsUI extends Activity {
/** Called when the activity is first created. */
@Override
public void onCreate(Bundle savedInstanceState) {
super.onCreate(savedInstanceState);
setContentView(R.layout.main);
final Button button = (Button) findViewById(R.id.Button01);
button.setOnClickListener(new Button.OnClickListener() {
public void onClick(View v) {
try
{
Settings.System.putString(getContentResolver(), Settings.System.HTTP_PROXY, "127.0.0.1:100");//enable proxy
}catch (Exception ex){
}
}
});
final Button button2 = (Button) findViewById(R.id.Button02);
button2.setOnClickListener(new Button.OnClickListener() {
public void onClick(View v) {
try
{
Settings.System.putString(getContentResolver(), Settings.System.HTTP_PROXY, "");//disable proxy
}catch (Exception ex){
}
}
});
}
}
manifest file:
<?xml version=”1.0″ encoding=”utf-8″?>
<manifest xmlns:android=”http://schemas.android.com/apk/res/android”
package=”com.BrowserSettings”
android:versionCode=”1″
android:versionName=”1.0.0″>
<application android:icon=”@drawable/icon” android:label=”@string/app_name”>
<activity android:name=”.BrowserSettingsUI”
android:label=”@string/app_name”>
<intent-filter>
<action android:name=”android.intent.action.MAIN” />
<category android:name=”android.intent.category.LAUNCHER” />
</intent-filter>
</activity>
</application>
<uses-permission android:name=”android.permission.WRITE_SETTINGS” />
</manifest>
文章来源:http://localhost/wp2/?p=172
数学归纳法用来在数学上证明与自然?/b>N有关的命题的一U特D方法，它主要用来研I与正整?/b>有关的数学问题，在高?sh)数学中常用来证明等式成立和数列通项公式成立?/p>
用的最多的是第一数学归纳法和W二数学归纳法，下面详细说明?/p>
W一数学归纳?br />
- 证明当nQn然数Q?/strong>取第一个值时命题成立
- 假设当n=kQ?b>k然数Q时命题成立Q证明当n=k+1时命题(sh)成立
?Q?步，可证明命题成立?/p>
W二数学归纳?br />
对第一数学归纳法进行了(jin)扩充
- 证明当n=0时命题成?/li>
- 假设当n<=kQ?b>k然数Q时命题成立Q证明当n=k+1时命题(sh)成立
?Q?步，可证明命题成立?/p>
在算法时间复杂度的证明上Q由于n取值是一个自然数Q所以多用数学归Ux(chng)原理q行证明。其实，证明循环正确性的循环不变式就是直接利用的W一数学归纳法?/p>
参考：(x)
癑ֺ癄Q数学归Ux(chng)
文章来源:http://localhost/wp2/?p=165
递归实现
思\Q如果只有一个节点，则什么都不做。否则，当前链表（a1,a2...a3Q的子链表（a2,...anQ进行逆{Q返回逆{后的W一个节点的指针Q再a1节点加到a2节点后面?/p>
代码Q?q里没有使用头节?
node * reverse(node * p){
if(p->next == null){
return p;
}
node * q = p->next;
node * head = reverse(q);
p->next = null;
q->next = p;
return head;
}
非递归实现
思\Q一个指针进行链表的遍历Q一个指针指向逆{后的链表的第一个节点，在遍历的q程中，当前节点加入逆{后的链表W一个元素即可。返回逆{后的链表的第一个节点的指针?/p>
代码Q（q里没有使用头节点）(j)
node * reverse(node * p){
node * p_reverse;
if(p != null){
p_reverse = p;
node * q = p->next;
p->next = null;
}
while(q != null){
p = q->next;
q->next = p_reverse;
p_reverse = q;
q = p;
}
}
对C语言用的太少Q上面的代码实现可能有点恶心(j)Q不q可以实现功?...
文章来源:http://localhost/wp2/?p=150
以前安装Eclipse插g无非两种方式, 直接copy插g到features/plugins目录或者在links目录下创建链接文? 刚刚发布的Eclipse 3.4又推出另一U新的安装途径, 更加灉|。Eclipse 3.4下有个dropins目录, 只要把插件放到该目录下就可以加蝲, 有几U格式可以选择?/p>
1. 最单的Q直接将jar包放到dropins目录:
eclipse/
dropins/
com.essiembre.eclipse.i18n.resourcebundle_0.7.7
2. 传统格式Q统一攑ֈ一个eclipse目录?
eclipse/
dropins/
eclipse/
features/
plugins/
3. 按照插g名称区分:
eclipse/
dropins/
resourcebundleeditor/
features/
plugins/
m2eclipse/
features/
plugins/
4. cMlinks方式d链接:
eclipse/
dropins/
xfire.link
如果只安装一个Eclipse的话采用W三U，否则采用W四U?/p>
如果发现安装?jin)没有效果，可以删除eclipseȝ录下的\configuration\org.eclipse.update后，再执行eclipse -clean试试?/p>
文章来源:http://localhost/wp2/?p=127
字符数据cd
CHAR数据cd存储固定长度的字W倹{一个CHAR数据cd可以包括1?000个字W。如果对CHAR没有明确地说明长度，它的默认长度则设|ؓ(f)1.如果Ҏ(gu)个CHARcd变量赋|光度小于规定的长度Q那么Oracle自动用空格填充?/p>
VARCHAR2存储可变长度的字W串。虽然也必须指定一个VARCHAR2数据变量的长度，但是q个长度是指对该变量赋值的的最大长度而非实际赋值长度。不需要用I格填充。最多可讄?000个字节。所以如果存储中文的时候，׃能存储到4000个字W了(jin)Q因Z个汉字会(x)占有多个字节?/p>
因ؓ(f)VARCHAR2数据cd只存储ؓ(f)该列所赋的字符Q不加空|(j)Q所以VARCHAR2需要的存储I间比CHAR数据cd要小?/p>
Oracle推荐使用VARCHAR2
NCHAR和NVARCHAR2数据cd分别存储固定长度与可变长度的字符数据Q但是它们用的是和数据库其他类型不同的字符集。在创徏数据库时Q需要指定所使用的字W集Q以便对数据库中数据q行~码。还可以指定一个辅助的字符集Ex(chng)地语a集（National Language SetQ简UNLSQ］。NCHAR和NVARCHAR2cd的列使用辅助字符集?/p>
在Oracle9i中，可以以字W而不是字节ؓ(f)单位来表CNCHAR和NVARCHAR2列的长度?/p>
LONG数据cd可以存放2GB的字W数据，它是从早期版本中l承来的。现在如果想存储大容量的数据QOracle推荐使用CLOB和NCLOB数据cd。在表和SQL语句中用LONGcd有许多限制?/p>
CLOB和NCLOB数据cd可以存储多达4GB的字W数据。NCLOB数据cd可存储NLS数据?/p>
数字数据cd
Oracle使用标准、可变长度的内部格式来存储数字。这个内部格式精度可以高?8位?/p>
NUMBER数据cd可以有两个限定符Q如Q?/p>
column NUMBER Q?precisionQ?scaleQ?/p>
precision表示数字中的有效位。如果没有指定precision的话QOracle?8作ؓ(f)_ֺ?/p>
scale表示数字数点右边的位数Qscale默认讄?。如果把scale设成负数QOracle把该数字取舍到数点左边的指定位数?/p>
日期数据cd
Oracle标准日期格式为：(x)DD-MON-YY HHQMIQSS
通过修改实例的参数NLS_DATE_FORMATQ可以改变实例中插入日期的格式。在一个会(x)话期_(d)可以通过ALTER SESSION SQL命o(h)来修Ҏ(gu)期，或者通过使用SQL语句的TO_DATE表达式中的参数来更新一个特定倹{?/p>
其它的数据类?/p>
RAW和LONG RAW数据cd主要用于Ҏ(gu)据库q行解释。指定这两种cdӞOracle以位的Ş式来存储数据。RAW数据cd一般用于存储有特定格式的对象，如位图?RAW数据cd可占?KB的空_(d)而LONG RAW数据cd则可以占?GB大小?/p>
ROWID ROWID是一U特D的列类型，UCZ列（pseudocolumnQ。ROWID伪列在SQL SELECT语句中可以像普通列那样被访问。Oracle数据库中每行都有一个伪列。ROWID表示行的地址QROWID伪列用ROWID数据cd定义?/p>
ROWID与磁盘驱动的特定位置有关Q因此，ROWID是获得行的最快方法。但是，行的ROWID?x)随着卸蝲和重载数据库而发生变化，因此不要在事?中用ROWID伪列的倹{例如，一旦当前应用已l用完记录Q就没有理由保存行的ROWID.不能通过MSQL语句来设|标准的ROWID伪列的倹{?/p>
列或变量可以定义成ROWID数据cdQ但是Oracle不能保证该列或变量的值是一个有效的ROWID.
LOB
LOBQ大型对象）(j)数据cdQ可以保?GB的信息。LOB有以?U类型：(x)
。CLOBQ只能存储字W数?/p>
。NCLOBQ保存本地语a字符集数?/p>
。BLOBQ以二进制信息保存数?/p>
可以指定一个LOB数据保存在Oracle数据库内Q还是指向一个包含次数据的外部文件?/p>
LOB可以参与事务。管理LOB中的数据必须通过DBMS_LOB PL/SQL内置软g包或者OCI接口?/p>
Z(jin)便于LONG数据cd转换成LOBQOracle9i包含许多同时支持LOB和LONG的函敎ͼq包括一个ALTER TABLE语句的的新选择Q它允许LONG数据cd自动转换成LOB.
BFILE
BFILE数据cd用做指向存储在Oracle数据库以外的文g的指针?/p>
XMLType
作ؓ(f)对XML支持的一部分QOracle9i包含?jin)一个新的数据类型XMLType.定义为XMLType的列存储一个在字符LOB列中的XML文档。有许多内置的功能可以你从文当中抽取单个节点，q可以在XMLType文档中对M节点创徏索引?/p>
用户自定义数?/strong>
从Oracle8以后Q用户可以定义自q复杂数据cdQ它们由O(jin)racle基本数据cdl合而成?/p>
AnyType、AnyData和AnyDataSet
Oracle包括3个新的数据类型，用于定义在现有数据类型之外的数据l构。其中每U数据类型必ȝE序单元来定义，以便让Oracle9i知道如何处理q些cd的特定实现?/p>
额外的：(x)
cd转换
Oracle?x)自动将某些数据cd转换成其他的数据cdQ{换取决于包括该值的SQL语句?/p>
数据转换q可以通过Oracle的类型{换函数显C地q行?/p>
q接与比?/strong>
在大多数q_上Oracle SQL中的q接操作W用两条竖线Q||Q表C。连接是两个字WD接。Oracle的自动类型{换功能得两个数字g可以q行q接?/p>
NULL
NULL值是关系数据库的重要特征之一。实际上QNULL不代表Q何|它表C没有倹{如果要创徏表的一个列Q而这个列必须有|那么应将它指定ؓ(f)NOT NULLQ这表示该列不能包含NULL倹{?/p>
M数据cd都可以赋予NULL倹{NULL值引入了(jin)SQLq算的三态逻辑。如果比较的一Ҏ(gu)NULL|那么?x)出?U状态：(x)TURE、FALSE以及(qing)两者都不是?/p>
因ؓ(f)NULLg{于0或其他Q何|所以测试某个数据是否ؓ(f)NULL值只能通过关系q算WIS NULL来进行?/p>
NULL值特别适合以下情况Q当一个列q未赋值时。如果选择不用NULL|那么必须对行的所有列都要赋倹{这实际上也取消?jin)某列不需要值的可能性，同时对它赋的g很容易生误解。这U情况则可能误导l端用户Qƈ且导致篏计操作的错误l果?/p>
参考：(x)
《Oracle数据cd》，http://www.cnblogs.com/cxd4321/archive/2008/04/14/1153201.html
文章来源:http://localhost/wp2/?p=122
- java.lang.Objectc（?qing)其子类Q实例的waitҎ(gu)
- java.lang.Objectc（?qing)其子类Q实例的sleepҎ(gu)
- java.lang.Threadc（?qing)其子类Q实例的joinҎ(gu)
文章来源:http://localhost/wp2/?p=99