consistent hashing 綆楁硶鏃╁湪 1997 騫村氨鍦ㄨ鏂?/span> Consistent hashing and random trees 涓鎻愬嚭錛岀洰鍓嶅湪 cache 緋葷粺涓簲鐢ㄨ秺鏉ヨ秺騫挎硾錛?/span>
1 鍩烘湰鍦烘櫙
姣斿浣犳湁 N 涓?/span> cache 鏈嶅姟鍣紙鍚庨潰綆縐?/span> cache 錛夛紝閭ｄ箞濡備綍灝嗕竴涓璞?/span> object 鏄犲皠鍒?/span> N 涓?/span> cache 涓婂憿錛屼綘寰堝彲鑳戒細(xì)閲囩敤綾諱技涓嬮潰鐨勯氱敤鏂規(guī)硶璁＄畻 object 鐨?/span> hash 鍊鹼紝鐒跺悗鍧囧寑鐨勬槧灝勫埌鍒?/span> N 涓?/span> cache 錛?/span>
hash(object)%N
涓鍒囬兘榪愯姝ｅ父錛屽啀鑰冭檻濡備笅鐨勪袱縐嶆儏鍐碉紱
1 涓涓?/span> cache 鏈嶅姟鍣?/span> m down 鎺変簡(jiǎn)錛堝湪瀹為檯搴旂敤涓繀欏昏鑰冭檻榪欑鎯呭喌錛夛紝榪欐牱鎵鏈夋槧灝勫埌 cache m 鐨勫璞￠兘浼?xì)澶辨晥锛屾庝箞鍔烇紝闇瑕佹妸 cache m 浠?/span> cache 涓Щ闄わ紝榪欐椂鍊?/span> cache 鏄?/span> N-1 鍙幫紝鏄犲皠鍏紡鍙樻垚浜?/span> hash(object)%(N-1) 錛?/span>
2 鐢變簬璁塊棶鍔犻噸錛岄渶瑕佹坊鍔?/span> cache 錛岃繖鏃跺?/span> cache 鏄?/span> N+1 鍙幫紝鏄犲皠鍏紡鍙樻垚浜?/span> hash(object)%(N+1) 錛?/span>
1 鍜?/span> 2 鎰忓懗鐫浠涔堬紵榪欐剰鍛崇潃紿佺劧涔嬮棿鍑犱箮鎵鏈夌殑 cache 閮藉け鏁堜簡(jiǎn)銆傚浜庢湇鍔″櫒鑰岃█錛岃繖鏄竴鍦虹伨闅撅紝媧按鑸殑璁塊棶閮戒細(xì)鐩存帴鍐插悜鍚庡彴鏈嶅姟鍣紱
鍐嶆潵鑰冭檻絎笁涓棶棰橈紝鐢變簬紜歡鑳藉姏瓚婃潵瓚婂己錛屼綘鍙兘鎯寵鍚庨潰娣誨姞鐨勮妭鐐瑰鍋氱偣媧伙紝鏄劇劧涓婇潰鐨?/span> hash 綆楁硶涔熷仛涓嶅埌銆?/span>
鏈変粈涔堟柟娉曞彲浠ユ敼鍙樿繖涓姸鍐靛憿錛岃繖灝辨槸 consistent hashing...
2 hash 綆楁硶鍜屽崟璋冩?/h2>
銆銆 Hash 綆楁硶鐨勪竴涓 閲忔寚鏍囨槸鍗曡皟鎬э紙 Monotonicity 錛夛紝瀹氫箟濡備笅錛?/span>
銆銆鍗曡皟鎬ф槸鎸囧鏋滃凡緇忔湁涓浜涘唴瀹歸氳繃鍝堝笇鍒嗘淳鍒頒簡(jiǎn)鐩稿簲鐨勭紦鍐蹭腑錛屽張鏈夋柊鐨勭紦鍐插姞鍏ュ埌緋葷粺涓傚搱甯岀殑緇撴灉搴旇兘澶熶繚璇佸師鏈夊凡鍒嗛厤鐨勫唴瀹瑰彲浠ヨ鏄犲皠鍒版柊鐨勭紦鍐蹭腑鍘伙紝鑰屼笉浼?xì)琚槧灏勫埌鏃х殑缂撳啿闆嗗悎涓殑鍏朵粬缂撳啿鍖恒?/span>
瀹規(guī)槗鐪嬪埌錛屼笂闈㈢殑綆鍗?/span> hash 綆楁硶 hash(object)%N 闅句互婊¤凍鍗曡皟鎬ц姹傘?/span>
3 consistent hashing 綆楁硶鐨勫師鐞?/h2>
consistent hashing 鏄竴縐?/span> hash 綆楁硶錛岀畝鍗曠殑璇達(dá)紝鍦ㄧЩ闄?/span> / 娣誨姞涓涓?/span> cache 鏃訛紝瀹冭兘澶熷敖鍙兘灝忕殑鏀瑰彉宸插瓨鍦?/span> key 鏄犲皠鍏崇郴錛屽敖鍙兘鐨勬弧瓚沖崟璋冩х殑瑕佹眰銆?/span>
涓嬮潰灝辨潵鎸夌収 5 涓楠ょ畝鍗曡璁?/span> consistent hashing 綆楁硶鐨勫熀鏈師鐞嗐?/span>
3.1 鐜艦hash 絀洪棿
鑰冭檻閫氬父鐨?/span> hash 綆楁硶閮芥槸灝?/span> value 鏄犲皠鍒頒竴涓?/span> 32 涓虹殑 key 鍊鹼紝涔熷嵆鏄?/span> 0~2^32-1 嬈℃柟鐨勬暟鍊肩┖闂達(dá)紱鎴戜滑鍙互灝嗚繖涓┖闂存兂璞℃垚涓涓錛?/span> 0 錛夊熬錛?/span> 2^32-1 錛夌浉鎺ョ殑鍦嗙幆錛屽涓嬮潰鍥?/span> 1 鎵紺虹殑閭ｆ牱銆?/span>
鍥?/span> 1 鐜艦 hash 絀洪棿
3.2 鎶婂璞℃槧灝勫埌hash 絀洪棿
鎺ヤ笅鏉ヨ冭檻 4 涓璞?/span> object1~object4 錛岄氳繃 hash 鍑芥暟璁＄畻鍑虹殑 hash 鍊?/span> key 鍦ㄧ幆涓婄殑鍒嗗竷濡傚浘 2 鎵紺恒?/span>
hash(object1) = key1;
… …
hash(object4) = key4;
鍥?/span> 2 4 涓璞＄殑 key 鍊煎垎甯?/span>
3.3 鎶奵ache 鏄犲皠鍒癶ash 絀洪棿
Consistent hashing 鐨勫熀鏈濇兂灝辨槸灝嗗璞″拰 cache 閮芥槧灝勫埌鍚屼竴涓?/span> hash 鏁板肩┖闂翠腑錛屽茍涓斾嬌鐢ㄧ浉鍚岀殑hash 綆楁硶銆?/span>
鍋囪褰撳墠鏈?/span> A,B 鍜?/span> C 鍏?/span> 3 鍙?/span> cache 錛岄偅涔堝叾鏄犲皠緇撴灉灝嗗鍥?/span> 3 鎵紺猴紝浠栦滑鍦?/span> hash 絀洪棿涓紝浠ュ搴旂殑 hash鍊兼帓鍒椼?/span>
hash(cache A) = key A;
… …
hash(cache C) = key C;
鍥?/span> 3 cache 鍜屽璞＄殑 key 鍊煎垎甯?/span>
璇村埌榪欓噷錛岄『渚挎彁涓涓?/span> cache 鐨?/span> hash 璁＄畻錛屼竴鑸殑鏂規(guī)硶鍙互浣跨敤 cache 鏈哄櫒鐨?/span> IP 鍦板潃鎴栬呮満鍣ㄥ悕浣滀負(fù)hash 杈撳叆銆?/span>
3.4 鎶婂璞℃槧灝勫埌cache
鐜板湪 cache 鍜屽璞￠兘宸茬粡閫氳繃鍚屼竴涓?/span> hash 綆楁硶鏄犲皠鍒?/span> hash 鏁板肩┖闂翠腑浜?jiǎn)锛屾帴涓嬫潵瑕佽冭檻鐨勫氨鏄浣曞皢瀵硅薄鏄犲皠鍒?/span> cache 涓婇潰浜?jiǎn)銆?/span>
鍦ㄨ繖涓幆褰㈢┖闂翠腑錛屽鏋滄部鐫欏烘椂閽堟柟鍚戜粠瀵硅薄鐨?/span> key 鍊煎嚭鍙戯紝鐩村埌閬囪涓涓?/span> cache 錛岄偅涔堝氨灝嗚瀵硅薄瀛樺偍鍦ㄨ繖涓?/span> cache 涓婏紝鍥犱負(fù)瀵硅薄鍜?/span> cache 鐨?/span> hash 鍊兼槸鍥哄畾鐨勶紝鍥犳榪欎釜 cache 蹇呯劧鏄敮涓鍜岀‘瀹氱殑銆傝繖鏍蜂笉灝辨壘鍒頒簡(jiǎn)瀵硅薄鍜?/span> cache 鐨勬槧灝勬柟娉曚簡(jiǎn)鍚楋紵錛?/span>
渚濈劧緇х畫(huà)涓婇潰鐨勪緥瀛愶紙鍙傝鍥?/span> 3 錛夛紝閭ｄ箞鏍規(guī)嵁涓婇潰鐨勬柟娉曪紝瀵硅薄 object1 灝嗚瀛樺偍鍒?/span> cache A 涓婏紱 object2鍜?/span> object3 瀵瑰簲鍒?/span> cache C 錛?/span> object4 瀵瑰簲鍒?/span> cache B 錛?/span>
3.5 鑰冨療cache 鐨勫彉鍔?/h3>
鍓嶉潰璁茶繃錛岄氳繃 hash 鐒跺悗姹備綑鐨勬柟娉曞甫鏉ョ殑鏈澶ч棶棰樺氨鍦ㄤ簬涓嶈兘婊¤凍鍗曡皟鎬э紝褰?/span> cache 鏈夋墍鍙樺姩鏃訛紝cache 浼?xì)澶辨晥锛寴q涜屽鍚庡彴鏈嶅姟鍣ㄩ犳垚宸ㄥぇ鐨勫啿鍑伙紝鐜板湪灝辨潵鍒嗘瀽鍒嗘瀽 consistent hashing 綆楁硶銆?/span>
3.5.1 縐婚櫎 cache
鑰冭檻鍋囪 cache B 鎸傛帀浜?jiǎn)锛屾犚?guī)嵁涓婇潰璁插埌鐨勬槧灝勬柟娉曪紝榪欐椂鍙楀獎(jiǎng)鍝嶇殑灝嗕粎鏄偅浜涙部 cache B 閫嗘椂閽堥亶鍘嗙洿鍒頒笅涓涓?/span> cache 錛?/span> cache C 錛変箣闂寸殑瀵硅薄錛屼篃鍗蟲(chóng)槸鏈潵鏄犲皠鍒?/span> cache B 涓婄殑閭ｄ簺瀵硅薄銆?/span>
鍥犳榪欓噷浠呴渶瑕佸彉鍔ㄥ璞?/span> object4 錛屽皢鍏墮噸鏂版槧灝勫埌 cache C 涓婂嵆鍙紱鍙傝鍥?/span> 4 銆?/span>
鍥?/span> 4 Cache B 琚Щ闄ゅ悗鐨?/span> cache 鏄犲皠
3.5.2 娣誨姞 cache
鍐嶈冭檻娣誨姞涓鍙版柊鐨?/span> cache D 鐨勬儏鍐碉紝鍋囪鍦ㄨ繖涓幆褰?/span> hash 絀洪棿涓紝 cache D 琚槧灝勫湪瀵硅薄 object2 鍜?/span>object3 涔嬮棿銆傝繖鏃跺彈褰卞搷鐨勫皢浠呮槸閭ｄ簺娌?/span> cache D 閫嗘椂閽堥亶鍘嗙洿鍒頒笅涓涓?/span> cache 錛?/span> cache B 錛変箣闂寸殑瀵硅薄錛堝畠浠槸涔熸湰鏉ユ槧灝勫埌 cache C 涓婂璞＄殑涓閮ㄥ垎錛夛紝灝嗚繖浜涘璞￠噸鏂版槧灝勫埌 cache D 涓婂嵆鍙?/span>
鍥犳榪欓噷浠呴渶瑕佸彉鍔ㄥ璞?/span> object2 錛屽皢鍏墮噸鏂版槧灝勫埌 cache D 涓婏紱鍙傝鍥?/span> 5 銆?/span>
鍥?/span> 5 娣誨姞 cache D 鍚庣殑鏄犲皠鍏崇郴
4 铏氭嫙鑺傜偣
鑰冮噺 Hash 綆楁硶鐨勫彟涓涓寚鏍囨槸騫寵 鎬?/span> (Balance) 錛屽畾涔夊涓嬶細(xì)
騫寵 鎬?/span>
銆銆騫寵 鎬ф槸鎸囧搱甯岀殑緇撴灉鑳藉灝藉彲鑳藉垎甯冨埌鎵鏈夌殑緙撳啿涓幓錛岃繖鏍峰彲浠ヤ嬌寰楁墍鏈夌殑緙撳啿絀洪棿閮藉緱鍒板埄鐢ㄣ?/span>
hash 綆楁硶騫朵笉鏄繚璇佺粷瀵圭殑騫寵 錛屽鏋?/span> cache 杈冨皯鐨勮瘽錛屽璞″茍涓嶈兘琚潎鍖鐨勬槧灝勫埌 cache 涓婏紝姣斿鍦ㄤ笂闈㈢殑渚嬪瓙涓紝浠呴儴緗?/span> cache A 鍜?/span> cache C 鐨勬儏鍐典笅錛屽湪 4 涓璞′腑錛?/span> cache A 浠呭瓨鍌ㄤ簡(jiǎn) object1 錛岃?/span> cache C 鍒欏瓨鍌ㄤ簡(jiǎn) object2 銆?/span> object3 鍜?/span> object4 錛涘垎甯冩槸寰堜笉鍧囪 鐨勩?/span>
涓轟簡(jiǎn)瑙ｅ喅榪欑鎯呭喌錛?/span> consistent hashing 寮曞叆浜?#8220;铏氭嫙鑺傜偣”鐨勬蹇碉紝瀹冨彲浠ュ涓嬪畾涔夛細(xì)
“铏氭嫙鑺傜偣”錛?/span> virtual node 錛夋槸瀹為檯鑺傜偣鍦?/span> hash 絀洪棿鐨勫鍒跺搧錛?/span> replica 錛夛紝涓瀹為檯涓妭鐐瑰搴斾簡(jiǎn)鑻ュ共涓?#8220;铏氭嫙鑺傜偣”錛岃繖涓搴斾釜鏁頒篃鎴愪負(fù)“澶嶅埗涓暟”錛?#8220;铏氭嫙鑺傜偣”鍦?/span> hash 絀洪棿涓互 hash 鍊兼帓鍒椼?/span>
浠嶄互浠呴儴緗?/span> cache A 鍜?/span> cache C 鐨勬儏鍐典負(fù)渚嬶紝鍦ㄥ浘 4 涓垜浠凡緇忕湅鍒幫紝 cache 鍒嗗竷騫朵笉鍧囧寑銆傜幇鍦ㄦ垜浠紩鍏ヨ櫄鎷熻妭鐐癸紝騫惰緗?#8220;澶嶅埗涓暟”涓?/span> 2 錛岃繖灝辨剰鍛崇潃涓鍏變細(xì)瀛樺湪 4 涓?#8220;铏氭嫙鑺傜偣”錛?/span> cache A1, cache A2 浠ｈ〃浜?/span> cache A 錛?/span> cache C1, cache C2 浠ｈ〃浜?/span> cache C 錛涘亣璁句竴縐嶆瘮杈冪悊鎯崇殑鎯呭喌錛屽弬瑙佸浘 6 銆?/span>
鍥?/span> 6 寮曞叆“铏氭嫙鑺傜偣”鍚庣殑鏄犲皠鍏崇郴
姝ゆ椂錛屽璞″埌“铏氭嫙鑺傜偣”鐨勬槧灝勫叧緋諱負(fù)錛?/span>
objec1->cache A2 錛?/span> objec2->cache A1 錛?/span> objec3->cache C1 錛?/span> objec4->cache C2 錛?/span>
鍥犳瀵硅薄 object1 鍜?/span> object2 閮借鏄犲皠鍒頒簡(jiǎn) cache A 涓婏紝鑰?/span> object3 鍜?/span> object4 鏄犲皠鍒頒簡(jiǎn) cache C 涓婏紱騫寵 鎬ф湁浜?jiǎn)寰堝ぇ鎻愰珮銆?/span>
寮曞叆“铏氭嫙鑺傜偣”鍚庯紝鏄犲皠鍏崇郴灝變粠 { 瀵硅薄 -> 鑺傜偣 } 杞崲鍒頒簡(jiǎn) { 瀵硅薄 -> 铏氭嫙鑺傜偣 } 銆傛煡璇㈢墿浣撴墍鍦?/span> cache鏃剁殑鏄犲皠鍏崇郴濡傚浘 7 鎵紺恒?/span>
鍥?/span> 7 鏌ヨ瀵硅薄鎵鍦?/span> cache
“铏氭嫙鑺傜偣”鐨?/span> hash 璁＄畻鍙互閲囩敤瀵瑰簲鑺傜偣鐨?/span> IP 鍦板潃鍔犳暟瀛楀悗緙鐨勬柟寮忋備緥濡傚亣璁?/span> cache A 鐨?/span> IP 鍦板潃涓?/span>202.168.14.241 銆?/span>
寮曞叆“铏氭嫙鑺傜偣”鍓嶏紝璁＄畻 cache A 鐨?/span> hash 鍊鹼細(xì)
Hash(“202.168.14.241”);
寮曞叆“铏氭嫙鑺傜偣”鍚庯紝璁＄畻“铏氭嫙鑺?#8221;鐐?/span> cache A1 鍜?/span> cache A2 鐨?/span> hash 鍊鹼細(xì)
Hash(“202.168.14.241#1”); // cache A1
Hash(“202.168.14.241#2”); // cache A2
5 灝忕粨
Consistent hashing 鐨勫熀鏈師鐞嗗氨鏄繖浜涳紝鍏蜂綋鐨勫垎甯冩х瓑鐞嗚鍒嗘瀽搴旇鏄緢澶嶆潅鐨勶紝涓嶈繃涓鑸篃鐢ㄤ笉鍒般?/span>
http://weblogs.java.net/blog/2007/11/27/consistent-hashing 涓婇潰鏈変竴涓?/span> java 鐗堟湰鐨勪緥瀛愶紝鍙互鍙傝冦?/span>
http://blog.csdn.net/mayongzhan/archive/2009/06/25/4298834.aspx 杞澆浜?jiǎn)涓涓?/span> PHP 鐗堢殑瀹炵幇浠ｇ爜銆?/span>
http://www.codeproject.com/KB/recipes/lib-conhash.aspx C璇█鐗堟湰
涓浜涘弬鑰冭祫鏂欏湴鍧錛?/span>
http://portal.acm.org/citation.cfm?id=258660
http://en.wikipedia.org/wiki/Consistent_hashing
http://www.spiteful.com/2008/03/17/programmers-toolbox-part-3-consistent-hashing/
http://weblogs.java.net/blog/2007/11/27/consistent-hashing
http://tech.idv2.com/2008/07/24/memcached-004/
http://blog.csdn.net/mayongzhan/archive/2009/06/25/4298834.aspx
]]>
姣忎釜甯栧瓙鍓嶉潰鏈変竴涓悜涓婄殑涓夎褰紝濡傛灉浣犺寰楄繖涓唴瀹瑰緢濂斤紝灝辯偣鍑諱竴涓嬶紝鎶曚笂涓紲ㄣ傛牴鎹緱紲ㄦ暟錛岀郴緇熻嚜鍔ㄧ粺璁″嚭鐑棬鏂囩珷鎺掕姒溿備絾鏄紝騫墮潪寰楃エ鏈澶氱殑鏂囩珷鎺掑湪絎竴浣嶏紝榪樿鑰冭檻鏃墮棿鍥犵礌錛屾柊鏂囩珷搴旇姣旀棫鏂囩珷鏇村鏄撳緱鍒板ソ鐨勬帓鍚嶃?/p>
Hacker News浣跨敤Paul Graham寮鍙戠殑Arc璇█緙栧啓錛屾簮鐮佸彲浠ヤ粠arclanguage.org涓嬭澆銆傚畠鐨勬帓鍚嶇畻娉曟槸榪欐牱瀹炵幇鐨勶細(xì)
灝嗕笂闈㈢殑浠ｇ爜榪樺師涓烘暟瀛﹀叕寮忥細(xì)
鍏朵腑錛?/p>
銆銆P琛ㄧず甯栧瓙鐨勫緱紲ㄦ暟錛屽噺鍘?鏄負(fù)浜?jiǎn)蹇界暐鍙戝笘錆h鐨勬姇紲ㄣ?/p>
銆銆T琛ㄧず璺濈鍙戝笘鐨勬椂闂達(dá)紙鍗曚綅涓哄皬鏃訛級(jí)錛屽姞涓?鏄負(fù)浜?jiǎn)闃叉鏈鏂扮殑甯栧瓙瀵艱嚧鍒嗘瘝榪囧皬錛堜箣鎵浠ラ夋嫨2錛屽彲鑳芥槸鍥犱負(fù)浠庡師濮嬫枃绔犲嚭鐜板湪鍏朵粬緗戠珯錛屽埌杞創(chuàng)鑷矵acker News錛屽鉤鍧囬渶瑕佷袱涓皬鏃訛級(jí)銆?/p>
銆銆G琛ㄧず"閲嶅姏鍥犲瓙"錛坓ravityth power錛夛紝鍗沖皢甯栧瓙鎺掑悕寰(xiàn)涓嬫媺鐨勫姏閲忥紝榛樿鍊間負(fù)1.8錛屽悗鏂囦細(xì)璇︾粏璁ㄨ榪欎釜鍊箋?/p>
浠庤繖涓叕寮忔潵鐪嬶紝鍐沖畾甯栧瓙鎺掑悕鏈変笁涓洜绱狅細(xì)
絎竴涓洜绱犳槸寰楃エ鏁癙銆?/strong>
鍦ㄥ叾浠栨潯浠朵笉鍙樼殑鎯呭喌涓嬶紝寰楃エ瓚婂錛屾帓鍚嶈秺楂樸?/p>
浠?a target="_blank" style="margin: 0px; padding: 0px; list-style-type: none; border: none; color: #112233;">涓婂浘鍙互鐪嬪埌錛屾湁涓変釜鍚屾椂鍙戣〃鐨勫笘瀛愶紝寰楃エ鍒嗗埆涓?00紲ㄣ?0紲ㄥ拰30紲紙鍑?鍚庝負(fù)199銆?9鍜?9錛夛紝鍒嗗埆浠ラ粍鑹層佺傳鑹插拰钃濊壊琛ㄧず銆傚湪浠諱竴涓椂闂寸偣涓婏紝閮芥槸榛勮壊鏇茬嚎鍦ㄦ渶涓婃柟錛岃摑鑹叉洸綰垮湪鏈涓嬫柟銆?/p>
濡傛灉浣犱笉鎯寵"楂樼エ甯栧瓙"涓?浣庣エ甯栧瓙"鐨勫樊璺濊繃澶э紝鍙互鍦ㄥ緱紲ㄦ暟涓婂姞涓涓皬浜?鐨勬寚鏁幫紝姣斿(P-1)^0.8銆?/p>
絎簩涓洜绱犳槸璺濈鍙戝笘鐨勬椂闂碩銆?/strong>
鍦ㄥ叾浠栨潯浠朵笉鍙樼殑鎯呭喌涓嬶紝瓚婃槸鏂板彂琛ㄧ殑甯栧瓙錛屾帓鍚嶈秺楂樸傛垨鑰呰錛屼竴涓笘瀛愮殑鎺掑悕錛屼細(xì)闅忕潃鏃墮棿涓嶆柇涓嬮檷銆?/p>
浠庡墠涓寮犲浘鍙互鐪嬪埌錛岀粡榪?4灝忔椂涔嬪悗錛屾墍鏈夊笘瀛愮殑寰楀垎鍩烘湰涓婇兘灝忎簬1錛岃繖鎰忓懗鐫瀹冧滑閮藉皢璺屽埌鎺掕姒滅殑鏈熬錛屼繚璇佷簡(jiǎn)鎺掑悕鍓嶅垪鐨勯兘灝嗘槸杈冩柊鐨勫唴瀹廣?/p>
絎笁涓洜绱犳槸閲嶅姏鍥犲瓙G銆?/strong>
瀹冪殑鏁板煎ぇ灝忓喅瀹氫簡(jiǎn)鎺掑悕闅忔椂闂翠笅闄嶇殑閫熷害銆?/p>
浠?a target="_blank" style="margin: 0px; padding: 0px; list-style-type: none; border: none; color: #112233;">涓婂浘鍙互鐪嬪埌錛屼笁鏍規(guī)洸綰跨殑鍏朵粬鍙傛暟閮戒竴鏍鳳紝G鐨勫煎垎鍒負(fù)1.5銆?.8鍜?.0銆侴鍊艱秺澶э紝鏇茬嚎瓚婇櫋宄紝鎺掑悕涓嬮檷寰楄秺蹇紝鎰忓懗鐫鎺掕姒滅殑鏇存柊閫熷害瓚婂揩銆?/p>
鐭ラ亾浜?jiǎn)绠楁硶鐨勬瀯鎴愬Q屽氨鍙互璋冩暣鍙傛暟鐨勫鹼紝浠ラ傜敤浣犺嚜宸辯殑搴旂敤紼嬪簭銆?/p>
]]>
銆鎯沖繀鏉ョ湅榪欑瘒鍗氭枃鐨勫悓瀛﹀姹夎濉斿簲璇ヤ笉浼?xì)闄岀敓浜?jiǎn)鍚э紝
銆銆鍐欒繖綃囧崥榪樻槸鏈夊垵琛風(fēng)殑錛?/p>
銆銆涔嬪墠瀛︽暟鎹粨鏋勭殑鏃跺欒嚜宸辯湅涔︺佷篃涓婄綉涓婃煡浜?jiǎn)寰堝璧勬枡锛岃祫鏂欓兘姣旇緝鏁ｃ佽屼笖鎻忚堪鐨勪笉鏄緢娓呮錛屽浜庡綋鏃跺垰鍒?/p>
鎺ヨЕ綆楁硶鐨勬垜錛岃瀹屽叏鐞嗚В榪樻槸鏈変竴瀹氶毦搴︺備粖澶╁垰濂芥湁鏃墮棿灝辨暣鐞嗕簡(jiǎn)涓嬫濊礬銆侀噸鍐欏垎鏋愪簡(jiǎn)涓涓嬩箣鍓嶇殑鐤戞儜鐨勫湴鏂廣?/p>
娌℃湁閫忓交鐨勫湴鏂逛究閮借眮鐒跺紑鏈椾簡(jiǎn)銆傛墍浠ヨ揩涓嶅強(qiáng)寰呮妸鎴戠殑鎯蟲(chóng)硶璁板綍涓嬫潵錛屽拰澶у鍒嗕韓銆?/p>
銆銆濡傛灉浣犱篃鏄拰涔嬪墠鐨勬垜涓鏍峰hanoi tower娌¤兘瀹屽叏娑堝寲錛屾垨鑰呭垰鍒氭帴瑙︽眽璇哄錛岄偅甯屾湜鎴戠殑榪欑鐞嗚В鏂瑰紡鑳界粰浣犱簺
璁稿府鍔╋紝濡傛灉浣犺寰楀凡緇忓畬鍏ㄦ帉鎻＄殑姣旇緝鐗㈤潬浜?jiǎn)锛岄偅涔熷彲浠ョ湅鐪嬪Q屾湁濂界殑idea鍙互涓璧峰垎浜紱姣曠珶浜ゆ祦璁ㄨ涔熸槸涓縐嶅緢濂界殑
瀛︿範(fàn)鏂瑰紡銆?/p>
銆銆濂戒簡(jiǎn)錛屽簾璇濅笉澶氳錛屽垏鍏ユ棰樸?/p>
鍏充簬姹夎濉旇搗婧愬晩銆佷紶璇村晩紲為┈鐨勫氨涓嶅暟鍡︿簡(jiǎn)錛屾垜浠洿鎺ュ垏鍏ユ棰橈細(xì)
闂鎻忚堪錛?/p>
銆銆鏈変竴涓⒌濉旓紝濉斿唴鏈変笁涓駭A銆丅銆丆錛孉搴т笂鏈夎騫蹭釜鐩樺瓙錛岀洏瀛愬ぇ灝忎笉絳夛紝澶х殑鍦ㄤ笅錛屽皬鐨勫湪涓婏紙濡傚浘錛夈?/p>
鎶婅繖浜涗釜鐩樺瓙浠嶢搴хЩ鍒癈搴э紝涓棿鍙互鍊熺敤B搴т絾姣忔鍙兘鍏佽縐誨姩涓涓洏瀛愶紝騫朵笖鍦ㄧЩ鍔ㄨ繃紼嬩腑錛?涓駭涓婄殑鐩?/p>
瀛愬緇堜繚鎸佸ぇ鐩樺湪涓嬶紝灝忕洏鍦ㄤ笂銆?/p>
鎻忚堪綆鍖栵細(xì)鎶夾鏌變笂鐨刵涓洏瀛愮Щ鍔ㄥ埌C鏌憋紝鍏朵腑鍙互鍊熺敤B鏌便?/p>
銆銆
銆銆鎴戜滑鐩存帴鍋囪鏈塶涓洏瀛愶細(xì)
銆銆鍏堟妸鐩樺瓙浠庡皬鍒板ぇ鏍囪涓?銆?銆?......n
銆銆鍏堢湅鍘熼棶棰樹(shù)笁涓煴瀛愮殑鐘舵侊細(xì)
鐘舵?銆銆A錛氭寜欏哄簭鍫嗘斁鐨刵涓洏瀛愩侭:絀虹殑銆侰錛氱┖鐨勩?/span>
銆銆鐩爣鏄鎶夾涓婄殑n涓洏瀛愮Щ鍔ㄥ埌C銆傚洜涓哄繀欏誨ぇ鐨勫湪涓嬪皬鐨勫湪涓婏紝鎵浠ユ渶緇堢粨鏋淐鐩樹(shù)笂鏈涓嬮潰鐨勫簲璇ユ槸鏍囧彿涓簄鐨勭洏瀛愶紝璇曟兂錛?/p>
瑕佸彇寰桝涓婄殑絎琻涓洏瀛愶紝灝辮鎶婂畠涓婇潰鐨刵-1涓洏瀛愭嬁寮鍚э紵鎷垮紑鏀懼湪鍝噷鍛紵鍏辨湁涓変釜鏌卞瓙錛欰鏄劇劧涓嶆槸銆佸鏋滄斁鍦–涓?/p>
浜?jiǎn)锛岄偅涔堟渶澶х殑鐩樺瓙灝辨病鍦版柟鏀撅紝闂榪樻槸娌″緱鍒拌В鍐熾傛墍浠ラ夋嫨B鏌便傚綋鐒?dòng)灱孊涓婇潰涔熸槸鎸夌収澶у湪涓嬪皬鍦ㄤ笂鐨勫師鍒欏爢鏀劇殑
錛堣浣忥細(xì)鍏堜笉瑕佺鍏蜂綋濡備綍縐誨姩錛屽彲浠ョ湅鎴愮敤涓涓嚱鏁板畬鎴愮Щ鍔紝鐜板湪涓嶇敤鍘昏冭檻鍑芥暟濡備綍瀹炵幇銆傝繖鐐瑰緢閲嶈錛夈?/strong>
銆銆寰堟槑鏄撅細(xì)涓婁竴姝ュ畬鎴愬悗涓変釜濉旂殑鐘舵侊細(xì)
鐘舵?錛?nbsp;銆銆A錛氬彧鏈夋渶澶х殑涓涓洏瀛愩侭錛氭湁鎸夎鍒欏爢鏀劇殑n-1涓洏瀛愩侰絀虹殑銆?/span>
銆銆涓婇潰鐨勫緢濂界悊瑙ｅ惂錛屽ソ錛屽叾瀹炲埌榪欓噷灝卞凡緇忓畬鎴愪竴鍗婁簡(jiǎn)銆傦紙濡傛灉鍓嶉潰鐨勬病鎳傦紝璇烽噸鐪嬩竴閬嶃俻oint錛氫笉瑕佺濡備綍縐誨姩錛侊級(jí)
鎴戜滑緇х畫(huà)錛?/p>
銆銆榪欐椂鍊欙紝鍙互鐩存帴鎶夾涓婄殑鏈澶х洏縐誨姩鍒癈鐩橈紝縐誨姩鍚庣殑鐘舵侊細(xì)
涓棿鐘舵侊細(xì)銆銆A錛氱┖鐨勩侭錛歯-1涓洏瀛愩侰錛氭湁涓涓渶澶х洏錛堢n涓洏瀛愶級(jí)
銆銆瑕佹敞鎰忕殑涓鐐規(guī)槸錛氳繖鏃跺欑殑C鏌卞叾瀹炲彲浠ョ湅鍋氭槸絀虹殑銆傚洜涓哄墿涓嬬殑鎵鏈夌洏瀛愰兘姣斿畠?yōu)畯锛屽畠浠腑鐨勪恢M綍涓涓兘鍙互鏀懼湪涓婇潰錛屼篃灝辨槸銆銆銆銆銆銆 銆銆銆銆銆銆銆銆 C鏌變笂銆?/p>
銆銆鎵浠ョ幇鍦ㄤ笁涓煴瀛愮殑鐘舵侊細(xì)
涓棿鐘舵侊細(xì)銆銆A錛氱┖鐨勩侭錛歯-1涓洏瀛愩侰錛氱┖鐨?/span>
銆銆鎯充竴鎯籌紝鐜板湪鐨勯棶棰樺拰鍘熼棶棰樻湁浜涚浉浼間箣澶勪簡(jiǎn)鍚э紵銆傘傚浣曟洿鐩鎬技鍛紵銆傛樉鐒?dòng)灱屽彧瑕佸惂B涓婄殑n-1涓洏瀛愮Щ鍔ㄥ埌A錛屽緟瑙ｅ喅鐨勯棶棰樺拰鍘熼棶棰樺氨鐩告瘮灝卞彧鏄妯″彉灝忎簡(jiǎn)
銆銆鐜板湪鑰冭檻濡備綍鎶夿涓婄殑n-1涓洏瀛愮Щ鍔ㄥ埌A涓婏紝鍏跺疄縐誨姩鏂規(guī)硶鍜屼笂鏂囦腑鐨勬妸n-1涓洏?shù)粠A縐誨姩鍒癇鏄竴鏍風(fēng)殑錛屽彧鏄煴瀛愮殑鍚嶇О鎹簡(jiǎn)涓嬭屽凡銆傘傦紙濡傛灉鍐欐垚鍑芥暟錛屽彧鏄弬鏁拌皟鐢ㄩ『搴忔敼鍙樿屽凡錛夈傘
銆銆鍋囪浣犲凡緇忓畬鎴愪笂涓姝ヤ簡(jiǎn)錛堝悓鏍風(fēng)殑錛屼笉瑕佽冭檻濡備綍鍘葷Щ鍔紝鍙鎯崇潃鐢ㄤ竴涓嚱鏁板疄鐜板氨濂斤級(jí)錛岃鐪嬬幇鍦ㄧ殑鐘舵侊細(xì)
鐘舵?錛氥A錛氭湁鎸夐『搴忓爢鏀劇殑n-1涓洏瀛愩侭錛氱┖鐨勩侰錛氭寜欏哄簭鍫嗘斁鐨勭n鐩樺瓙(鍙湅涓虹┖鏌?
灝卞湪鍒氭墠錛屾垜浠畬緹庣殑瀹屾垚浜?jiǎn)涓嬈￠掑綊銆傚鏋滄病鐪嬫噦璇蜂粠鏂扮湅涓閬嶏紝鍙互鐢ㄧ瑪鐢誨嚭涓変釜鐘舵併侀潤(rùn)涓嬪績(jī)鏉ユ參鎱㈡帹鐞嗐?/p>
鎴戜竴鍐嶅己璋冪殑錛氬綋瑕佹妸鏈澶х洏瀛愪笂闈㈢殑鎵鏈夌洏瀛愮Щ鍔ㄥ埌鍙︿竴涓┖鏌變笂鏃訛紝涓嶈鍏沖績(jī)鍏蜂綋濡備綍縐誨姩錛屽彧鐢ㄦ妸瀹冪湅鍋氫竴涓嚱鏁板彲浠ュ畬鎴愬嵆鍙紝涓嶇敤鍏沖績(jī)鍑芥暟鐨勫叿浣撳疄鐜般傚鏋滀綘鐨勬濊礬綰犵粨鍦ㄨ繖閲岋紝灝卞緢闅劇戶(hù)緇繁鍏ヤ簡(jiǎn)銆?/em>
鍒拌繖閲岋紝鍏跺疄 鍩烘湰鎬濊礬宸茬粡鐞嗘竻浜?jiǎn)銆傜姸鎬?鍜岀姸鎬?錛岄櫎浜?jiǎn)瑙勬ā鍙槥?錛屽叾瀹冩柟闈㈡病鏈変換浣曞尯鍒簡(jiǎn)銆傜劧鍚庡彧瑕佺敤鐩稿悓鐨勬濈淮鏂瑰紡錛屽氨鑳藉線(xiàn)涓嬫繁鍏ャ傘傘?/p>
濂戒簡(jiǎn)錛岀湅鐪嬪浣曠敤綆楁硶瀹炵幇鍚э細(xì)
瀹氫箟鍑芥暟Hanoi錛坅,b,c,n錛夎〃紺烘妸a涓婄殑n涓洏瀛愮Щ鍔ㄥ埌c涓婏紝鍏朵腑鍙互鐢ㄥ埌b銆?/p>
瀹氫箟鍑芥暟move(m,n)琛ㄧず鎶妋涓婄殑鐩樺瓙縐誨姩鍒皀涓?/p>
鎴戜滑闇瑕佽В鍐崇殑闂姝ｆ槸銆銆Hanoi (a,b,c,n) 銆銆//涓婃枃涓殑鐘舵?
1銆佹妸A涓婄殑n-1涓Щ鍔ㄥ埌B錛?nbsp; 銆銆Hanoi (a,c,b,n-1); // 鎿嶄綔緇撴潫涓虹姸鎬?
2銆佹妸A涓婄殑澶х洏瀛愮Щ鍔ㄥ埌C move(a,c)銆銆銆銆
3銆佹妸B涓婄殑n-1縐誨姩鍒癆銆銆銆銆銆Hanoi (b,c,a,n-1);銆銆//鎿嶄綔緇撴潫浣嶇姸鎬?(鍜岀姸鎬?鐩告瘮鍙槸瑙勬ā鍙樺皬)
濡傛灉鐜板湪榪樹(shù)笉鑳界悊瑙ｃ佽鍥炶繃澶村啀鐪嬩竴閬嶃佹瘯绔熷鏋滄槸鍒濆鑰呬笉鏄緢瀹規(guī)槗灝辮兘鐞嗚В鐨勩傚彲浠ョ敤絎旇涓嬪嚑涓叧閿殑鐘舵侊紝騫朵笖鐪嬬湅浣犳湁娌℃湁鐪熸鐨勬姇鍏ュ幓鐪嬶紝鐙珛鍘繪濊冧簡(jiǎn)銆?/span>
import java.io.IOException;
import java.io.InputStreamReader;
public class Hanoi {
public static void main(String[] args) throws IOException{
int n;
BufferedReader buf;
buf = new BufferedReader(new InputStreamReader(System.in));
System.out.println("Please input the number of disk ");
n = Integer.parseInt(buf.readLine());
Hanoi hanoi = new Hanoi();
hanoi.move(n,'A','B','C');
}
public void move(int n, char a, char b, char c){
if(n == 1){
System.out.println("Disk " + n + " From " + a + " To " + c);
}
else{
move(n-1,a,c,b);
System.out.println("Disk " + n + " From " + a + " To " + c);
move(n-1,b,a,c);
}
}
}
浠ヤ笂銆佸鏋滄湁涓嶅鐨勫湴鏂廣佽繕甯屾湜鎮(zhèn)ㄨ兘鎸囧嚭銆?/p>
鎴戝閫掑綊鐨勪竴鐐圭悊瑙ｏ細(xì)
瑙ｅ喅瀹為檯闂鏃躲佷笉鑳藉お鍘誨叧蹇?jī)瀹炵幇鐨劸l嗚妭錛堝洜涓洪掑綊鐨勮繃紼嬫伆鎭版槸鎴戜滑瀹炵幇鐨勬柟娉曪級(jí)灝卞儚榪欎釜闂錛屽鍦ㄧ涓姝ュ氨榪囧鐨勭籂緇撲簬濡備綍鎶妌-1涓洏瀛愮Щ鍔ㄥ埌B涓娿侀偅涔堜綘鐨勬濊礬灝卞緢闅劇戶(hù)緇繁鍏ャ傚彧瑕佺湅鍋氭槸鐢ㄥ嚱鏁板疄鐜板氨濂斤紝濡傛灉浣犺兘鐪嬪嚭涓嶇鎬庝箞縐誨姩錛屽叾瀹炴湰璐ㄩ兘涓鏍風(fēng)殑鏃跺欙紝閭ｄ箞灝辮兘杈冨揩鐨勫緱鍒扮粨鏋滀簡(jiǎn)銆傚氨鍍忚繖涓渚嬶紝瑕佹敞鎰忓埌鎴戜滑鍋氱殑鍏抽敭鍑犳閮藉彧鏄Щ鍔ㄧ殑欏哄簭鏈夋敼鍙橈紝鍏朵腑鐨勮鍒欐病鏈夋敼鍙橈紝濡?/p>
濡傛灉鐢ㄥ嚱鏁拌〃紺虹殑璇濓紝灝卞彧鏄弬鏁拌皟鐢ㄧ殑欏哄簭鏈夋墍涓嶅悓浜?jiǎn)銆傚湪閫掑綊鐨勮繍鐢ㄤ腑銆佷笉鐢ㄥ叧蹇?jī)姣忎竴姝ョ殑鍏蜂綋瀹炵幇 錛屽彧瑕佺湅鍋氱敤涓涓嚱鏁拌〃紺哄氨濂姐傚垎鏋愰棶棰樼殑鏃跺欙紝鏈濂界敾鍑?guó)檱忿q殑鎺ㄧ悊榪囩▼錛屽緱鍒版湁鏁堢殑鐘舵佸浘銆?/p>
鎬濊冮棶棰樿姹傛濊礬鐨勮繛璐с佸姏姹傚敖蹇繘鍏ョ姸鎬侊紝浜彈瀹屽叏鎶曞叆鍒頒竴浠朵簨涓殑緹庡鎰熻
]]>
http://renaud.waldura.com/doc/java/dijkstra/
Dijkstra's algorithm is probably the best-known and thus most implemented shortest path algorithm. It is simple, easy to understand and implement, yet impressively efficient. By getting familiar with such a sharp tool, a developer can solve efficiently and elegantly problems that would be considered impossibly hard otherwise. Be my guest as I explore a possible implementation of Dijkstra's shortest path algorithm in Java.
What It Does
Dijkstra's algorithm, when applied to a graph, quickly finds the shortest path from a chosen source to a given destination. (The question "how quickly" is answered later in this article.) In fact, the algorithm is so powerful that it finds all shortest paths from the source to all destinations! This is known as the single-source shortest paths problem. In the process of finding all shortest paths to all destinations, Dijkstra's algorithm will also compute, as a side-effect if you will, a spanning tree for the graph. While an interesting result in itself, the spanning tree for a graph can be found using lighter (more efficient) methods than Dijkstra's.
How It Works
First let's start by defining the entities we use. The graph is made of vertices (or nodes, I'll use both words interchangeably), and edges which link vertices together. Edges are directed and have an associated distance, sometimes called the weight or the cost. The distance between the vertex u and the vertex v is noted [u, v] and is always positive.
Dijkstra's algorithm partitions vertices in two distinct sets, the set of unsettled vertices and the set of settled vertices. Initially all vertices are unsettled, and the algorithm ends once all vertices are in the settled set. A vertex is considered settled, and moved from the unsettled set to the settled set, once its shortest distance from the source has been found.
We all know that algorithm + data structures = programs, in the famous words of Niklaus Wirth. The following data structures are used for this algorithm:
| d | stores the best estimate of the shortest distance from the source to each vertex |
|---|---|
| π | stores the predecessor of each vertex on the shortest path from the source |
| S | the set of settled vertices, the vertices whose shortest distances from the source have been found |
| Q | the set of unsettled vertices |
With those definitions in place, a high-level description of the algorithm is deceptively simple. With s as the source vertex:
while Q is not empty {
u = extract-minimum(Q)
add u to S
relax-neighbors(u)
}
Dead simple isn't it? The two procedures called from the main loop are defined below:
for each vertex v adjacent to u, v not in S
{
if d(v) > d(u) + [u,v]
// a shorter distance exists
{
d(v) = d(u) + [u,v]
π(v) = u
add v to Q
}
}
}
extract-minimum(Q) {
find the smallest (as defined by d) vertex in Q
remove it from Q and return it
}
An Example
So far I've listed the instructions that make up the algorithm. But to really understand it, let's follow the algorithm on an example. We shall run Dikjstra's shortest path algorithm on the following graph, starting at the source vertex a.
We start off by adding our source vertex a to the set Q. Q isn't empty, we extract its minimum, a again. We add a to S, then relax its neighbors. (I recommend you follow the algorithm in parallel with this explanation.)
Those neighbors, vertices adjacent to a, are b and c (in green above). We first compute the best distance estimate from a to b. d(b) was initialized to infinity, therefore we do:
d(b) = d(a) + [a,b] = 0 + 4 = 4π(b) is set to a, and we add b to Q. Similarily for c, we assign d(c) to 2, and π(c) to a. Nothing tremendously exciting so far.
The second time around, Q contains b and c. As seen above, c is the vertex with the current shortest distance of 2. It is extracted from the queue and added to S, the set of settled nodes. We then relax the neighbors of c, which are b, d and a.
a is ignored because it is found in the settled set. But it gets interesting: the first pass of the algorithm had concluded that the shortest path from a to b was direct. Looking at c's neighbor b, we realize that:
d(b) = 4 > d(c) + [c,b] = 2 + 1 = 3Ah-ah! We have found that a shorter path going through c exists between a and b. d(b) is updated to 3, and π(b) updated to c. b is added again to Q. The next adjacent vertex is d, which we haven't seen yet. d(d) is set to 7 and π(d) to c.
The unsettled vertex with the shortest distance is extracted from the queue, it is now b. We add it to the settled set and relax its neighbors c and d.
We skip c, it has already been settled. But a shorter path is found for d:
d(d) = 7 > d(b) + [b,d] = 3 + 1 = 4Therefore we update d(d) to 4 and π(d) to b. We add d to the Q set.
At this point the only vertex left in the unsettled set is d, and all its neighbors are settled. The algorithm ends. The final results are displayed in red below:
- π - the shortest path, in predecessor fashion
- d - the shortest distance from the source for each vertex
This completes our description of Dijkstra's shortest path algorithm. Other shortest path algorithms exist (see the References section at the end of this article), but Dijkstra's is one of the simplest, while still offering good performance in most cases.
Implementing It in Java
The Java implementation is quite close to the high-level description we just walked through. For the purpose of this article, my Java implementation of Dijkstra's shortest path finds shortest routes between cities on a map. The RoutesMap object defines a weighted, oriented graph as defined in the introduction section of this article.
int getDistance(City start, City end);
List<City> getDestinations(City city);
}
Data Structures
We've listed above the data structures used by the algorithm, let's now decide how we are going to implement them in Java.
S, the settled nodes set
This one is quite straightforward. The Java Collections feature the Set interface, and more precisely, the HashSet implementation which offers constant-time performance on the contains operation, the only one we need. This defines our first data structure.
private boolean isSettled(City v) {
return settledNodes.contains(v);
}
Notice how my data structure is declared as an abstract type (Set) instead of a concrete type (HashSet). Doing so is a good software engineering practice, as it allows to change the actual type of the collection without any modification to the code that uses it.
d, the shortest distances list
As we've seen, one output of Dijkstra's algorithm is a list of shortest distances from the source node to all the other nodes in the graph. A straightforward way to implement this in Java is with a Map, used to keep the shortest distance value for every node. We also define two accessors for readability, and to encapsulate the default infinite distance.
private void setShortestDistance(City city, int distance) {
shortestDistances.put(city, distance);
}
public int getShortestDistance(City city) {
Integer d = shortestDistances.get(city);
return (d == null) ? INFINITE_DISTANCE : d;
}
You may notice I declare this field final. This is a Java idiom used to flag aggregation relationships between objects. By marking a field final, I am able to convey that it is part of a aggregation relationship, enforced by the properties of final—the encapsulating class cannot exist without this field.
π, the predecessors tree
Another output of the algorithm is the predecessors tree, a tree spanning the graph which yields the actual shortest paths. Because this is the predecessors tree, the shortest paths are actually stored in reverse order, from destination to source. Reversing a given path is easy with Collections.reverse().
The predecessors tree stores a relationship between two nodes, namely a given node's predecessor in the spanning tree. Since this relationship is one-to-one, it is akin to amapping between nodes. Therefore it can be implemented with, again, a Map. We also define a pair of accessors for readability.
private void setPredecessor(City a, City b) {
predecessors.put(a, b);
}
public City getPredecessor(City city) {
return predecessors.get(city);
}
Again I declare my data structure to be of the abstract type Map, instead of the concrete type HashMap. And tag it final as well.
Q, the unsettled nodes set
As seen in the previous section, a data structure central to Dijkstra's algorithm is the set of unsettled vertices Q. In Java programming terms, we need a structure able to store the nodes of our example graph, i.e. City objects. That structure is then looked up for the city with the current shortest distance given by d().
We could do this by using another Set of cities, and sort it according to d() to find the city with shortest distance every time we perform this operation. This isn't complicated, and we could leverage Collections.min() using a custom Comparator to compare the elements according to d().
But because we do this at every iteration, a smarter way would be to keep the set ordered at all times. That way all we need to do to get the city with the lowest distance is to get the first element in the set. New elements would need to be inserted in the right place, so that the set is always kept ordered.
A quick search through the Java collections API yields the PriorityQueue: it can sort elements according to a custom comparator, and provides constant-time access to the smallest element. This is precisely what we need, and we'll write a comparator to order cities (the set elements) according to the current shortest distance. Such a comparator is included below, along with the PriorityQueue definition. Also listed is the small method that extracts the node with the shortest distance.
{
public int compare(City left, City right)
{
int shortestDistanceLeft = getShortestDistance(left);
int shortestDistanceRight = getShortestDistance(right);
if (shortestDistanceLeft > shortestDistanceRight)
{
return +1;
}
else if (shortestDistanceLeft < shortestDistanceRight)
{
return -1;
}
else // equal
{
return left.compareTo(right);
}
}
};
private final PriorityQueue<City> unsettledNodes = new PriorityQueue<City>(INITIAL_CAPACITY, shortestDistanceComparator);
private City extractMin()
{
return unsettledNodes.poll();
}
One important note about the comparator: it is used by the PriorityQueue to determine both object ordering and identity. If the comparator returns that two elements are equal, the queue infers they are the same, and it stores only one instance of the element. To prevent losing nodes with equal shortest distances, we must compare the elements themselves (third block in the if statement above).
Having powerful, flexible data structures at our disposal is what makes Java such an enjoyable language (that, and garbage collection of course).
Putting It All Together
We have defined our data structures, we understand the algorithm, all that remains to do is implement it. As I mentioned earlier, my implementation is close to the high-level description given above. Note that when the only shortest path between two specific nodes is asked, the algorithm can be interrupted as soon as the destination node is reached.
initDijkstra(start);
while (!unsettledNodes.isEmpty()) {
// get the node with the shortest distance
City u = extractMin();
// destination reached, stop
if (u == destination) break;
settledNodes.add(u);
relaxNeighbors(u);
}
}
The DijkstraEngine class implements this algorithm and brings it all together. See "Implementation Notes" below to download the source code.
A Word About Performance
The complexity of Dijkstra's algorithm depends heavily on the complexity of the priority queue Q. If this queue is implemented naively as I first introduced it (i.e. it is re-ordered at every iteration to find the mininum node), the algorithm performs in O(n2), where n is the number of nodes in the graph.
With a real priority queue kept ordered at all times, as we implemented it, the complexity averages O(n log m). The logarithm function stems from the collectionsPriorityQueue class, a heap implementation which performs in log(m).
Implementation Notes
The Java source code discussed in this article is available for download as a ZIP file. Extensive unit tests are provided and validate the correctness of the implementation. Some minimal Javadoc is also provided. As the code makes use of the assert facility and generics, it must be compiled with "javac -source 1.5"; the tests require junit.jar.I warmly recommend Eclipse for all Java development.
I've received a fair amount of e-mail about this article, which has become quite popular. I'm unfortunately unable to answer all your questions, and for this I apologize. Keep in mind this article (and the code) is meant as a starting point: the implementation discussed here is hopefully simple, correct, and relatively easy to understand, but is probably not suited to your specific problem. You must tailor it to your own domain.
My goal in writing this article was to share and teach a useful tool, striving for 1- simplicity and 2- correctness. I purposefully shied away from turning this exercise into a full-blown generic Java implementation. Readers after full-featured, industrial-strength Java implementations of Dijkstra's shortest path algorithm should look at the "Resources" section below.
]]>
APIs.
We define the APIs for bags, queues, and stacks. Beyond the basics, these APIs reflect two Java features: generics and iterable collections.
- Generics. An essential characteristic of collection ADTs is that we should be able to use them for any type of data. A specific Java mechanism known as generics enables this capability. The notation <Item> after the class name in each of our APIs defines the name Item as a type parameter, a symbolic placeholder for some concrete type to be used by the client. You can read Stack<Item> as "stack of items." For example, you can write code such as
to use a stack for String objects.Stack<String> stack = new Stack<String>();
stack.push("Test");
...
String next = stack.pop(); - Autoboxing. Type parameters have to be instantiated as reference types, so Java automatically converts between a primitive type and its corresponding wrapper type in assignments, method arguments, and arithmetic/logic expressions. This conversion enables us to use generics with primitive types, as in the following code:
Automatically casting a primitive type to a wrapper type is known as autoboxing, and automatically casting a wrapper type to a primitive type is known as auto-unboxing.Stack<Integer> stack = new Stack<Integer>(); stack.push(17);
// auto-boxing (int -> Integer) int i = stack.pop();
// auto-unboxing (Integer -> int) - Iterable collections. For many applications, the client's requirement is just to process each of the items in some way, or to iterate through the items in the collection. Java's foreach statement supports this paradigm. For example, suppose that collection is a Queue<Transaction>. Then, if the collection is iterable, the client can print a transaction list with a single statement:
for (Transaction t : collection)
StdOut.println(t); - Bags. A bag is a collection where removing items is not supported—its purpose is to provide clients with the ability to collect items and then to iterate through the collected items. Stats.java is a bag client that reads a sequence of real numbers from standard input and prints out their mean and standard deviation.
- FIFO queues. A FIFO queue is a collection that is based on the first-in-first-out (FIFO) policy. The policy of doing tasks in the same order that they arrive server is one that we encounter frequently in everyday life: from people waiting in line at a theater, to cars waiting in line at a toll booth, to tasks waiting to be serviced by an application on your computer.
- Pushdown stack. A pushdown stack is a collection that is based on the last-in-first-out (LIFO) policy. When you click a hyperlink, your browser displays the new page (and pushes onto a stack). You can keep clicking on hyperlinks to visit new pages, but you can always revisit the previous page by clicking the back button (popping it from the stack). Reverse.java is a stack client that reads a sequence of integers from standard input and prints them in reverse order.
- Arithmetic expression evaluation. Evaluate.java is a stack client that evaluates fully parenthesized arithmetic expressions. It uses Dijkstra's 2-stack algorithm:
- Push operands onto the operand stack.
- Push operators onto the operator stack.
- Ignore left parentheses.
- On encountering a right parenthesis, pop an operator, pop the requisite number of operands, and push onto the operand stack the result of applying that operator to those operands.
This code is a simple example of an interpreter.
Array and resizing array implementations of collections.
- Fixed-capacity stack of strings. FixedCapacityStackOfString.java implements a fixed-capacity stack of strings using an array.
- Fixed-capacity generic stack. FixedCapacityStack.java implements a generic fixed-capacity stack.
- Array resizing stack. ResizingArrayStack.java implements a generic stack using a resizing array. With a resizing array, we dynamically adjust the size of the array so that it is both sufficiently large to hold all of the items and not so large as to waste an excessive amount of space. Wedouble the size of the array in push() if it is full; we halve the size of the array in pop() if it is less than one-quarter full.
- Array resizing queue. ResizingArrayQueue.java implements the queue API with a resizing array.
Linked lists.
A linked list is a recursive data structure that is either empty (null) or a reference to a node having a generic item and a reference to a linked list. To implement a linked list, we start with a nested class that defines the node abstraction
private class Node {
Item item;
Node next;
}
- Building a linked list. To build a linked list that contains the items to, be, and or, we create a Node for each item, set the item field in each of th
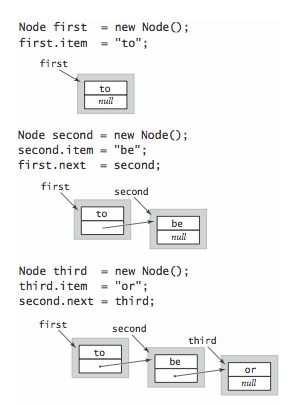
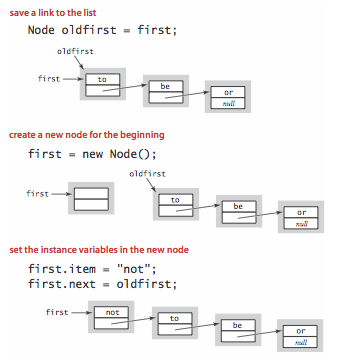
- Insert at the beginning. The easiest place to insert a new node in a linked list is at the beginning.
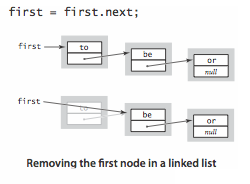
- Remove from the beginning. Removing the first node in a linked list is also easy.
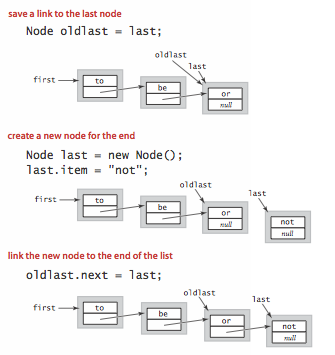
- Insert at the end. To insert a node at the end of a linked list, we maintain a link to the last node in the list.
- Traversal. The following is the idiom for traversing the nodes in a linked list.
for (Node x = first; x != null; x = x.next) {
// process x.item
}
Linked-list implementations of collections.
- Linked list implementation of a stack. Stack.java implements a generic stack using a linked list. It maintains the stack as a linked list, with the top of the stack at the beginning, referenced by an instance variable first. To push() an item, we add it to the beginning of the list; to pop()an item, we remove it from the beginning of the list.
- Linked list implementation of a queue. Program Queue.java implements a generic FIFO queue using a linked list. It maintains the queue as a linked list in order from least recently to most recently added items, with the beginning of the queue referenced by an instance variable firstand the end of the queue referenced by an instance variable last. To enqueue() an item, we add it to the end of the list; to dequeue() an item, we remove it from the beginning of the list.
- Linked list implementation of a bag. Program Bag.java implements a generic bag using a linked list. The implementation is the same as Stack.javaexcept for changing the name of push() to add() and removing pop().
Iteration.
To consider the task of implementing iteration, we start with a snippet of client code that prints all of the items in a collection of strings, one per line:This foreach statement is shorthand for the following while statement:
...
for (String s : collection)
StdOut.println(s);
...
To implement iteration in a collection:
while (i.hasNext()) {
String s = i.next();
StdOut.println(s);
}
- Include the following import statement so that our code can refer to Java's java.util.Iterator interface:
import java.util.Iterator;
- Add the following to the class declaration, a promise to provide an iterator() method, as specified in the java.lang.Iterable interface:
implements Iterable<Item>
- Implement a method iterator() that returns an object from a class that implements the Iterator interface:
public Iterator<Item> iterator() {
return new ListIterator();
} - Implement a nested class that implements the Iterator interface by including the methods hasNext(), next(), and remove(). We always use an empty method for the optional remove() method because interleaving iteration with operations that modify the data structure is best avoided.
- The nested class ListIterator in Bag.java illustrates how to implement a class that implements the Iterator interface when the underlying data structure is a linked list.
- The nested class ArrayIterator in ArrayResizingBag.java does the same when the underlying data structure is an array.
Autoboxing Q + A
Q. How does auto-boxing handle the following code fragment?
A. It results in a run-time error. Primitive type can store every value of their corresponding wrapper type except null.
Q. Why does the first group of statements print true, but the second false?
Integer a2 = 100;
System.out.println(a1 == a2);
// true Integer b1 = new Integer(100);
Integer b2 = new Integer(100);
System.out.println(b1 == b2);
// false Integer c1 = 150;
Integer c2 = 150;
System.out.println(c1 == c2);
// false
A. The second prints false because b1 and b2 are references to different Integer objects. The first and third code fragments rely on autoboxing. Surprisingly the first prints true because values between -128 and 127 appear to refer to the same immutable Integer objects (Java's implementation of valueOf() retrieves a cached values if the integer is between -128 and 127), while Java constructs new objects for each integer outside this range.
Here is another Autoboxing.java anomaly.
Generics Q + A
Q. Are generics solely for auto-casting?
A. No, but we will use them only for "concrete parameterized types", where each data type is parameterized by a single type. The primary benefit is to discover type mismatch errors at compile-time instead of run-time. There are other more general (and more complicated) uses of generics, including wildcards. This generality is useful for handling subtypes and inheritance. For more information, see this Generics FAQ and this generics tutorial.
Q. Can concrete parameterized types be used in the same way as normal types?
A. Yes, with a few exceptions (array creation, exception handling, with instanceof, and in a class literal).
Q. Why do I get a "can't create an array of generics" error when I try to create an array of generics?
public class ResizingArrayStack<Item> {
Item[] a = new Item[1];
}
A. Unfortunately, creating arrays of generics is not possible in Java 1.5. The underlying cause is that arrays in Java are covariant, but generics are not. In other words, String[] is a subtype of Object[], but Stack<String> is not a subtype of Stack<Object>. To get around this defect, you need to perform an unchecked cast as in ResizingArrayStack.java.
Q. So, why are arrays covariant?
A. Many programmers (and programming language theorists) consider covariant arrays to be a serious defect in Java's type system: they incur unnecessary run-time performance overhead (for example, see ArrayStoreException) and can lead to subtle bugs. Covariant arrays were introduced in Java to circumvent the problem that Java didn't originally include generics in its design, e.g., to implement Arrays.sort(Comparable[]) and have it be callable with an input array of type String[].
Q. Can I create and return a new array of a parameterized type, e.g., to implement a toArray() method for a generic queue?
A. Not easily. You can do it using reflection provided that the client passes an object of the desired concrete type to toArray() This is the (awkward) approach taken by Java's Collection Framework.
]]>
public static int BUFFERSIZE = 2048;
public BufferedReader fbr;
public File originalfile;
private String cache;
private boolean empty;
public BinaryFileBuffer(File f, Charset cs) throws IOException {
originalfile = f;
fbr = new BufferedReader(new InputStreamReader(new FileInputStream(f), cs), BUFFERSIZE);
reload();
}
public boolean empty() {
return empty;
}
private void reload() throws IOException {
try {
if ((this.cache = fbr.readLine()) == null) {
empty = true;
cache = null;
} else {
empty = false;
}
} catch (EOFException oef) {
empty = true;
cache = null;
}
}
public void close() throws IOException {
fbr.close();
}
public String peek() {
if (empty())
return null;
return cache.toString();
}
public String pop() throws IOException {
String answer = peek();
reload();
return answer;
}
}
]]>
]]>